Contents
【問題】
【難易度】★★★☆☆(普通)
次の文章は,マーレ―ループ法に関する記述である。
マーレ―ループ法はケーブル線路の故障点位置を標定するための方法である。
この基本原理は\( \ \fbox { (ア) } \ \)ブリッジに基づいている。図に示すように,ケーブル\( \ \mathrm {A} \ \)の一箇所においてその導体と遮へい層の間に地絡故障を生じているとする。この場合に故障点の位置標定を行うためには,マーレ―ループ装置を接続する箇所の逆側端部において,絶縁破壊を起こしたケーブル\( \ \mathrm {A} \ \)と,これに並行する絶縁破壊を起こしていないケーブル\( \ \mathrm {B} \ \)の\( \ \fbox { (イ) } \ \)どうしを接続して,ブリッジの平衡条件を求める。ケーブル線路長を\( \ L \ \),マーレ―ループ装置を接続した端部側から故障点までの距離を\( \ x \ \),ブリッジの全目盛を\( \ 1000 \ \),ブリッジが平衡したときのケーブル\( \ \mathrm {A} \ \)に接続されたブリッジ端子までの目盛の読みを\( \ a \ \)としたときに,故障点までの距離\( \ x \ \)は\( \ \fbox { (ウ) } \ \)で示される。
なお,この原理上,故障点の地絡抵抗が\( \ \fbox { (エ) } \ \)ことがよい位置標定精度を得るうえで必要である。
ただし,ケーブル\( \ \mathrm {A} \ \),\( \ \mathrm {B} \ \)は同一仕様,かつ,同一長とし,また,マーレ―ループ装置とケーブルの接続線,及びケーブルどうしの接続線のインピーダンスは無視するものとする。
上記の記述中の空白箇所(ア),(イ),(ウ)及び(エ)に当てはまる組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
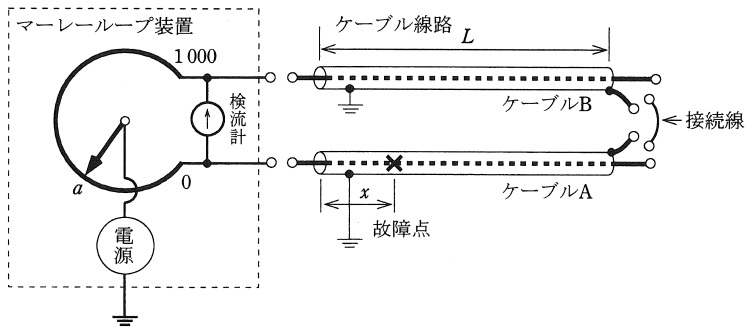
\[
\begin{array}{ccccc}
& (ア) & (イ) & (ウ) & (エ) \\
\hline
(1) & シェーリング & 導 体 & \displaystyle 2L-\frac {aL}{500} & 十分高い \\
\hline
(2) & ホイートストン & 導 体 & \displaystyle \frac {aL}{500} & 十分低い \\
\hline
(3) & ホイートストン & 遮へい層 & \displaystyle \frac {aL}{500} & 十分低い \\
\hline
(4) & シェーリング & 遮へい層 & \displaystyle 2L-\frac {aL}{500} & 十分高い \\
\hline
(5) & ホイートストン & 導 体 & \displaystyle \frac {aL}{500} & 十分高い \\
\hline
\end{array}
\]
【ワンポイント解説】
マーレーループ法は\( \ 2 \ \)種では計算問題として出題されやすい内容ですが,\( \ 3 \ \)種で計算問題が出題されることは少ないかと思います。したがって,故障点位置までの距離は覚えておいても良いかもしれませんが,導出方法を理解している方がより理想的かと思います。
ホイートストンブリッジの平衡条件を利用した方法となります。
1.マーレーループ法
地中送電線は目視にて故障点を標定することが困難なため,マーレーループ法をはじめとした別の方法で故障点を標定します。
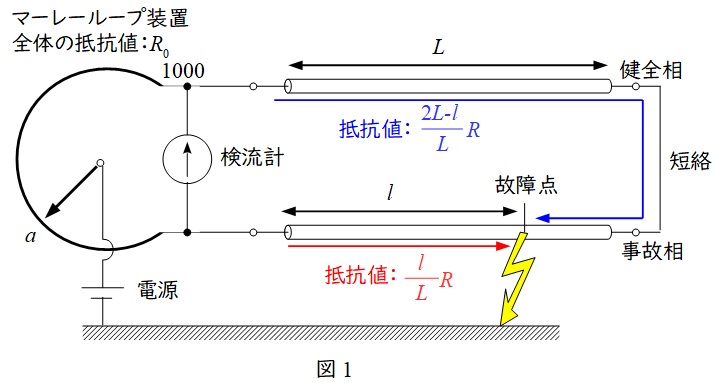
マーレーループ法は図1のように並行した二相の線路において,健全相と故障相の一端をマーレーループ装置に接続し,逆側を短絡します。
電源につなぎ,検流計に電流が流れないようにマーレーループ装置の目盛\( \ a \ \)を調整し,この結果から以下のように求めます。
ケーブル全体の抵抗を\( \ R \ \),長さを\( \ L \ \)とし,故障点までの距離を\( \ l \ \)とすれば,健全相側からの抵抗値は\( \ \displaystyle \frac {2L-l}{L}R \ \),故障相側からの抵抗値は\( \ \displaystyle \frac {l}{L}R \ \)となります。
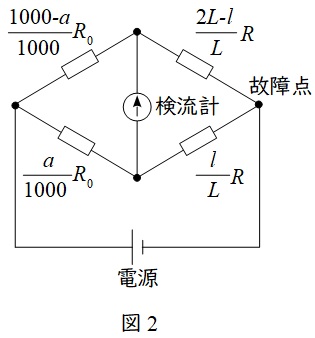
マーレーループ装置の全体の抵抗が\( \ R_{0} \ \),目盛の読みが\( \ a \ \)であるとき,マーレーループ装置の抵抗は\( \ \displaystyle \frac {a}{1000}R_{0} \ \)と\( \ \displaystyle \frac {1000-a}{1000}R_{0} \ \)に分けられ,図2のようなブリッジ回路に変換できることになります。
図2におけるブリッジの平衡条件は,
\[
\begin{eqnarray}
\displaystyle \frac {1000-a}{1000}R_{0}\cdot \frac {l}{L}R &=&\frac {a}{1000}R_{0}\cdot \frac {2L-l}{L}R \\[ 5pt ]
\end{eqnarray}
\]
となるので,これを整理すると,
\[
\begin{eqnarray}
\displaystyle \frac {1000-a}{1000}\cdot \frac {l}{L} &=&\frac {a}{1000}\cdot \frac {2L-l}{L} \\[ 5pt ]
\left( 1000-a\right) l &=&a\left( 2L-l\right) \\[ 5pt ]
1000l -al &=&2aL-al \\[ 5pt ]
1000l &=&2aL \\[ 5pt ]
l &=&\frac {aL}{500} \\[ 5pt ]
\end{eqnarray}
\]
と求められます。
【解答】
解答:(2)
(ア)
マーレーループ法をはじめとするブリッジの平衡条件を利用して抵抗値を求める方法は,ホイートストンブリッジといいます。シェーリングブリッジはコンデンサの静電容量を求めるための方法です。
(イ)
マーレーループ法は導体の故障点を測定する方法なので,導体同士を接続する必要があります。
(ウ)
ワンポイント解説「1.マーレーループ法」と同様に故障点までの距離\( \ x \ \)を求めると,\( \ \displaystyle x=\frac {aL}{500} \ \)と求められます。
(エ)
地絡抵抗は,等価回路上に図示すると図3のようになるため,良い測定精度を得るためには抵抗値は十分に低い方が良いことになります。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは