《電力》〈配電〉[R05下:問13]単相2線式及び単相3線式線路での電力損失に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

単相\( \ 2 \ \)線式及び単相\( \ 3 \ \)線式の線路での電力損失について，次の問に答えよ。

下図のように，単相\( \ 100 \ \mathrm {V} \ \)の抵抗負荷に単相\( \ 2 \ \)線式及び単相\( \ 3 \ \)線式の低圧配電方式で送電する。負荷の総容量は同一であり，\( \ 3 \ \)線式の場合，負荷は図のように線間に均等分割されるものとする。単相\( \ 2 \ \)線式での線路の抵抗損を\( \ 1 \ \)とすると，単相\( \ 3 \ \)線式の線路の抵抗損は\( \ \displaystyle \frac {1}{5} \ \)であった。このとき，単相\( \ 2 \ \)線式での線路の\( \ 1 \ \)線当たりの抵抗に対して，単相\( \ 3 \ \)線式での線路の\( \ 1 \ \)線当たりの抵抗はどのような大きさとなるか。最も近いものを次の(1)～(5)のうちから一つ選べ。

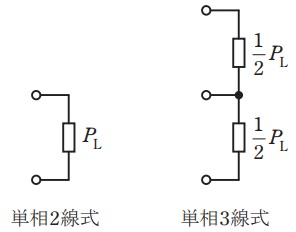
　(1)　\( \ 0.27 \ \)倍　　(2)　\( \ 0.4 \ \)倍　　(3)　\( \ 0.53 \ \)倍　　(4)　\( \ 0.8 \ \)倍　　(5)　\( \ 1.25 \ \)倍

【ワンポイント解説】

単相\( \ 2 \ \)線式及び単相\( \ 3 \ \)線式線路の電力損失の比較に関する問題です。
線路抵抗が異なる条件での比較は今まで少なかったので，迷う受験生も多かったかもしれません。
単相\( \ 3 \ \)線式配電方式の特徴は理解しておくようにしましょう。

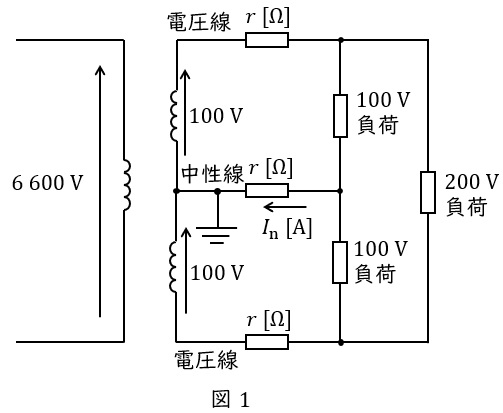
1.単相\( \ 3 \ \)線式配電方式
単相\( \ 3 \ \)線式配電方式は図1のような回路で低圧の需要家に配電する方式で以下のような特徴があります。
・\( \ 100 \ \mathrm {[V]} \ \)負荷と\( \ 200 \ \mathrm {[V]} \ \)負荷の双方に供給可能
・線路負荷が平衡している時，中性点電流\( \ I_{\mathrm {n}} \ \)は零となる
・線路負荷が平衡しており，線間電圧，線電流が等しい場合，単相\( \ 2 \ \)線式に比べ線路電流は\( \ \displaystyle \frac {1}{2} \ \)となるので，線路損失は\( \ \displaystyle \frac {1}{4} \ \)となる

【解答】

解答：(4)
単相\( \ 2 \ \)線式の\( \ 1 \ \)線当たりの抵抗を\( \ r_{2} \ \mathrm {[\Omega ]} \ \)，単相\( \ 3 \ \)線式の\( \ 1 \ \)線当たりの抵抗を\( \ r_{3} \ \mathrm {[\Omega ]} \ \)とする。
単相\( \ 2 \ \)線式及び単相\( \ 3 \ \)線式の負荷電流\( \ I_{2} \ \mathrm {[A]} \ \)及び\( \ I_{3} \ \mathrm {[A]} \ \)の大きさは，
\[
\begin{eqnarray}
I_{2}&=&\frac {P_{\mathrm {L}}}{100} \\[ 5pt ] I_{3}&=&\frac {\displaystyle \frac {1}{2}P_{\mathrm {L}}}{100} \\[ 5pt ] &=&\frac {P_{\mathrm {L}}}{200}=\frac {I_{2}}{2} \\[ 5pt ] \end{eqnarray}
\] であるから，それぞれの線路での電力損失\( \ P_{2} \ \mathrm {[W]} \ \)及び\( \ P_{3} \ \mathrm {[W]} \ \)は，
\[
\begin{eqnarray}
P_{2}&=&2r_{2}{I_{2}}^{2} \\[ 5pt ] P_{3}&=&2r_{3}{I_{3}}^{2} \\[ 5pt ] &=&2r_{3}\left( \frac {I_{2}}{2}\right) ^{2} \\[ 5pt ] &=&\frac {r_{3}{I_{2}}^{2}}{2} \\[ 5pt ] \end{eqnarray}
\] となる。題意より，\( \ \displaystyle P_{3}=\frac {1}{5}P_{2} \ \)の関係があるので，
\[
\begin{eqnarray}
\frac {r_{3}{I_{2}}^{2}}{2}&=&\frac {1}{5}\times 2r_{2}{I_{2}}^{2} \\[ 5pt ] \frac {r_{3}}{2}&=&\frac {2}{5}r_{2} \\[ 5pt ] r_{3}&=&\frac {4}{5}r_{2} \\[ 5pt ] \end{eqnarray}
\] と求められ，単相\( \ 2 \ \)線式での線路の\( \ 1 \ \)線当たりの抵抗に対して，単相\( \ 3 \ \)線式での線路の\( \ 1 \ \)線当たりの抵抗の大きさは\( \ 0.8 \ \)倍であることがわかる。

［別解］
ワンポイント解説「1.単相\( \ 3 \ \)線式配電方式」の通り，線路抵抗が\( \ r_{2} \ \mathrm {[\Omega ]} \ \)で等しいとき，抵抗損は\( \ \displaystyle \frac {1}{4} \ \)となるので，抵抗損が\( \ \displaystyle \frac {1}{5} \ \)となるときの単相\( \ 3 \ \)線式線路の\( \ 1 \ \)線当たりの抵抗\( \ r_{3} \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
5r_{3}{I_{3}}^{2}&=&4r_{2}{I_{3}}^{2} \\[ 5pt ] 5r_{3}&=&4r_{2} \\[ 5pt ] r_{3}&=&\frac {4}{5}r_{2} \\[ 5pt ] \end{eqnarray}
\] となり，単相\( \ 2 \ \)線式での線路の\( \ 1 \ \)線当たりの抵抗に対して，単相\( \ 3 \ \)線式での線路の\( \ 1 \ \)線当たりの抵抗の大きさは\( \ 0.8 \ \)倍であることがわかる。