《法規》〈電気設備技術基準〉[H19:問11]ケーブルの絶縁耐力試験に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

「電気設備技術基準の解釈」に基づいて，最大使用電圧が\( \ 6.9 \ \mathrm {[kV]} \ \)の電路に接続する。導体断面積\( \ 100 \ \mathrm {[{mm}^{2}]} \ \)，長さ\( \ 800 \ \mathrm {[m]} \ \)の高圧\( \ \mathrm {CV} \ \)ケーブル（単心）の絶縁耐力試験を交流で実施する場合について，次の(a)及び(b)に答えよ。
ただし，周波数は\( \ 50 \ \mathrm {[Hz]} \ \)，ケーブルの対地静電容量は\( \ 1 \ \mathrm {[km]} \ \)当たり\( \ 0.45 \ \mathrm {[\mu F]} \ \)とする。

(a)　ケーブルに試験電圧を印加した場合の充電電流\( \ \mathrm {[A]} \ \)の値として，最も近いのは次のうちどれか。

　(1)　\( \ 0.78 \ \)　　(2)　\( \ 1.17 \ \)　　(3)　\( \ 1.46 \ \)　　(4)　\( \ 2.34 \ \)　　(5)　\( \ 3.51 \ \)

(b)　図のような試験回路でケーブルの絶縁耐力試験を行う場合，試験用変圧器の容量を\( \ 5 \ \mathrm {[kV\cdot A]} \ \)としたとき，補償リアクトルの必要最少の設置台数として，正しいのは次のうちどれか。
　ただし，試験電圧を印加したとき，\( \ 1 \ \)台の補償リアクトルに流すことができる電流（電流容量）は\( \ 270 \ \mathrm {[mA]} \ \)とする。

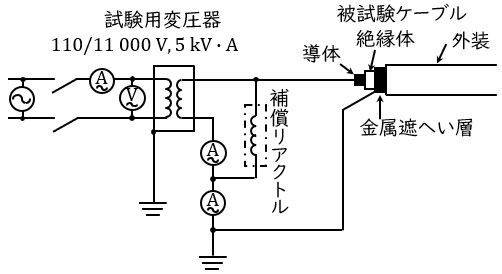
　(1)　\( \ 1 \ \)台 　　(2)　\( \ 2 \ \)台 　　(3)　\( \ 3 \ \)台 　　(4)　\( \ 4 \ \)台 　　(5)　\( \ 5 \ \)台

【ワンポイント解説】

ケーブルの絶縁耐力試験に関する問題です。
ケーブルの絶縁耐力試験は計算パターンがほぼ決まっており，何度も類題が出題されています。最大使用電圧や試験電圧は覚えてしまうぐらいに習熟するようにしましょう。

1.最大使用電圧
最大使用電圧は下表のとおりとなりますが，電験で出題されるのは係数\( \ \displaystyle \frac {1.15}{1.1} \ \)のみです。
＜電気設備の技術基準の解釈第1条(抜粋)＞
\[
\begin{array}{|l|l|}
\hline
　　　　　使用電圧の区分　 & 　　　係数　 \\
\hline
\ 1 \ 000 \ \mathrm {V} \ 以下 & 1.15 \ \\
\hline
\ 1 \ 000 \ \mathrm {V} \ を超え, \ 500 \ 000 \ \mathrm {V} \ 未満　　　　 & 1.15 / 1.1 \\
\hline
\ 500 \ 000 \ \mathrm {V} & 1.05,1.1 \ 又は \ 1.2　　 \\
\hline
\ 1 \ 000 \ 000 \ \mathrm {V} & 1.1 \\
\hline
\end{array}
\]

2.試験電圧
試験電圧は電気設備の技術基準の解釈第15条に細かく規定されています。最初に覚えておくべき内容は交流の試験電圧で，
　　\( \ 1.5 \ \times \ \)最大使用電圧　(最大使用電圧が\( \ 7 \ 000 \ \mathrm {V} \ \)以下の時)
　　\( \ 1.25 \ \times \ \)最大使用電圧　(最大使用電圧が\( \ 7 \ 000 \ \mathrm {V} \ \)を超え\( \ 60 \ 000 \ \mathrm {V} \ \)以下の時)
となります。

3.ケーブル試験時の等価回路
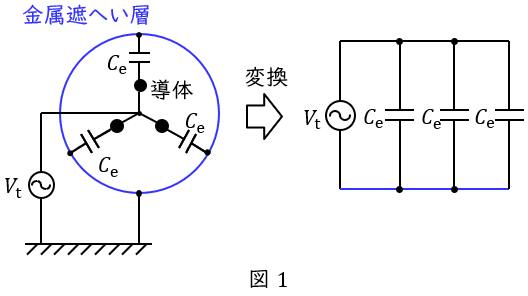
\( \ 1 \ \)線あたりの対地静電容量が\( \ C_{\mathrm {e}} \ \mathrm {[F]} \ \)のケーブルを\( \ 3 \ \)線一括し絶縁耐力試験を行うとき，図1左に示すように各導体間が短絡され，各対地静電容量に試験電圧\( \ V_{\mathrm {t}} \ \mathrm {[V]} \ \)が加わるようになるので，等価回路は図1右のようになります。この等価回路は理解した上で覚えておくと良いでしょう。

【解答】

(a)解答：(2)
長さ\( \ 800 \ \mathrm {[m]} \ \)の\( \ \mathrm {CV} \ \)ケーブルの対地静電容量\( \ C \ \mathrm {[\mu F]} \ \)は，\( \ 1 \ \mathrm {[km]} \ \)当たり\( \ 0.45 \ \mathrm {[\mu F]} \ \)であるから，
\[
\begin{eqnarray}
C &=&0.45\times 0.8 \\[ 5pt ] &=&0.36 \ \mathrm {[\mu F]} \\[ 5pt ] \end{eqnarray}
\] であり，周波数が\( \ f=50 \ \mathrm {[Hz]} \ \)なので，そのリアクタンス\( \ X_{C} \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
X_{C} &=&\frac {1}{2\pi fC}\\[ 5pt ] &=&\frac {1}{2\pi \times 50\times 0.36\times 10^{-6}}\\[ 5pt ] &≒&8 \ 842 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となる。また，最大使用電圧\( \ V_{m}=6.9 \ \mathrm {[kV]} \ \)なので，試験電圧\( \ V_{t} \ \mathrm {[V]} \ \)は，ワンポイント解説「2.試験電圧」の通り，
\[
\begin{eqnarray}
V_{t} &=&1.5 V_{\mathrm {m}} \\[ 5pt ] &=&1.5 \times 6.9 \times 10^{3} \\[ 5pt ] &=&10 \ 350 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となる。よって，試験時の対地充電電流\( \ I_{C} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{C} &=&\frac {V_{t}}{X_{C}} \\[ 5pt ] &=&\frac {10 \ 350}{8 \ 842} \\[ 5pt ] &≒&1.171　→　1.17 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(3)
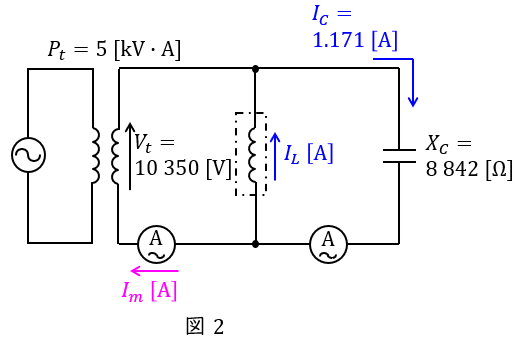
試験用変圧器の容量\( \ P_{t}=5 \ \mathrm {[kV\cdot A]} \ \)とおき，ワンポイント解説「3.ケーブル試験時の等価回路」に沿って等価回路を描くと図2のようになる。

変圧器に流せる最大電流\( \ I_{m} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{m} &=&\frac {P_{t}}{V_{t}} \\[ 5pt ] &=&\frac {5\times 10^{3}}{10 \ 350} \\[ 5pt ] &≒&0.483 \ 1 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となるので，補償リアクトルが補償すべき電流\( \ I_{L} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{L} &=&I_{C}-I_{m} \\[ 5pt ] &=&1.171-0.483 \ 1 \\[ 5pt ] &≒&0.687 \ 9 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となる。\( \ 1 \ \)台の補償リアクトルに流すことができる電流は\( \ 270 \ \mathrm {[mA]} \ \)なので，必要台数\( \ N \ \)は，
\[
\begin{eqnarray}
N &=&\frac {I_{L}}{270\times 10^{-3}} \\[ 5pt ] &=&\frac {0.687 \ 9}{270\times 10^{-3}} \\[ 5pt ] &≒&2.55　→　3 \ \mathrm {[台]} \\[ 5pt ] \end{eqnarray}
\] と求められる。