《法規》〈電気施設管理〉[H23:問11]変圧器の全日効率や日負荷率に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

ある需要家設備において定格容量\( \ 30 \ \mathrm {[kV\cdot A]} \ \)，鉄損\( \ 90 \ \mathrm {[W]} \ \)及び全負荷銅損\( \ 550 \ \mathrm {[W]} \ \)の単相変圧器が設置してある。ある１日の負荷は，
　\( \ 24 \ \mathrm {[kW]} \ \)，力率\( \ 80 \ \mathrm {[％]} \ \)で\( \ 4 \ \)時間
　\( \ 15 \ \mathrm {[kW]} \ \)，力率\( \ 90 \ \mathrm {[％]} \ \)で\( \ 8 \ \)時間
　\( \ 10 \ \mathrm {[kW]} \ \)，力率\( \ 100 \ \mathrm {[％]} \ \)で\( \ 6 \ \)時間
　無負荷で\( \ 6 \ \)時間
であった。この日の変圧器に関して，次の(a)及び(b)の問に答えよ。

(a)　この変圧器の全日効率\( \ \mathrm {[％]} \ \)の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 97.4 \ \)　　(2)　\( \ 97.6 \ \)　　(3)　\( \ 97.8 \ \)　　(4)　\( \ 98.0 \ \)　　(5)　\( \ 98.2 \ \)

(b)　この変圧器の日負荷率\( \ \mathrm {[％]} \ \)の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 38 \ \)　　(2)　\( \ 48 \ \)　　(3)　\( \ 61 \ \)　　(4)　\( \ 69 \ \)　　(5)　\( \ 77 \ \)

【ワンポイント解説】

変圧器の有効利用を模した効率や負荷率に関する問題です。
慣れてしまうと確実に得点できる問題となります。点数差が開きやすい問題となりますので，公式をよく理解して試験本番に臨むようにして下さい。

1.有効電力\( \ P \ \mathrm {[W]} \ \)と無効電力\( \ Q \ \mathrm {[var]} \ \)
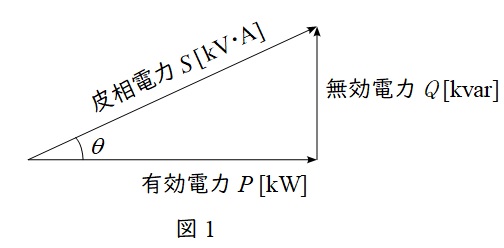
抵抗で消費される電力を有効電力\( \ P \ \mathrm {[W]} \ \)，リアクタンスで消費もしくは供給される電力を無効電力\( \ Q \ \mathrm {[var]} \ \)と呼び，図1のようにベクトル図を描きます。さらに，有効電力\( \ P \ \mathrm {[W]} \ \)と無効電力\( \ Q \ \mathrm {[var]} \ \)のベクトル和は皮相電力\( \ S \ \mathrm {[V\cdot A]} \ \)と呼ばれ，
\[
\begin{eqnarray}
S&=&\sqrt {P^{2}+Q^{2}} \\[ 5pt ] \end{eqnarray}
\] の関係があります。図1において，力率は\( \ \cos \theta \ \)で定義され，
\[
\begin{eqnarray}
\cos \theta &=&\frac {P}{S} \\[ 5pt ] \end{eqnarray}
\] となります。

2.変圧器の効率\( \ \eta \ \)
変圧器の損失は鉄損\( \ p_{\mathrm {i}} \ \mathrm {[W]} \ \)と銅損\( \ p_{\mathrm {c}} \ \mathrm {[W]} \ \)があり，\( \ p_{\mathrm {i}} \ \mathrm {[W]} \ \)は負荷によらず一定であり，\( \ p_{\mathrm {c}} \ \mathrm {[W]} \ \)は負荷(電流)の\( \ 2 \ \)乗に比例します。従って，定格出力\( \ P_{\mathrm {n}} \ \mathrm {[W]} \ \)で利用率\( \ \alpha \ \)の時の変圧器の効率\( \ \eta \ \)は，
\[
\begin{eqnarray}
\eta &=&\frac {出力}{入力} \\[ 5pt ] &=&\frac {出力}{出力+損失} \\[ 5pt ] &=&\frac {\alpha P_{\mathrm {n}}}{\alpha P_{\mathrm {n}}+p_{\mathrm {i}}+\alpha ^{2}p_{\mathrm {c}}} \\[ 5pt ] \end{eqnarray}
\] となります。

3.負荷率の定義
変圧器の負荷率は以下の式で定義されます。
\[
\begin{eqnarray}
負荷率 &=&\frac {平均需要電力}{最大需要電力}\times 100 \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\]

【解答】

(a)解答：(3)
各出力と力率を，
　\( \ P_{\mathrm {1}}=24 \ \mathrm {[kW]} \ \)，\( \ \cos \theta _{\mathrm {1}}=0.8 \ \)
　\( \ P_{\mathrm {2}}=15 \ \mathrm {[kW]} \ \)，\( \ \cos \theta _{\mathrm {2}}=0.9 \ \)
　\( \ P_{\mathrm {3}}=10 \ \mathrm {[kW]} \ \)，\( \ \cos \theta _{\mathrm {2}}=1 \ \)
　\( \ P_{\mathrm {4}}=0 \ \mathrm {[kW]} \ \)
とおく。ワンポイント解説「1.有効電力\( \ P \ \mathrm {[W]} \ \)と無効電力\( \ Q \ \mathrm {[var]} \ \)」の通り，\( \ P_{\mathrm {1}} \ \)，\( \ P_{\mathrm {2}} \ \)，\( \ P_{\mathrm {3}} \ \)の皮相電力\( \ S_{\mathrm {1}} \ \)，\( \ S_{\mathrm {2}} \ \)，\( \ S_{\mathrm {3}} \ \)は，
\[
\begin{eqnarray}
S_{\mathrm {1}} &=&\frac {P_{\mathrm {1}}}{\cos \theta _{\mathrm {1}}} \\[ 5pt ] &=&\frac {24}{0.8} \\[ 5pt ] &=&30 \ \mathrm {[kV\cdot A]} \\[ 5pt ] S_{\mathrm {2}} &=&\frac {P_{\mathrm {2}}}{\cos \theta _{\mathrm {2}}} \\[ 5pt ] &=&\frac {15}{0.9} \\[ 5pt ] &≒&16.67 \ \mathrm {[kV\cdot A]} \\[ 5pt ] S_{\mathrm {3}} &=&\frac {P_{\mathrm {3}}}{\cos \theta _{\mathrm {3}}} \\[ 5pt ] &=&\frac {10}{1} \\[ 5pt ] &=&10 \ \mathrm {[kV\cdot A]} \\[ 5pt ] \end{eqnarray}
\] となる。これと定格容量\( \ S_{\mathrm {n}}=30 \ \mathrm {[kV\cdot A]} \ \)及び全負荷銅損\( \ p_{\mathrm {c}}=550 \ \mathrm {[W]} \ \)より，\( \ P_{\mathrm {1}} \ \)，\( \ P_{\mathrm {2}} \ \)，\( \ P_{\mathrm {3}} \ \)の時の銅損\( \ p_{\mathrm {c1}} \ \)，\( \ p_{\mathrm {c2}} \ \)，\( \ p_{\mathrm {c3}} \ \)は，銅損が負荷の\( \ 2 \ \)乗に比例することから，
\[
\begin{eqnarray}
p_{\mathrm {c1}} &=&\left( \frac {S_{\mathrm {1}}}{S_{\mathrm {n}}}\right) ^{2}p_{\mathrm {c}} \\[ 5pt ] &=&\left( \frac {30}{30}\right) ^{2}\times 550 \\[ 5pt ] &=&550 \ \mathrm {[W]} \\[ 5pt ] p_{\mathrm {c2}} &=&\left( \frac {S_{\mathrm {2}}}{S_{\mathrm {n}}}\right) ^{2}p_{\mathrm {c}} \\[ 5pt ] &=&\left( \frac {16.67}{30}\right) ^{2}\times 550 \\[ 5pt ] &≒&169.8 \ \mathrm {[W]} \\[ 5pt ] p_{\mathrm {c3}} &=&\left( \frac {S_{\mathrm {3}}}{S_{\mathrm {n}}}\right) ^{2}p_{\mathrm {c}} \\[ 5pt ] &=&\left( \frac {10}{30}\right) ^{2}\times 550 \\[ 5pt ] &≒&61.11 \ \mathrm {[W]} \\[ 5pt ] \end{eqnarray}
\] となる。以上より全日効率\( \ \eta \ \mathrm {[％]} \ \)は，
\[
\begin{eqnarray}
\eta &=&\frac {P_{\mathrm {1}}\times 4 +P_{\mathrm {2}}\times 8+P_{\mathrm {3}}\times 6}{\left( P_{\mathrm {1}}\times 4 +P_{\mathrm {2}}\times 8+P_{\mathrm {3}}\times 6\right) +p_{\mathrm {i}}\times 24+\left( p_{\mathrm {c1}}\times 4 +p_{\mathrm {c2}}\times 8+p_{\mathrm {c3}}\times 6\right) }\times 100 \\[ 5pt ] &=&\frac {24\times 10^{3}\times 4 +15\times 10^{3}\times 8+10\times 10^{3}\times 6}{\left( 24\times 10^{3}\times 4 +15\times 10^{3}\times 8+10\times 10^{3}\times 6\right) +90\times 24+\left( 550\times 4 +169.8\times 8+61.11\times 6\right) }\times 100 \\[ 5pt ] &≒&\frac {276000}{276000+2160+3925}\times 100 \\[ 5pt ] &≒&97.8 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(2)
１日の平均需要電力\( \ P_{\mathrm {av}} \ \mathrm {[kW]} \ \)は，
\[
\begin{eqnarray}
P_{\mathrm {av}} &=&\frac {P_{\mathrm {1}}\times 4 +P_{\mathrm {2}}\times 8+P_{\mathrm {3}}\times 6}{24} \\[ 5pt ] &=&\frac {24\times 4 +15\times 8+10\times 6}{24} \\[ 5pt ] &=&11.5 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] であり，最大需要電力は\( \ P_{\mathrm {1}}=24 \ \mathrm {[kW]} \ \)であるから，日負荷率はワンポイント解説「3.負荷率の定義」の通り，
\[
\begin{eqnarray}
負荷率 &=&\frac {P_{\mathrm {av}}}{P_{\mathrm {1}}}\times 100 \mathrm {[％]} \\[ 5pt ] &=&\frac {11.5}{24}\times 100 \mathrm {[％]} \\[ 5pt ] &≒&47.9 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] と求められる。