《機械》〈直流機〉[H18:問1]直流機の磁極を通過する磁束の磁束密度に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

電機子巻線が重ね巻である\( \ 4 \ \)極の直流発電機がある。電機子の全導体数は\( \ 576 \ \)で，磁極の断面積は\( \ 0.025 \ \mathrm {[m^{2} ]} \ \)である。この発電機を回転速度\( \ 600 \ \mathrm {[min^{-1} ]} \ \)で無負荷運転しているとき，端子電圧は\( \ 110 \ \mathrm {[V]} \ \)である。このときの磁極の平均磁束密度\( \ \mathrm {[T]} \ \)の値として，最も近いのは次のうちどれか。

　(1)　\( \ 0.38 \ \)　　(2)　\( \ 0.52 \ \)　　(3)　\( \ 0.64 \ \)　　(4)　\( \ 0.76 \ \)　　(5)　 \( \ 0.88 \ \)

【ワンポイント解説】

誘導起電力を求める公式から，磁極を通過する磁束の磁束密度を求める問題です。
理論科目の電磁気で学習する磁束と磁束密度の関係を忘れてしまうと解けない問題です。
理論科目は基本となりますので，忘れてしまっていたら理論科目のテキストを復習するようにして下さい。

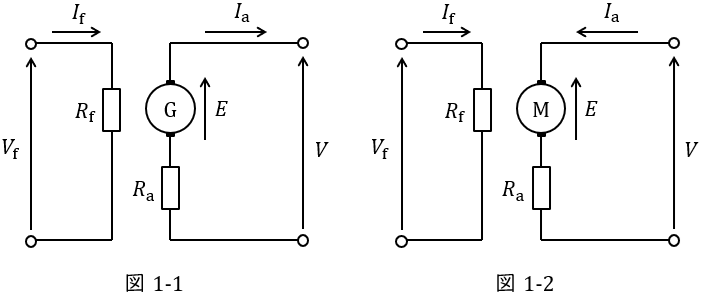
1.他励発電機及び電動機の等価回路
他励発電機の等価回路を図1-1，他励電動機の等価回路を図1-2に示します。ただし，図において，\( \ E \ \mathrm {[V]} \ \)は誘導起電力（電動機の場合は逆起電力），\( \ V \ \mathrm {[V]} \ \)は端子電圧，\( \ I_{\mathrm {a}} \ \mathrm {[A]} \ \)は電機子電流，\( \ I_{\mathrm {f}} \ \mathrm {[A]} \ \)は界磁電流，\( \ R_{\mathrm {a}} \ \mathrm {[\Omega ]} \ \)は電機子抵抗，\( \ R_{\mathrm {f}} \ \mathrm {[\Omega ]} \ \)は界磁抵抗です。
界磁回路が別電源で励磁されているのが特徴です。図を見て分かる通り，発電機も電動機もほぼ同じ等価回路となります。

2.直流機の誘導起電力（逆起電力）\( \ E \ \)
磁極の数\( \ p \ \)，電機子導体数\( \ Z \ \)，電機子巻線並列回路数\( \ a \ \)，各極の磁束\( \ \phi \ \mathrm {[Wb]} \ \)，回転速度\( \ N \ \mathrm {[{min}^{-1}]} \ \)とすると，直流機の誘導起電力（逆起電力）\( \ E \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
E &=&\frac {pZ}{60a}\phi N \\[ 5pt ] &=&k_{\mathrm {e}}\phi N \\[ 5pt ] \end{eqnarray}
\] となり，磁束\( \ \phi \ \mathrm {[Wb]} \ \)と回転速度\( \ N \ \mathrm {[{min}^{-1}]} \ \)に比例します。ただし，波巻の並列回路数は\( \ a=2 \ \)，重ね巻の並列回路数は\( \ a=p \ \)となります。

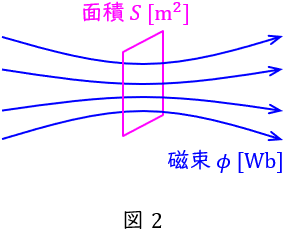
3.鎖交磁束数\( \ \phi \ \)と磁束密度\( \ B \ \)の関係（理論科目）
図2に示すように，面積\( \ S \ \mathrm {[m^{2}]} \ \)のコイルを磁束\( \ \phi \ \mathrm {[Wb]} \ \)が通過しているとき，コイル内の磁束密度\( \ B \ \mathrm {[T]} \ \)は，
\[
\begin{eqnarray}
B&=&\frac {\phi }{S} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(4)
無負荷運転しているとき，電機子電流は零なので，端子電圧と誘導起電力は等しい。したがって，極数\( \ p=4 \ \)，全導体数\( \ Z=576 \ \)，回転速度\( \ N=600 \ \mathrm {[min^{-1} ]} \ \)，並列回路数\( \ a=p=4 \ \)のとき，誘導起電力\( \ E=110 \ \mathrm {[V]} \ \)となるので，このときの\( \ 1 \ \)極あたりの磁束\( \ \phi \ \mathrm {[Wb]} \ \)は，ワンポイント解説「2.直流機の誘導起電力（逆起電力）\( \ E \ \)」の通り，
\[
\begin{eqnarray}
E &=&\frac {pZ}{60a}\phi N \\[ 5pt ] \phi &=&\frac {60aE}{pZN} \\[ 5pt ] &=&\frac {60\times 4\times 110}{4\times 576\times 600} \\[ 5pt ] &≒&0.019 \ 10 \ \mathrm {[Wb]} \\[ 5pt ] \end{eqnarray}
\] となる。磁極の断面積が\( \ S=0.025 \ \mathrm {[m^{2} ]} \ \)なので，磁極の平均磁束密度\( \ B \ \mathrm {[T]} \ \)は，ワンポイント解説「3.鎖交磁束数\( \ \phi \ \)と磁束密度\( \ B \ \)の関係（理論科目）」の通り，
\[
\begin{eqnarray}
B &=&\frac {\phi }{S} \\[ 5pt ] &=&\frac {0.019 \ 10}{0.025} \\[ 5pt ] &=&0.764 \ \mathrm {[T]} \\[ 5pt ] \end{eqnarray}
\] と求められる。