《機械》〈同期機〉[H19:問15]三相同期電動機の角速度とトルクの導出に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

\( \ 6 \ \)極，定格周波数\( \ 60 \ \mathrm {[Hz]} \ \)，電機子巻線が\( \ \mathrm {Y} \ \)結線の円筒形三相同期電動機がある。この電動機の一相当たりの同期リアクタンスは\( \ 3.52 \ \mathrm {[\Omega ]} \ \)であり，また，電機子抵抗は無視できるものとする。端子電圧（線間）\( \ 440 \ \mathrm {[V]} \ \)，定格周波数の電源に接続し，励磁電流を一定に保ってこの電動機を運転したとき，次の(a)及び(b)に答えよ。

(a)　この電動機の同期速度を角速度\( \ \mathrm {[rad / s]} \ \)で表した値として，最も近いのは次のうちどれか。

　(1)　\( \ 12.6 \ \)　　(2)　\( \ 48 \ \)　　(3)　\( \ 63 \ \)　　(4)　\( \ 126 \ \)　　(5)　\( \ 253 \ \)

(b)　無負荷誘導起電力（線間）が\( \ 400 \ \mathrm {[V]} \ \)，負荷角が\( \ 60 \ [^{\circ }] \ \)のとき，この電動機のトルク\( \ \mathrm {[N\cdot m]} \ \)の値として，最も近いのは次のうちどれか。

　(1)　\( \ 115 \ \)　　(2)　\( \ 199 \ \)　　(3)　\( \ 345 \ \)　　(4)　\( \ 597 \ \)　　(5)　\( \ 1 \ 034 \ \)

【ワンポイント解説】

三相同期電動機の角速度とトルクを導出する問題です。
本問のように，同期電動機の等価回路やベクトル図は与えられないことが多いです。
文章を読みながら，等価回路やベクトル図を自力で描けるように準備しておく必要があります。

1.同期電動機の同期速度\( \ N_{\mathrm {s}} \ \)及び同期角速度\( \ \omega _{\mathrm {s}} \ \)
同期電動機の極数が\( \ p \ \)，電源の周波数が\( \ f \ \mathrm {[Hz]} \ \)の時，同期速度\( \ N_{\mathrm {s}} \ \mathrm {[{min}^{-1}]} \ \)は，
\[
\begin{eqnarray}
N_{\mathrm {s}} &=&\frac {120f}{p} \\[ 5pt ] \end{eqnarray}
\] となります。また，同期角速度\( \ \omega _{\mathrm {s}} \ \mathrm {[rad / s]} \ \)は，
\[
\begin{eqnarray}
\omega _{\mathrm {s}} &=&\frac {2\pi N_{\mathrm {s}}}{60} \\[ 5pt ] &=&\frac {2\pi }{60}\cdot \frac {120f}{p} \\[ 5pt ] &=&\frac {4\pi f}{p} \\[ 5pt ] \end{eqnarray}
\] で求められます。

2.三相同期電動機の等価回路及びベクトル図
三相同期電動機の等価回路は，端子電圧\( \ \dot V \ \mathrm {[V]} \ \)（相電圧），誘導起電力\( \ \dot E \ \mathrm {[V]} \ \)（相電圧），電機子電流\( \ \dot I \ \mathrm {[A]} \ \)，同期リアクタンス\( \ x_{\mathrm {s}} \ \mathrm {[\Omega ]} \ \)とすると，図1のようになります。ただし，電機子巻線抵抗は十分に小さいものとします。

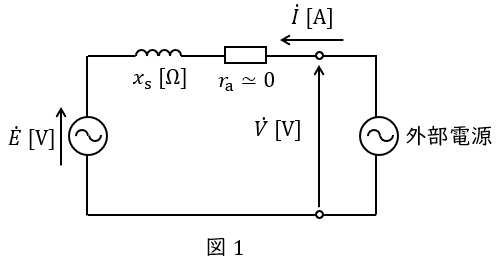
等価回路にキルヒホッフの法則を適用すると，
\[
\begin{eqnarray}
\dot V &=& \dot E+\mathrm {j}x_{\mathrm {s}}\dot I \\[ 5pt ] \end{eqnarray}
\] の関係があることがわかります。
これより，\( \ \dot V \ \mathrm {[V]} \ \)と\( \ \dot I \ \mathrm {[A]} \ \)の力率角を\( \ \theta \ \mathrm {[rad]} \ \)，\( \ \dot V \ \mathrm {[V]} \ \)と\( \ \dot E \ \mathrm {[V]} \ \)の負荷角を\( \ \delta \ \mathrm {[rad]} \ \)とすると，ベクトル図は図2のように描くことができます。

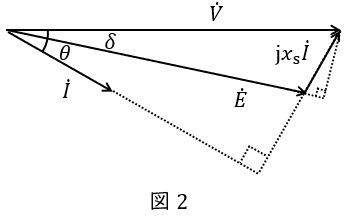
3.同期電動機の出力\( \ P \ \mathrm {[W]} \ \)
図3のベクトル図に示すように，端子電圧\( \ \dot V \ \mathrm {[V]} \ \)（相電圧），誘導起電力\( \ \dot E \ \mathrm {[V]} \ \)（相電圧），電機子電流\( \ \dot I \ \mathrm {[A]} \ \)，\( \ \dot E \ \)と\( \ \dot V \ \)の位相差（負荷角）を\( \ \delta \ \mathrm {[rad]} \ \)，\( \ \dot V \ \)と\( \ \dot I \ \)の位相差（力率角）を\( \ \theta \ \mathrm {[rad]} \ \)とすると，出力\( \ P \ \mathrm {[W]} \ \)は，
\[
\begin{eqnarray}
P &=&3EI\cos \left( \theta -\delta \right) \\[ 5pt ] \end{eqnarray}
\] で求められ，図3の※線を求める式より，
\[
\begin{eqnarray}
x_{\mathrm {s}}I\cos \left( \theta -\delta \right) &=&V\sin \delta \\[ 5pt ] I\cos \left( \theta -\delta \right) &=&\frac {V}{x_{\mathrm {s}}}\sin \delta \\[ 5pt ] \end{eqnarray}
\] となるので，
\[
\begin{eqnarray}
P &=&3EI\cos \left( \theta -\delta \right) \\[ 5pt ] &=&3E\frac {V}{x_{\mathrm {s}}}\sin \delta \\[ 5pt ] &=&\frac {3VE}{x_{\mathrm {s}}}\sin \delta \\[ 5pt ] \end{eqnarray}
\] と求められます。最後の式は公式として覚えておくと良いでしょう。

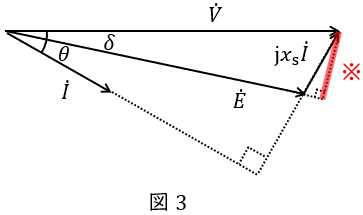
4.同期電動機の出力\( \ P \ \mathrm {[W]} \ \)とトルク\( \ T \ \mathrm {[N\cdot m]} \ \)の関係
同期電動機の出力\( \ P \ \mathrm {[W]} \ \)とトルク\( \ T \ \mathrm {[N\cdot m]} \ \)の関係は，同期角速度\( \ \omega _{\mathrm {s}} \ \mathrm {[rad / s]} \ \)とすると，
\[
\begin{eqnarray}
P &=&\omega _{\mathrm {s}} T \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(a)解答：(4)
極数\( \ p=6 \ \)，定格周波数\( \ f=60 \ \mathrm {[Hz]} \ \)より，同期角速度\( \ \omega _{\mathrm {s}} \ \mathrm {[rad / s]} \ \)は，ワンポイント解説「1.同期電動機の同期速度\( \ N_{\mathrm {s}} \ \)及び同期角速度\( \ \omega _{\mathrm {s}} \ \)」の通り，
\[
\begin{eqnarray}
\omega _{\mathrm {s}}&=&\frac {4\pi f}{p} \\[ 5pt ] &=&\frac {4\pi \times 60}{6} \\[ 5pt ] &≒&125.7　→　126 \ \mathrm {[rad / s]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

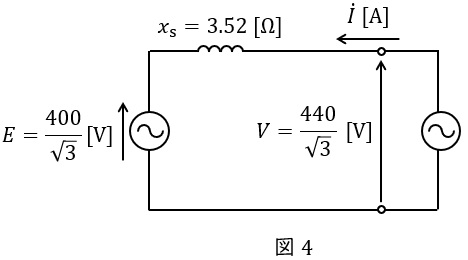
(b)解答：(3)
端子電圧の相電圧\( \ \displaystyle V=\frac {440}{\sqrt {3}} \ \mathrm {[V]} \ \)，無負荷誘導起電力の相電圧\( \ \displaystyle E=\frac {400}{\sqrt {3}} \ \mathrm {[V]} \ \)，一相当たりの同期リアクタンス\( \ x_{\mathrm {s}}=3.52 \ \mathrm {[\Omega ]} \ \)，負荷角\( \ \delta =60 \ [^{\circ }] \ \)なので，等価回路は図4のようになり，出力\( \ P \ \mathrm {[W]} \ \)は，ワンポイント解説「3.同期電動機の出力\( \ P \ \mathrm {[W]} \ \)」の通り，
\[
\begin{eqnarray}
P &=&\frac {3VE}{x_{\mathrm {s}}}\sin \delta \\[ 5pt ] &=&\frac {\displaystyle 3\times \frac {440}{\sqrt {3}}\times \frac {400}{\sqrt {3}}}{3.52}\sin 60 ^{\circ } \\[ 5pt ] &=&\frac {\displaystyle 3\times \frac {440}{\sqrt {3}}\times \frac {400}{\sqrt {3}}}{3.52}\times \frac {\sqrt {3}}{2} \\[ 5pt ] &≒&43 \ 300 \ \mathrm {[W]} \\[ 5pt ] \end{eqnarray}
\] となるので，トルク\( \ T \ \mathrm {[N\cdot m]} \ \)は，ワンポイント解説「4.同期電動機の出力\( \ P \ \mathrm {[W]} \ \)とトルク\( \ T \ \mathrm {[N\cdot m]} \ \)の関係」の通り，
\[
\begin{eqnarray}
T &=&\frac {P}{\omega _{\mathrm {s}}} \\[ 5pt ] &=&\frac {43 \ 300}{125.7} \\[ 5pt ] &≒&344 \ \mathrm {[N\cdot m]} \\[ 5pt ] \end{eqnarray}
\] と求められる。