《機械》〈パワーエレクトロニクス〉[H19:問16]単相双方向サイリスタスイッチに関する計算・論説問題

【問題】

【難易度】★★★★☆（やや難しい）

図は，\( \ 2 \ \)個のサイリスタを逆並列に接続し，位相制御により負荷電力を制御する回路を示す。次の(a)及び(b)に答えよ。

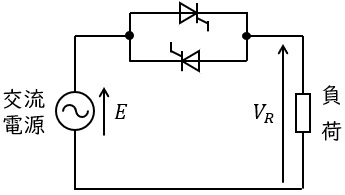
(a)　負荷が抵抗負荷であるとき，制御角\( \ \alpha \ \)が\( \ 90 \ [^{\circ }] \ \)のときの発熱量は，\( \ 30 \ [^{\circ }] \ \)のときの発熱量の何倍か。最も近い値は次のうちどれか。
ただし，負荷の抵抗値は一定とする。また，制御角\( \ \alpha \ \mathrm {[rad]} \ \)のときの負荷電圧の実効値\( \ V_{R} \ \)は，電源電圧の実効値を\( \ E \ \)とすると，\( \ \displaystyle V_{R}=E\cdot \sqrt {1-\frac {\alpha }{\pi }+\frac {\sin 2 \alpha }{2\pi }} \ \)で与えられるものとする。

　(1)　\( \ 0.515 \ \)　　(2)　\( \ 0.717 \ \)　　(3)　\( \ 0.866 \ \)　　(4)　\( \ 0.912 \ \)　　(5)　\( \ 0.986 \ \)

(b)　負荷が抵抗値\( \ R \ \mathrm {[\Omega ]} \ \)，インダクタンス\( \ L \ \mathrm {[H]} \ \)との直列回路からなる誘導性負荷である場合の記述として，誤っているのは次のうちどれか。
ただし，電源の角周波数を\( \ \omega \ \mathrm {[rad / s]} \ \)とし，負荷の基本波力率角を\( \ \displaystyle \phi =\tan ^{-1}⁡ \frac {\omega L}{R} \ \)とする。

　(1)　定常運転時に\( \ \ \alpha ＜\phi \ \)としたとき，サイリスタにオン指令を与えてもサイリスタを毎サイクルターンオン制御できない。

　(2)　負荷が純インダクタンスとみなされる場合は，サイリスタ制御リアクトル方式無効電力補償装置\( \ \left( \mathrm {TCR} \right) \ \)と呼ばれ，図の回路を一相分として，無効電力補償装置に使用される。

　(3)　電流の通流幅は，制御角\( \ \alpha \ \)と基本波力率角\( \ \phi \ \)の関数になる。

　(4)　負荷の基本波力率角（遅れ）が大きくなるほどターンオフ直後のサイリスタに印加される電圧の絶対値は小さくなる。

　(5)　電流高調波成分は，第\( \ 3 \ \)次成分が最も大きい。

【ワンポイント解説】

単相双方向サイリスタスイッチに関する問題です。
(a)は電圧の式が与えられているため標準的な問題と言えますが，(b)はしっかりと動作原理を理解していないと解けない問題なので，難易度としては\( \ 2 \ \)種のパワーエレクトロニクス並みの難易度と言えるでしょう。

1.単相交流電力調整回路の動作
図1-1，図1-2に示す単相交流電力調整回路は以下のように動作します。

①\( \ v_{\mathrm {s}}＞0 \ \)でサイリスタ\( \ \mathrm {Th}_{1} \ \)がオンとなったとき
図1-1のように，電流は交流入力→\( \ \mathrm {Th}_{1} \ \)→負荷→交流入力と流れます。出力電圧\( \ v_{\mathrm {o}} \ \mathrm {[V]} \ \)は素子の電圧降下が無視できるとすると，入力電圧\( \ v_{\mathrm {i}} \ \mathrm {[V]} \ \)と等しくなります。

②\( \ v_{\mathrm {s}}＜0 \ \)でサイリスタ\( \ \mathrm {Th}_{2} \ \)がオンとなったとき
図1-2のように，電流は交流入力→負荷→\( \ \mathrm {Th}_{2} \ \)→交流入力と流れます。出力電圧\( \ v_{\mathrm {o}} \ \mathrm {[V]} \ \)は素子の電圧降下が無視できるとすると，入力電圧\( \ v_{\mathrm {i}} \ \mathrm {[V]} \ \)と等しくなります。

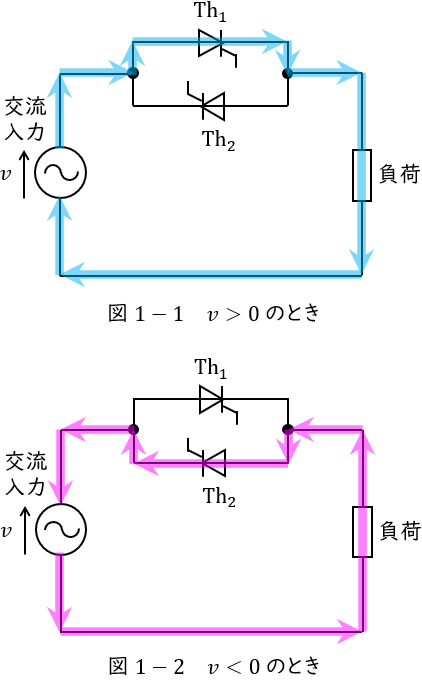
したがって，制御角\( \ \alpha \ \mathrm {[rad]} \ \)でサイリスタをオンさせると，図2のような出力波形となり，制御角を変化させることで，出力電圧を\( \ 0 \ \mathrm {V} \ \)から\( \ v_{\mathrm {i}} \ \mathrm {[V]} \ \)まで調整することができ，そのときの出力電圧の実効値\( \ V_{\mathrm {o}} \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {o}}&=&\sqrt {\frac {1}{\pi }\int _{\alpha }^{\pi }\left( \sqrt {2}V_{\mathrm {i}}\sin \omega t \right) ^{2}\mathrm {d}\omega t} \\[ 5pt ] &=&\sqrt {\frac {2{V_{\mathrm {i}}}^{2}}{\pi }\int _{\alpha }^{\pi }\left( \sin \omega t \right) ^{2}\mathrm {d}\omega t} \\[ 5pt ] &=&V_{\mathrm {i}}\sqrt {\frac {2}{\pi }\int _{\alpha }^{\pi }\frac {1-\cos 2 \omega t}{2}\mathrm {d}\omega t} \\[ 5pt ] &=&V_{\mathrm {i}}\sqrt {\frac {1}{\pi }\int _{\alpha }^{\pi }\left( 1-\cos 2 \omega t\right) \mathrm {d}\omega t} \\[ 5pt ] &=&V_{\mathrm {i}}\sqrt {\frac {1}{\pi }\left[ \omega t-\frac {\sin 2 \omega t}{2}\right] _{\alpha }^{\pi }} \\[ 5pt ] &=&V_{\mathrm {i}}\sqrt {\frac {1}{\pi } \left( \pi -\alpha +\frac {\sin 2 \alpha}{2} \right) } \\[ 5pt ] &=&V_{\mathrm {i}}\sqrt {\frac {\displaystyle \pi -\alpha +\frac {\sin 2 \alpha}{2} }{\pi } } \\[ 5pt ] \end{eqnarray}
\] となります。

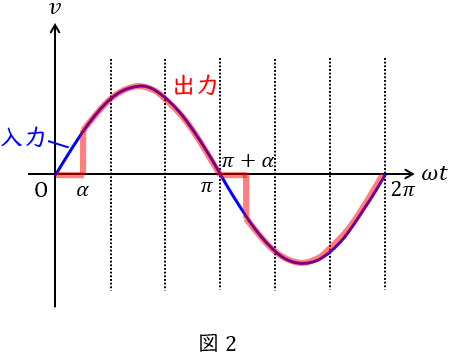
2.負荷が誘導性であるときの単相交流電力調整回路の制御可能範囲
負荷の力率角が\( \ \theta \ \mathrm {[rad]} \ \)であるとき，電流が電圧に対し\( \ \theta \ \mathrm {[rad]} \ \)だけ遅れるため，図3-1や図3-2に示すような波形を描きます。

制御角\( \ \alpha \ \mathrm {[rad]} \ \)が\( \ \alpha ＞ \theta \ \)のとき，図3-1に示すように，\( \ \alpha \ \mathrm {[rad]} \ \)でオンとなったあと，電流が流れはじめ，その後電圧がマイナスとなった後に徐々にリアクトル成分に蓄えられていたエネルギーが放出され電流が零になり，ターンオフとなります。その後\( \ \pi +\alpha \ \mathrm {[rad]} \ \)でオンになり，回路に電流が流れます。したがって，制御可能な範囲となります。
\( \ \alpha ＜ \theta \ \)のとき，図3-2に示すように，仮にサイリスタがオンとなり電流が流れ始めたとしても，\( \ \pi +\alpha \ \mathrm {[rad]} \ \)になってもプラス方向の電流が流れ続けているため，もう一方のサイリスタがオンとなることができません。したがって，制御不可の範囲となります。

【解答】

(a)解答：(1)
制御角\( \ \alpha \ \)が\( \ 90 \ [^{\circ }] \ \)のときの負荷電圧の実効値\( \ V_{R90} \ \)は，
\[
\begin{eqnarray}
V_{R90} &=&E\cdot \sqrt {1-\frac {\displaystyle \frac {\pi }{2}}{\pi }+\frac {\displaystyle \sin \left( 2 \times \frac {\pi }{2}\right) }{2\pi }} \\[ 5pt ] &=&E\cdot \sqrt {1-\frac {1}{2}+\frac {\displaystyle \sin\pi }{2\pi }} \\[ 5pt ] &=&E\cdot \sqrt {1-\frac {1}{2}} \\[ 5pt ] &≒&0.707 \ 1E \\[ 5pt ] \end{eqnarray}
\] となり，制御角\( \ \alpha \ \)が\( \ 30 \ [^{\circ }] \ \)のときの負荷電圧の実効値\( \ V_{R30} \ \)は，
\[
\begin{eqnarray}
V_{R30} &=&E\cdot \sqrt {1-\frac {\displaystyle \frac {\pi }{6}}{\pi }+\frac {\displaystyle \sin \left( 2 \times \frac {\pi }{6}\right) }{2\pi }} \\[ 5pt ] &=&E\cdot \sqrt {1-\frac {1}{6}+\frac {\displaystyle \sin \frac {\pi }{3}}{2\pi }} \\[ 5pt ] &=&E\cdot \sqrt {1-\frac {1}{6}+\frac {\displaystyle \frac {\sqrt {3}}{2}}{2\pi }} \\[ 5pt ] &≒&0.985 \ 5E \\[ 5pt ] \end{eqnarray}
\] となる。よって発熱量の比は，
\[
\begin{eqnarray}
\frac {\displaystyle \frac {{V_{R90}}^{2}}{R}}{\displaystyle \displaystyle \frac {{V_{R30}}^{2}}{R}} &=&\frac {{V_{R90}}^{2}}{{V_{R30}}^{2}} \\[ 5pt ] &=&\frac {\left( 0.707 \ 1E\right) ^{2}}{\left( 0.985 \ 5E\right) ^{2}} \\[ 5pt ] &≒&0.515 \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(4)
(1)正しい
ワンポイント解説「2.負荷が誘導性であるときの単相交流電力調整回路の制御可能範囲」の通り，\( \ \ \alpha ＜\phi \ \)としたときは，サイリスタにオン指令を与えてもサイリスタを毎サイクルターンオン制御できません。

(2)正しい
問題文の通り，負荷が純インダクタンスとみなされる場合は，サイリスタ制御リアクトル方式無効電力補償装置\( \ \left( \mathrm {TCR} \right) \ \)と呼ばれ，無効電力補償装置に使用されます。

(3)正しい
ワンポイント解説「2.負荷が誘導性であるときの単相交流電力調整回路の制御可能範囲」図3-1の通り，電流の通流幅は制御角\( \ \alpha \ \)と基本波力率角\( \ \phi \ \)の関数となります。

(4)誤り
図2及び図3-1に示すように，力率\( \ 1 \ \)の場合にはターンオフ時のサイリスタに印加される電圧は\( \ 0 \ \)となりますが，遅れ力率の場合にはターンオフ時にサイリスタに印加される電圧は\( \ 0 \ \)より大きくなります。

(5)正しい
問題文の通り，図3-1のような波形が得られるとき，電流の高調波は第\( \ 3 \ \)次成分が最も大きくなります。