《機械》〈自動制御〉[H19:問17]抵抗とコンデンサを組み合わせた回路の周波数伝達関数に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

図1及び図2について，次の(a)及び(b)に答えよ。

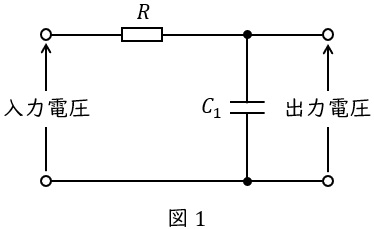
(a)　図1は，抵抗\( \ R \ \mathrm {[\Omega ]} \ \)と静電容量\( \ C_{1} \ \mathrm {[F]} \ \)による一次遅れ要素の回路を示す。この回路の入力電圧に対する出力電圧の周波数伝達関数を\( \ \displaystyle G(j\omega )=\frac {1}{1+j\omega T_{1}} \ \)として表したとき，\( \ T_{1} \ \mathrm {[s]} \ \)を示す式として，正しいのは次のうちどれか。
ただし，入力電圧の角周波数は\( \ \omega \ \mathrm {[rad / s]} \ \)である。

　(1)　\( \ \displaystyle T_{1}=\frac {1}{C_{1}R} \ \)　　(2)　\( \ \displaystyle T_{1}=C_{1}R \ \)　　(3)　\( \ \displaystyle T_{1}=1+C_{1}R \ \)　
　(4)　\( \ \displaystyle T_{1}=\frac {1+C_{1}R}{C_{1}R} \ \)　　(5)　\( \ \displaystyle T_{1}=\frac {C_{1}}{1+C_{1}R} \ \)

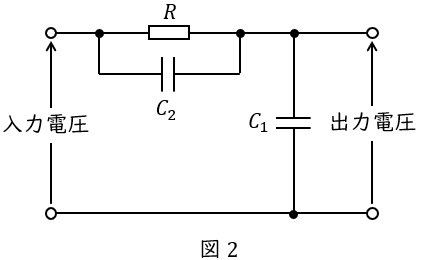
(b)　図2は，図1の回路の過渡応答を改善するために静電容量\( \ C_{2} \ \mathrm {[F]} \ \)を付加した回路を示す。この回路の周波数伝達関数を\( \ \displaystyle G(j\omega )=\frac {1+j\omega T_{3}}{1+j\omega T_{2}} \ \)で表したとき，\( \ T_{2} \ \mathrm {[s]} \ \)及び\( \ T_{3} \ \mathrm {[s]} \ \)を示す式として，正しいものを組み合わせたのは次のうちどれか。

\[
\begin{array}{cll}
\hline
(1) & 　T_{2}=C_{2}R　 & 　T_{3}=C_{1}R　 \\
\hline
(2) & 　T_{2}=C_{1}R　 & 　T_{3}=C_{2}R　 \\
\hline
(3) & 　T_{2}=\left( C_{1}+C_{2}\right) R　 & 　T_{3}=C_{2}R　 \\
\hline
(4) & 　\displaystyle T_{2}=\left( \frac {1}{C_{1}}+\frac {1}{C_{2}}\right) R　 & 　T_{3}=C_{2}R　 \\
\hline
(5) & 　T_{2}=C_{1}R　 & 　T_{3}=\left( C_{1}+C_{2}\right) R　 \\
\hline
\end{array}
\]

【ワンポイント解説】

抵抗とコンデンサを組み合わせた回路の周波数伝達関数を求める問題です。
自動制御の内容ですが，交流回路の合成インピーダンスや分圧の法則を前提知識として解いていく問題です。わからないという方は理論科目のテキスト等で復習しておくようにして下さい。

【解答】

(a)解答：(2)
入力電圧を\( \ V_{i} \ \mathrm {[V]} \ \)，出力電圧を\( \ V_{o} \ \mathrm {[V]} \ \)とすると，分圧の法則より，
\[
\begin{eqnarray}
V_{o} &=&\frac {\displaystyle \frac {1}{j\omega C_{1}}}{\displaystyle R+ \frac {1}{j\omega C_{1}}}V_{i} \\[ 5pt ] &=&\frac {\displaystyle \frac {1}{j\omega C_{1}}}{\displaystyle \frac {1+j\omega C_{1}R}{j\omega C_{1}}}V_{i} \\[ 5pt ] &=&\frac {1}{1+j\omega C_{1}R}V_{i} \\[ 5pt ] \frac {V_{o}}{V_{i}}&=&\frac {1}{1+j\omega C_{1}R} \\[ 5pt ] G(j\omega )&=&\frac {1}{1+j\omega C_{1}R} \\[ 5pt ] \end{eqnarray}
\] となり，\( \ \displaystyle G(j\omega )=\frac {1}{1+j\omega T_{1}} \ \)と係数比較すると，\( \ \displaystyle T_{1}=C_{1}R \ \)と求められる。

(b)解答：(3)
\( \ R \ \mathrm {[\Omega ]} \ \)と\( \ C_{2} \ \mathrm {[F]} \ \)の並列合成インピーダンス\( \ Z \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
Z &=&\frac {\displaystyle R\cdot \frac {1}{j\omega C_{2}}}{\displaystyle R+ \frac {1}{j\omega C_{2}}} \\[ 5pt ] &=&\frac {\displaystyle \frac {R}{j\omega C_{2}}}{\displaystyle \frac {1+j\omega C_{2}R}{j\omega C_{2}}} \\[ 5pt ] &=&\frac {R}{1+j\omega C_{2}R} \\[ 5pt ] \end{eqnarray}
\] であるから，入力電圧を\( \ V_{i} \ \mathrm {[V]} \ \)，出力電圧を\( \ V_{o} \ \mathrm {[V]} \ \)とすると，(a)の解答式を\( \ R→Z \ \)とすれば良いので，
\[
\begin{eqnarray}
G(j\omega )&=&\frac {1}{1+j\omega C_{1}Z} \\[ 5pt ] &=&\frac {1}{\displaystyle 1+j\omega C_{1}\cdot \frac {R}{1+j\omega C_{2}R}} \\[ 5pt ] &=&\frac {1}{\displaystyle 1+\frac {j\omega C_{1}R}{1+j\omega C_{2}R}} \\[ 5pt ] &=&\frac {1}{\displaystyle \frac {1+j\omega C_{2}R+j\omega C_{1}R}{1+j\omega C_{2}R}} \\[ 5pt ] &=&\frac {1+j\omega C_{2}R}{1+j\omega C_{1}R+j\omega C_{2}R} \\[ 5pt ] &=&\frac {1+j\omega C_{2}R}{1+j\omega \left( C_{1}+ C_{2}\right) R} \\[ 5pt ] \end{eqnarray}
\] となり，\( \ \displaystyle G(j\omega )=\frac {1+j\omega T_{3}}{1+j\omega T_{2}} \ \)と係数比較すると，\( \ T_{2}=\left( C_{1}+C_{2}\right) R \ \)及び\( \ T_{3}=C_{2}R \ \)と求められる。