《機械》〈直流機〉[H20:問1]直流機に発生する誘導起電力の原理に関する空欄穴埋問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

長さ\( \ l \ \mathrm {[m]} \ \)の導体を磁束密度\( \ B \ \mathrm {[T]} \ \)の磁束の方向と直角に置き，速度\( \ v \ \mathrm {[m / s]} \ \)で導体及び磁束に直角な方向に移動すると，導体にはフレミングの\( \ \fbox {　（ア）　} \ \)の法則により，\( \ e=\fbox {　（イ）　} \ \mathrm {[V]} \ \)の誘導起電力が発生する。

\( \ 1 \ \)極当たりの磁束が\( \ \mathit {\Phi } \ \mathrm {[Wb]} \ \)，磁極数が\( \ p \ \)，電機子総導体数が\( \ Z \ \)，巻線の並列回路数が\( \ a \ \)，電機子の直径が\( \ D \ \mathrm {[m]} \ \)なる直流機が速度\( \ n \ \mathrm {[{min }^{-1}]} \ \)で回転しているとき，周辺速度は\( \ \displaystyle v=πD \frac {n}{60} \ \mathrm {[m / s]} \ \)となり，直流機の正負のフラシ間には\( \ \fbox {　（ウ）　} \ \)本の導体が\( \ \fbox {　（エ）　} \ \)に接続されるので，電機子の誘導起電力\( \ E \ \)は，\( \ E=\fbox {　（オ）　} \ \mathrm {[V]} \ \)となる。

上記の記述中の空白箇所(ア)，(イ)，(ウ)，(エ)及び(オ)に当てはまる語句又は式として，正しいものを組み合わせたのは次のうちどれか。
\[
\begin{array}{cccc}
& （ア） & （イ） & （ウ） & （エ） & （オ） \\
\hline
(1) & 　右　手　 & 　Blv　 & 　\displaystyle \frac {Z}{a}　 & 　直　列　 & 　\displaystyle \frac {pZ}{60a}\mathit {\Phi }n　 \\
\hline
(2) & 　左　手　 & 　Blv　 & 　Za　 & 　直　列　 & 　\displaystyle \frac {pZa}{60}\mathit {\Phi }n　 \\
\hline
(3) & 　右　手　 & 　\displaystyle \frac {Bv}{l}　 & 　Za　 & 　並　列　 & 　\displaystyle \frac {pZa}{60}\mathit {\Phi }n　 \\
\hline
(4) & 　右　手　 & 　Blv　 & 　\displaystyle \frac {a}{Z}　 & 　並　列　 & 　\displaystyle \frac {pZ}{60a}\mathit {\Phi }n　 \\
\hline
(5) & 　左　手　 & 　\displaystyle \frac {Bv}{l}　 & 　\displaystyle \frac {Z}{a}　 & 　直　列　 & 　\displaystyle \frac {Z}{60pa}\mathit {\Phi }n　 \\
\hline
\end{array}
\]

【ワンポイント解説】

直流機の誘導起電力の発生原理に関する問題です。
今後後進の指導を予定されている方は原理を知っている必要があると思いますが，電験対策としては概要を理解し(オ)の空欄を公式として覚えておけば十分かと思います。

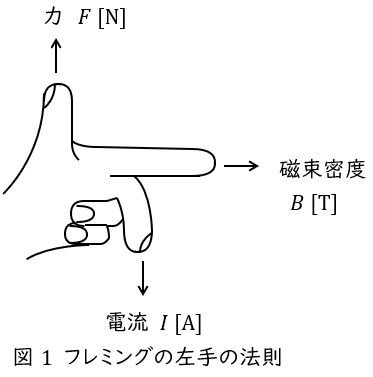
1.フレミングの左手の法則
中指を電流の向き，人差し指を磁界の向きに合わせると，親指の方向に力が働くという法則で，頭文字を取って「電磁力」と覚えます。
磁束密度の大きさ\( \ B \ \mathrm {[T]} \ \)，電流の大きさ\( \ I \ \mathrm {[A]} \ \)，直線状導体の長さを\( \ l \ \mathrm {[m]} \ \)とすると，導体に発生する電磁力\( \ F \ \mathrm {[N]} \ \)は，
\[
\begin{eqnarray}
F &=&BIl \\[ 5pt ] \end{eqnarray}
\] となります。

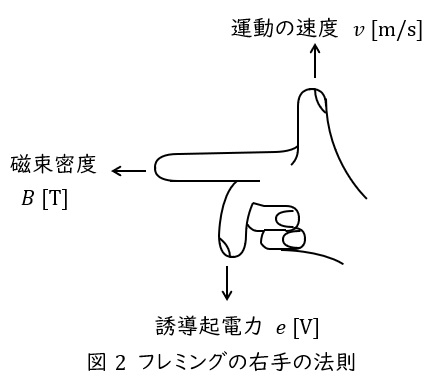
2.フレミングの右手の法則
親指を導体の運動方向（速度），人差し指を磁界（磁束密度）の方向にすると，中指の方向に誘導起電力が発生するという法則で，「電磁速」と覚えます。
磁束密度の大きさを\( \ B \ \mathrm {[T]} \ \)，導体の速度を\( \ v \ \mathrm {[m／s]} \ \)，導体の長さを\( \ l \ \mathrm {[m]} \ \)とすると，誘導起電力の大きさ\( \ e \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
e &=& Blv \\[ 5pt ] \end{eqnarray}
\] となります。

3.直流機の誘導起電力の発生原理
直流機は回転子と固定子から構成され，内側が回転子，外側が固定子となっています。
基本は回転電機子形（例外もあります）で，電機子は電機子鉄心のスロットに電機子巻線が巻かれた構造をしています。
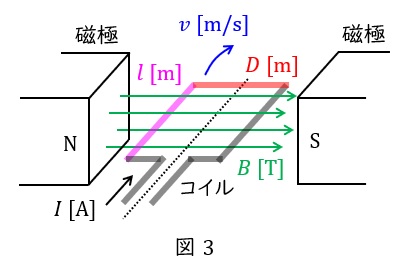
模式図として図3のように，磁束密度\( \ B \ \mathrm {[T]} \ \)の中に，辺の長さが\( \ l \ \mathrm {[m]} \ \)のコイルを速度\( \ v \ \mathrm {[m / s]} \ \)で回転させた例を考えると，コイルの辺に発生する誘導起電力\( \ e \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
e &=& Blv \\[ 5pt ] \end{eqnarray}
\] となります。仮に磁極数が\( \ p \ \)，\( \ 1 \ \)極あたりの磁束が\( \ \phi \ \mathrm {[Wb]} \ \)であるとすると，磁束密度\( \ B \ \mathrm {[T]} \ \)は，
\[
\begin{eqnarray}
B &=& \frac {p\phi}{S} \\[ 5pt ] &=& \frac {p\phi}{\pi Dl} \\[ 5pt ] \end{eqnarray}
\] となり，さらに，回転速度が\( \ N \ \mathrm {[{min}^{-1}]} \ \)であるとすれば，
\[
\begin{eqnarray}
v &=& \pi D \cdot \frac {N}{60} \\[ 5pt ] &=& \frac {\pi D N}{60} \\[ 5pt ] \end{eqnarray}
\] となるので，誘導起電力は，
\[
\begin{eqnarray}
e &=& Blv \\[ 5pt ] &=& \frac {p\phi}{\pi Dl}\cdot l\cdot \frac {\pi D N}{60} \\[ 5pt ] &=& \frac {p\phi N}{60} \\[ 5pt ] \end{eqnarray}
\] となります。

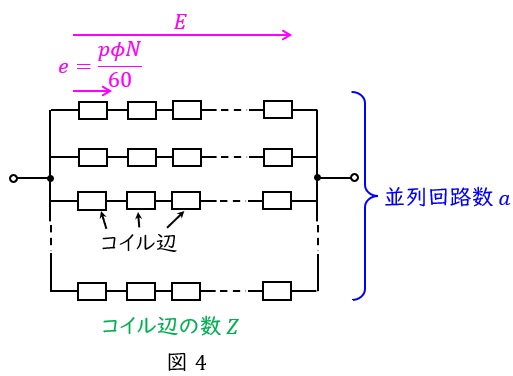
直流機は，図4に示すようにコイル（導体）が直並列された構造であるため，全体の誘導起電力\( \ E \ \mathrm {[V]} \ \)は，全コイル数（導体数）を\( \ Z \ \)，並列回路数を\( \ a \ \)とすると，直列接続数が\( \ \displaystyle \frac {Z}{a} \ \)となるため，
\[
\begin{eqnarray}
E &=& e\cdot \frac {Z}{a} \\[ 5pt ] &=& \frac {p\phi N}{60}\cdot \frac {Z}{a} \\[ 5pt ] &=& \frac {pZ}{60a}\phi N \\[ 5pt ] \end{eqnarray}
\] と求められます。この式は公式として覚えておきましょう。