Contents
【問題】
【難易度】★★☆☆☆(やや易しい)
近年,広く普及してきたヒートポンプは,外部から機械的な仕事\( \ W \ \mathrm {[J]} \ \)を与え,\( \ \fbox { (ア) } \ \)熱源より熱量\( \ Q_{1} \ \mathrm {[J]} \ \)を吸収して,\( \ \fbox { (イ) } \ \)部へ熱量\( \ Q_{2} \ \mathrm {[J]} \ \)を放出する機関のことである。この場合(定常状態では),熱量\( \ Q_{1} \ \mathrm {[J]} \ \)と熱量\( \ Q_{2} \ \mathrm {[J]} \ \)の間には\( \ \fbox { (ウ) } \ \)の関係が成り立ち,ヒートポンプの効率\( \ \eta \ \)は,加熱サイクルの場合\( \ \fbox { (エ) } \ \)となり\( \ 1 \ \)より大きくなる。この効率\( \ \eta \ \)は\( \ \fbox { (オ) } \ \)係数\( \ \left( \mathrm {COP} \right) \ \)と呼ばれている。
上記の記述中の空白箇所(ア),(イ),(ウ),(エ)及び(オ)に当てはまる語句又は式として,正しいものを組み合わせたのは次のうちどれか。
\[
\begin{array}{cccccc}
& (ア) & (イ) & (ウ) & (エ) & (オ) \\
\hline
(1) & 低 温 & 高 温 & Q_{2}=Q_{1}+W & \displaystyle \frac {Q_{2}}{W} & 成 績 \\
\hline
(2) & 高 温 & 低 温 & Q_{2}=Q_{1}+W & \displaystyle \frac {Q_{1}}{W} & 評 価 \\
\hline
(3) & 低 温 & 高 温 & Q_{2}=Q_{1}+W & \displaystyle \frac {Q_{1}}{W} & 成 績 \\
\hline
(4) & 高 温 & 低 温 & Q_{2}=Q_{1}-W & \displaystyle \frac {Q_{2}}{W} & 成 績 \\
\hline
(5) & 低 温 & 高 温 & Q_{2}=Q_{1}-W & \displaystyle \frac {Q_{2}}{W} & 評 価 \\
\hline
\end{array}
\]
【ワンポイント解説】
ヒートポンプの原理に関する問題です。
ヒートポンプの図は描けなくても良いですが,機械的仕事と熱量の関係は十分に理解しておくようにして下さい。また,本問では出題されていませんが,計算問題も多く出題される内容ですので,合わせて学習しておくようにしましょう。
1.ヒートポンプの構成機器
ヒートポンプは,外部から機械的な仕事を与え,低温熱源から熱を吸収して,高温部へ熱を放出し,機械的仕事以上の熱エネルギーを生み出すことができる機関で,エアコンや給湯器等に使用されています。
ヒートポンプのフローを図1に示します。冷房時が青線,暖房時は赤線の流れとなります。冷房時を例に示します。
蒸発器:膨張弁からの低温低圧の液を蒸発させ気化させます。
四方弁:暖房冷房時に圧縮機に流れる媒体の向きを同じにするために向きを変えるものです。
圧縮機:蒸発器から出た低圧の蒸気を高圧蒸気にします。
凝縮器:圧縮機で高温高圧となった蒸気を凝縮し,液化させます。
膨張弁:凝縮器から出た液を膨張し,低温低圧の液にします。
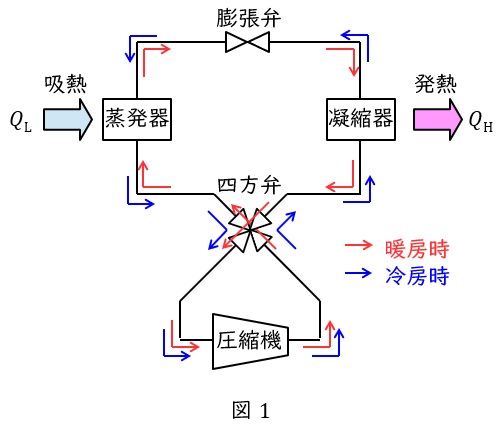
※図1において,暖房時には熱交換器である蒸発器と凝縮器の役割が逆となります。
2.ヒートポンプの成績係数(\( \ \mathrm {COP} \ \))
図1において,蒸発器の吸熱量\( \ Q_{\mathrm {L}} \ \)及び圧縮機にかける仕事量\( \ W \ \)と凝縮器の放熱量\( \ Q_{\mathrm {H}} \ \)は等しいので,
\[
\begin{eqnarray}
Q_{\mathrm {H}}&=&Q_{\mathrm {L}}+W \\[ 5pt ]
\end{eqnarray}
\]
という関係があり,冷房時と暖房時の成績係数\( \ \mathrm {{COP}_{L}} \ \),\( \ \mathrm {{COP}_{H}} \ \)は,
\[
\begin{eqnarray}
\mathrm {{COP}_{L}}&=&\frac {Q_{\mathrm {L}}}{W} \\[ 5pt ]
\mathrm {{COP}_{H}}&=&\frac {Q_{\mathrm {H}}}{W} \\[ 5pt ]
&=&\frac {Q_{\mathrm {L}}+W}{W} \\[ 5pt ]
&=&1+\frac {Q_{\mathrm {L}}}{W} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
解答:(1)
(ア)
ワンポイント解説「1.ヒートポンプの構成機器」の通り,ヒートポンプは低温熱源から熱量を吸収します。
(イ)
ワンポイント解説「1.ヒートポンプの構成機器」の通り,ヒートポンプは高温部へ熱量を放出します。
(ウ)
ワンポイント解説「2.ヒートポンプの成績係数(\( \ \mathrm {COP} \ \))」の通り,機械的な仕事\( \ W \ \mathrm {[J]} \ \),吸収熱量\( \ Q_{1} \ \mathrm {[J]} \ \),放出熱量\( \ Q_{2} \ \mathrm {[J]} \ \)の間には,\( \ Q_{2}=Q_{1}+W \ \)の関係があります。
(エ)
ワンポイント解説「2.ヒートポンプの成績係数(\( \ \mathrm {COP} \ \))」の通り,加熱サイクルにおいてヒートポンプの効率は\( \ \displaystyle \frac {Q_{2}}{W} \ \)となります。
(オ)
ワンポイント解説「2.ヒートポンプの成績係数(\( \ \mathrm {COP} \ \))」の通り,ヒートポンプの効率は成績係数と呼ばれます。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは