Contents
【問題】
【難易度】★★★☆☆(普通)
図1は,\( \ \mathrm {IGBT} \ \)を用いた単相ブリッジ接続の電圧形インバータを示す。直流電圧\( \ E_{d} \ \mathrm {[V]} \ \)は,一定値と見なせる。出力端子には,インダクタンス\( \ L \ \mathrm {[H]} \ \)で抵抗値\( \ R \ \mathrm {[\Omega ]} \ \)の誘導性負荷が接続されている。
図2は,このインバータの動作波形である。時刻\( \ t=0 \ \mathrm {[s]} \ \)で\( \ \mathrm {IGBT \ Q_{3}} \ \)及び\( \ \mathrm {Q_{4}} \ \)のゲート信号をオフにするとともに\( \ \mathrm {Q_{1}} \ \)及び\( \ \mathrm {Q_{2}} \ \)のゲート信号をオンにすると,出力電圧\( \ v_{a} \ \mathrm {[V]} \ \)は\( \ E_{d} \ \mathrm {[V]} \ \)となる。\( \ \displaystyle t=\frac {T}{2} \ \mathrm {[s]} \ \)で\( \ \mathrm {Q_{1}} \ \)及び\( \ \mathrm {Q_{2}} \ \)のゲート信号をオフにするとともに\( \ \mathrm {Q_{3}} \ \)及び\( \ \mathrm {Q_{4}} \ \)のゲート信号をオンにすると,\( \ v_{a} \ \mathrm {[V]} \ \)は\( \ -E_{d} \ \mathrm {[V]} \ \)となる。これを周期\( \ T \ \mathrm {[s]} \ \)で繰り返して方形波電圧を出力する。
出力電流\( \ i_{a} \ \mathrm {[A]} \ \)は,\( \ t=0 \ \mathrm {[s]} \ \)で\( \ -I_{p} \ \mathrm {[A]} \ \)になっているものとする。負荷の時定数は\( \ \displaystyle \tau =\frac {L}{R} \ \mathrm {[s]} \ \)である。\( \ \displaystyle t=0~\frac {T}{2} \ \mathrm {[s]} \ \)では,時間の関数\( \ i_{a} \left( t \right) \ \)は次式となる。
\[
\begin{eqnarray}
i_{a} \left( t \right) &=&-I_{p}\mathrm {e}^{-\frac {t}{\tau }}+\frac {E_{d}}{R}\left( 1-\mathrm {e}^{-\frac {t}{\tau }}\right) \\[ 5pt ]
\end{eqnarray}
\]
定常的に動作しているときには,周期条件から\( \ \displaystyle t=\frac {T}{2} \ \mathrm {[s]} \ \)で出力電流は\( \ I_{p} \ \mathrm {[A]} \ \)となり,次式が成り立つ。
\[
\begin{eqnarray}
i_{a} \left( \frac {T}{2} \right) &=&-I_{p}\mathrm {e}^{-\frac {T}{2\tau }}+\frac {E_{d}}{R}\left( 1-\mathrm {e}^{-\frac {T}{2\tau }}\right) =I_{p} \\[ 5pt ]
\end{eqnarray}
\]
このとき,次の(a)及び(b)に答えよ。
ただし,バルブデバイス(\( \ \mathrm {IGBT} \ \)及びダイオード)での電圧降下は無視するものとする。
(a) 時刻\( \ \displaystyle t=\frac {T}{2} \ \mathrm {[s]} \ \)の直前では\( \ \mathrm {Q_{1}} \ \)及び\( \ \mathrm {Q_{2}} \ \)がオンしており,出力電流は直流電源から\( \ \mathrm {Q_{1}} \ \)→負荷→\( \ \mathrm {Q_{2}} \ \)の経路で流れている。\( \ \displaystyle t=\frac {T}{2} \ \mathrm {[s]} \ \)で\( \ \mathrm {IGBT \ Q_{1}} \ \)及び\( \ \mathrm {Q_{2}} \ \)のゲート信号をオフにするとともに\( \ \mathrm {Q_{3}} \ \)及び\( \ \mathrm {Q_{4}} \ \)のゲート信号をオンにした。その直後(図2で,\( \ \displaystyle t=\frac {T}{2} \ \mathrm {[s]} \ \)から,出力電流が\( \ 0 \ \mathrm {[A]} \ \)になる\( \ t=t_{r} \ \mathrm {[s]} \ \)までの期間),出力電流が流れるバルブデバイスとして,正しいものを組み合わせたのは次のうちどれか。
(1) \( \ \mathrm {Q_{1}},\mathrm {Q_{2}} \ \) (2) \( \ \mathrm {Q_{3}},\mathrm {Q_{4}} \ \) (3) \( \ \mathrm {D_{1}},\mathrm {D_{2}} \ \)
(4) \( \ \mathrm {D_{3}},\mathrm {D_{4}} \ \) (5) \( \ \mathrm {Q_{3}},\mathrm {Q_{4}},\mathrm {D_{1}},\mathrm {D_{2}} \ \)
(b) \( \ E_{d}=200 \ \mathrm {[V]} \ \),\( \ L=10 \ \mathrm {[mH]} \ \),\( \ R=2.0 \ \mathrm {[\Omega ]} \ \),\( \ T=10 \ \mathrm {[ms]} \ \)としたとき,\( \ I_{p} \ \mathrm {[A]} \ \)の値として,最も近いのは次のうちどれか。ただし,\( \ \mathrm {e}=2.718 \ \)とする。
(1) \( \ 32 \ \) (2) \( \ 46 \ \) (3) \( \ 63 \ \) (4) \( \ 76 \ \) (5) \( \ 92 \ \)
【ワンポイント解説】
単相ブリッジ電圧形インバータの動作と電流波高値を導出する問題です。
問題文が長く一見難しそうに見える問題ですが,(a)は動作のメカニズムを知っていれば即座に解ける問題,(b)も数値計算の数学の問題です。
令和4年上期問16にも類題が出題されていますので,一緒に学習しておくようにして下さい。
1.単相ブリッジインバータの動作
本問の単相ブリッジインバータの動作は以下の通りとなります。各素子の役割や電流の流れを理解していると様々な問題に対応できることになります。
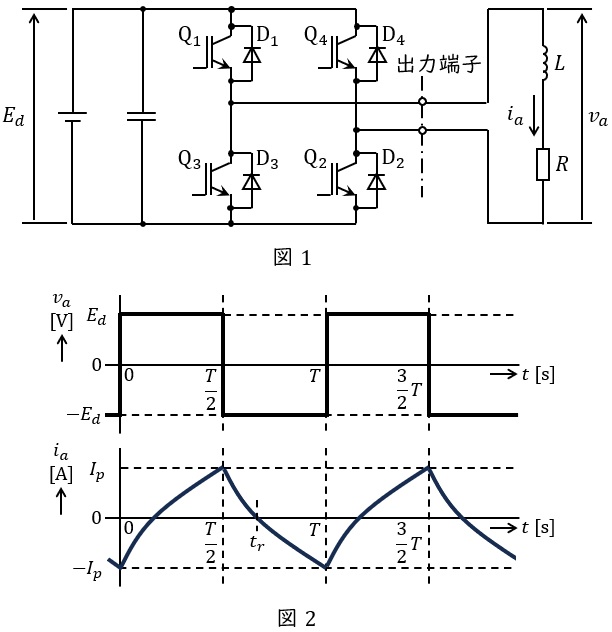
①\( \ \mathrm {Q_{1}} \ \)及び\( \ \mathrm {Q_{2}} \ \)が\( \ \mathrm {ON} \ \)になり十分に時間が経過した後
図1-1に示すように\( \ E_{d} \ \)→\( \ \mathrm {Q_{1}} \ \)→\( \ L \ \)→\( \ R \ \)→\( \ \mathrm {Q_{2}} \ \)→\( \ E_{d} \ \)と導通します。
図1-1より出力端子の電圧は\( \ v_{a}=E_{d} \ \)となり,\( \ i_{a}>0 \ \)でリアクトル\( \ L \ \)にエネルギーが蓄えられます。
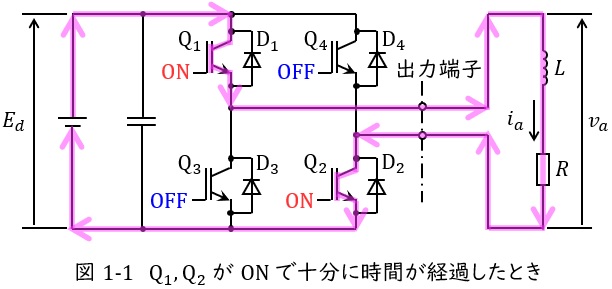
②\( \ \mathrm {Q_{3}} \ \)及び\( \ \mathrm {Q_{4}} \ \)が\( \ \mathrm {ON} \ \)になった直後
リアクトル\( \ L \ \)が電流\( \ i_{a}>0 \ \)を維持しようとするので,リアクトル\( \ L \ \)に蓄えられているエネルギーが放出し,図1-2に示すように\( \ L \ \)→\( \ R \ \)→\( \ \mathrm {D_{4}} \ \)→\( \ E_{d} \ \)→\( \ \mathrm {D_{3}} \ \)→\( \ L \ \)と導通します。
図1-2より出力端子の電圧は\( \ v_{a}=-E_{d} \ \)となり,\( \ i_{a}>0 \ \)でリアクトル\( \ L \ \)のエネルギーが放出されます。
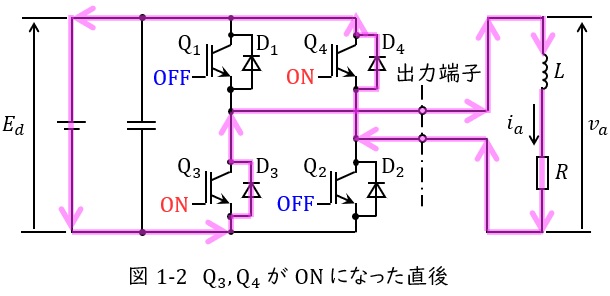
③\( \ \mathrm {Q_{3}} \ \)及び\( \ \mathrm {Q_{4}} \ \)が\( \ \mathrm {ON} \ \)になり十分に時間が経過した後
リアクトル\( \ L \ \)のエネルギーがなくなり,図1-3に示すように\( \ E_{d} \ \)→\( \ \mathrm {Q_{4}} \ \)→\( \ R \ \)→\( \ L \ \)→\( \ \mathrm {Q_{3}} \ \)→\( \ E_{d} \ \)と導通します。
図1-3より出力端子の電圧は\( \ v_{a}=-E_{d} \ \)となり,\( \ i_{a}<0 \ \)でリアクトル\( \ L \ \)にエネルギーが蓄えられます。
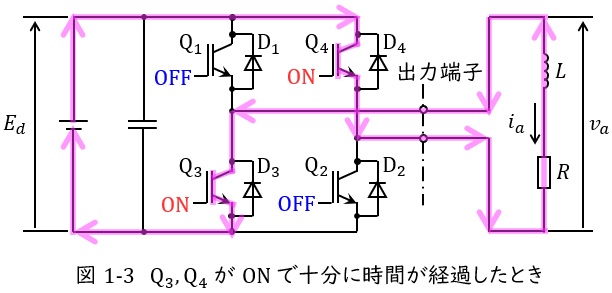
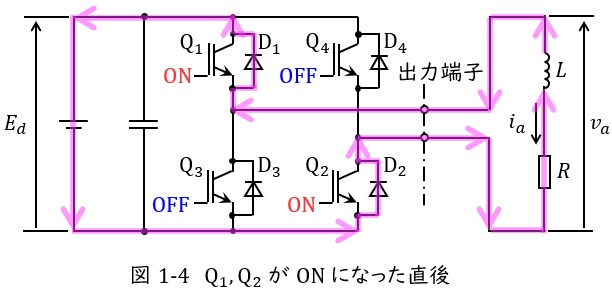
④\( \ \mathrm {Q_{1}} \ \)及び\( \ \mathrm {Q_{2}} \ \)が\( \ \mathrm {ON} \ \)になった直後
リアクトル\( \ L \ \)が電流\( \ i_{a}<0 \ \)を維持しようとするので,リアクトル\( \ L \ \)に蓄えられているエネルギーが放出し,図1-4に示すように\( \ L \ \)→\( \ \mathrm {D_{1}} \ \)→\( \ E_{d} \ \)→\( \ \mathrm {D_{2}} \ \)→\( \ R \ \)→\( \ L \ \)と導通します。
図1-4より出力端子の電圧は\( \ v_{a}=E_{d} \ \)となり,\( \ i_{a}<0 \ \)でリアクトル\( \ L \ \)のエネルギーが放出されます。
以降①~④を繰り返します。
【解答】
(a)解答:(4)
ワンポイント解説「1.単相ブリッジインバータの動作」の通り,\( \ \displaystyle t=\frac {T}{2} \ \mathrm {[s]} \ \)から,出力電流が\( \ 0 \ \mathrm {A} \ \)になる\( \ t=t_{r} \ \mathrm {[s]} \ \)までの期間は,\( \ v_{a}=-E_{d} \ \)で\( \ i_{a}>0 \ \)の状態であるから,図1-2の状態である。
したがって,導通しているのは\( \ \mathrm {D_{3}} , \mathrm {D_{4}} \ \)と求められる。
(b)解答:(2)
問題文の\( \ \displaystyle t=\frac {T}{2} \ \mathrm {[s]} \ \)で出力電流は\( \ I_{p} \ \mathrm {[A]} \ \)となる式に各値を代入して整理すると,
\[
\begin{eqnarray}
I_{p}&=&-I_{p}\mathrm {e}^{-\frac {T}{2\tau }}+\frac {E_{d}}{R}\left( 1-\mathrm {e}^{-\frac {T}{2\tau }}\right) \\[ 5pt ]
&=&-I_{p}\mathrm {e}^{-\frac {RT}{2L}}+\frac {E_{d}}{R}\left( 1-\mathrm {e}^{-\frac {RT}{2L}}\right) \\[ 5pt ]
&=&-I_{p}\times \mathrm {2.718}^{-\frac {2.0\times 10\times 10^{-3}}{2\times 10\times 10^{-3}}}+\frac {200}{2.0}\times \left( 1-\mathrm {2.718}^{-\frac {2.0\times 10\times 10^{-3}}{2\times 10\times 10^{-3}}}\right) \\[ 5pt ]
&=&-I_{p}\times \mathrm {2.718}^{-1}+100\times \left( 1-\mathrm {2.718}^{-1}\right) \\[ 5pt ]
&=&-\frac {I_{p}}{2.718}+100\times \left( 1-\frac {1}{2.718}\right) \\[ 5pt ]
\left(1+\frac {1}{2.718} \right) I_{p}&=&100\times \left( 1-\frac {1}{2.718}\right) \\[ 5pt ]
1.368I_{p}&≒&63.21 \\[ 5pt ]
I_{p}&≒&46 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは