Contents
【問題】
【難易度】★★★★☆(やや難しい)
\( \ \mathrm {JK-FF} \ \)(\( \ \mathrm {JK-} \ \)フリップフロップ)の動作とそれを用いた回路について,次の(a)及び(b)に答えよ。
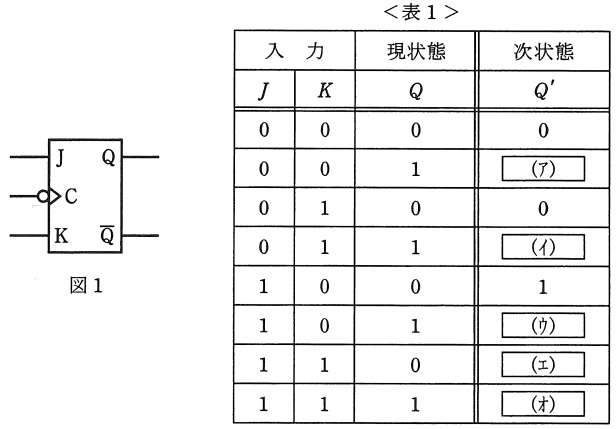
(a) 図1の\( \ \mathrm {JK-FF} \ \)の状態遷移について考える。\( \ \mathrm {JK-FF} \ \)の\( \ J \ \),\( \ K \ \)の入力時における出力を\( \ Q \ \)(現状態),\( \ J \ \),\( \ K \ \)の入力とクロックパルスの立下がりによって変化する\( \ Q \ \)の変化後の状態(次状態)の出力を\( \ Q^{\prime } \ \)として,その状態遷移を表1のようにまとめる。表1中の空白箇所(ア),(イ),(ウ),(エ)及び(オ)に当てはまる真理値として,正しいものを組み合わせたのは次のうちどれか。
\[
\begin{array}{cccccc}
& (ア) & (イ) & (ウ) & (エ) & (オ) \\
\hline
(1) & 0 & 0 & 0 & 1 & 1 \\
\hline
(2) & 0 & 1 & 0 & 0 & 0 \\
\hline
(3) & 1 & 1 & 0 & 1 & 1 \\
\hline
(4) & 1 & 0 & 1 & 1 & 0 \\
\hline
(5) & 1 & 0 & 1 & 0 & 1 \\
\hline
\end{array}
\]
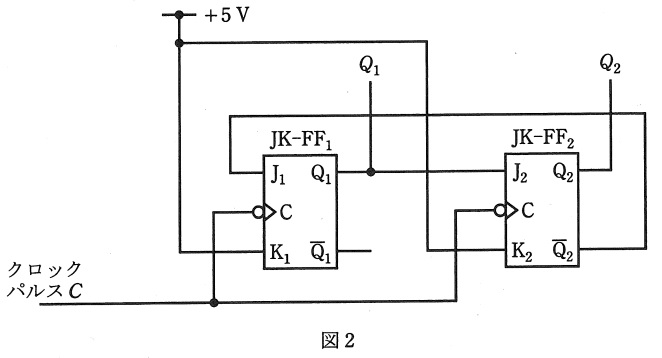
(b) \( \ 2 \ \)個の\( \ \mathrm {JK-FF} \ \)を用いた図2の回路を考える。この回路において,\( \ +5 \ \mathrm {[V]} \ \)を\( \ “1” \ \),\( \ 0 \ \mathrm {[V]} \ \)を\( \ “0” \ \)と考えたとき,クロックパルス\( \ C \ \)に対する回路の出力\( \ Q_{1} \ \)及び\( \ Q_{2} \ \)のタイムチャートとして,正しいのは次のうちどれか。
【ワンポイント解説】
保持回路の一つである\( \ \mathrm {JK-FF} \ \)に関する出題です。
数年に\( \ 1 \ \)回程度出題されるフリップフロップですが,難易度が高めであること,出題が選択問題であること等を考えると捨て問としてしまっても良いかもしれません。
1.フリップフロップ
論理回路のうち出力を一時的に保持することができる記憶回路のことをいいます。
大学の電子工学では,細かな回路構成も勉強しますが,電験においてはその概要と真理値表を見ておけば十分かと思います。
①\( \ \mathrm {RS} \ \)フリップフロップ
図3に示すような回路構成で,フリップフロップとしては最も単純な回路となります。真理値表は表1のようになります。
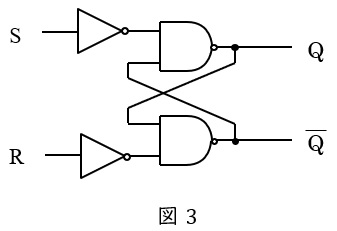
表 1
\[
\begin{array}{|c|c|c|c|}
\hline
\mathrm {S} & \mathrm {R} & \mathrm {Q} & \overline {\mathrm {Q}} \\
\hline
0 & 0 & 保持 & 保持 \\
0 & 1 & 0 & 1 \\
1 & 0 & 1 & 0 \\
1 & 1 & 禁止 & 禁止 \\
\hline
\end{array}
\]
②\( \ \mathrm {JK} \ \)フリップフロップ
回路は\( \ \mathrm {RS} \ \)フリップフロップに\( \ \mathrm {AND} \ \)回路を接続したような回路ですが,真理値表は表2のように\( \ \mathrm {RS} \ \)フリップフロップをベースとして,入力を共に\( \ 1 \ \)とした場合に出力が反転するフリップフロップとなります。
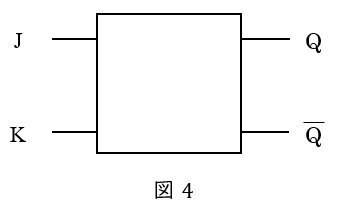
表 2
\[
\begin{array}{|c|c|c|c|}
\hline
\mathrm {J} & \mathrm {K} & \mathrm {Q} & \overline {\mathrm {Q}} \\
\hline
0 & 0 & 保持 & 保持 \\
0 & 1 & 0 & 1 \\
1 & 0 & 1 & 0 \\
1 & 1 & 反転 & 反転 \\
\hline
\end{array}
\]
③\( \ \mathrm {T} \ \)フリップフロップ
入力\( \ \mathrm {T} \ \)が\( \ 0 \ \)のとき出力を保持し,\( \ 1 \ \)のとき出力を反転するフリップフロップで,真理値表は表3のようになります。\( \ 0→1 \ \)の立ち上がり時や\( \ 1→0 \ \)の立ち下がり時のトリガにより動作するものもあります。
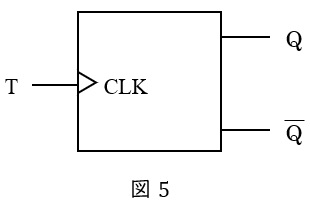
表 3
\[
\begin{array}{|c|c|c|}
\hline
\mathrm {T} & \mathrm {Q} & \overline {\mathrm {Q}} \\
\hline
0 & 保持 & 保持 \\
1 & 反転 & 反転 \\
\hline
\end{array}
\]
④\( \ \mathrm {D} \ \)フリップフロップ
入力が\( \ \mathrm {CLK} \ \)と\( \ \mathrm {D} \ \)があり,\( \ \mathrm {CLK} \ \)が\( \ 0 \ \)のとき出力を保持し,\( \ \mathrm {CLK} \ \)が\( \ 1 \ \)のとき\( \ \mathrm {D} \ \)を\( \ \mathrm {Q} \ \)に出力するフリップフロップで真理値表は表4のようになります。\( \ 0→1 \ \)の立ち上がり時や\( \ 1→0 \ \)の立ち下がり時のトリガにより動作するものもあります。
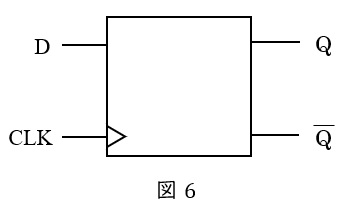
表 4
\[
\begin{array}{|c|c|c|c|}
\hline
\mathrm {CLK} & \mathrm {D} & \mathrm {Q} & \overline {\mathrm {Q}} \\
\hline
0 & 0 & 保持 & 保持 \\
0 & 1 & 保持 & 保持 \\
1 & 0 & 0 & 1 \\
1 & 1 & 1 & 0 \\
\hline
\end{array}
\]
【解答】
(a)解答:(4)
ワンポイント解説「1.フリップフロップ」の表2の通りです。
(ア)
入力\( \ J \ \)及び\( \ K \ \)がともに\( \ 0 \ \)なので,\( \ Q \ \)は保持され\( \ 1 \ \)が出力されます。
(イ)
入力\( \ J \ \)が\( \ 0 \ \),入力\( \ K \ \)が\( \ 1 \ \)なので,\( \ Q \ \)は\( \ 0 \ \)が出力されます。
(ウ)
入力\( \ J \ \)が\( \ 1 \ \),入力\( \ K \ \)が\( \ 0 \ \)なので,\( \ Q \ \)は\( \ 1 \ \)が出力されます。
(エ)
入力\( \ J \ \)及び\( \ K \ \)がともに\( \ 1 \ \)なので,\( \ Q \ \)は反転され\( \ 1 \ \)が出力されます。
(オ)
入力\( \ J \ \)及び\( \ K \ \)がともに\( \ 1 \ \)なので,\( \ Q \ \)は反転され\( \ 0 \ \)が出力されます。
(b)解答:(5)
入力\( \ \mathrm {K_{1}} \ \)及び\( \ \mathrm {K_{2}} \ \)には\( \ +5 \ \mathrm {[V]} \ \)が接続されているので,入力はともに\( \ 1 \ \)であり,タイムチャートに合わせ\( \ Q_{1} \ \)及び\( \ Q_{2} \ \)の初期値は\( \ 0 \ \)とすると,初期状態は図2-1のようになります。
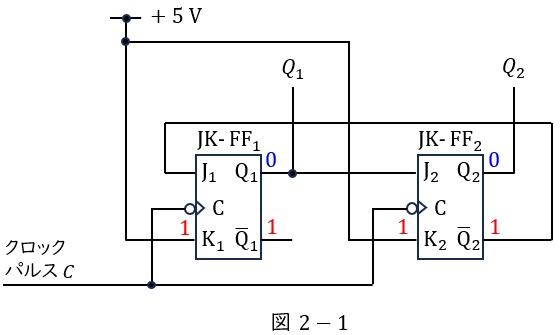
この状態で,クロックパルス\( \ C \ \)の立ち下がりがあると,\( \ \mathrm {J_{1}} \ \)には\( \ \mathrm {\overline {Q}_{2}} \ \)の\( \ 1 \ \),\( \ \mathrm {J_{2}} \ \)には\( \ \mathrm {Q_{1}} \ \)の\( \ 0 \ \)が入力されている状態なので,\( \ \mathrm {Q_{1}} \ \)は反転して\( \ 1 \ \),\( \ \mathrm {Q_{2}} \ \)は\( \ 0 \ \)が出力され,図2-2のようになります。
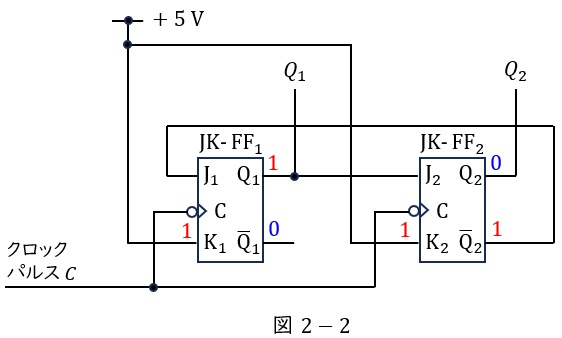
図2-2の状態で,クロックパルス\( \ C \ \)の立ち下がりがあると,\( \ \mathrm {J_{1}} \ \)には\( \ \mathrm {\overline {Q}_{2}} \ \)の\( \ 1 \ \),\( \ \mathrm {J_{2}} \ \)には\( \ \mathrm {Q_{1}} \ \)の\( \ 1 \ \)が入力されている状態なので,\( \ \mathrm {Q_{1}} \ \)は反転して\( \ 0 \ \),\( \ \mathrm {Q_{2}} \ \)も反転して\( \ 1 \ \)が出力され,図2-3のようになります。
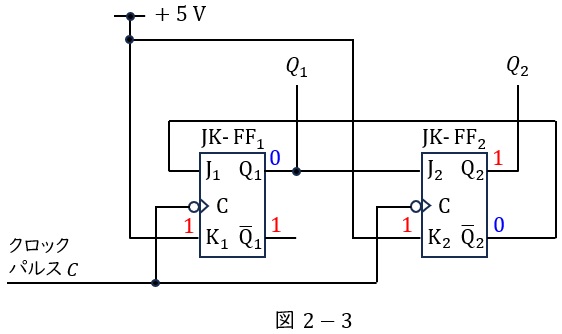
図2-3の状態で,クロックパルス\( \ C \ \)の立ち下がりがあると,\( \ \mathrm {J_{1}} \ \)には\( \ \mathrm {\overline {Q}_{2}} \ \)の\( \ 0 \ \),\( \ \mathrm {J_{2}} \ \)には\( \ \mathrm {Q_{1}} \ \)の\( \ 0 \ \)が入力されている状態なので,\( \ \mathrm {Q_{1}} \ \)は\( \ 0 \ \),\( \ \mathrm {Q_{2}} \ \)も\( \ 0 \ \)が出力され,図2-4のようになります。
図2-4は初期状態である図2-1と同じ状態なので,以後繰り返すことになります。
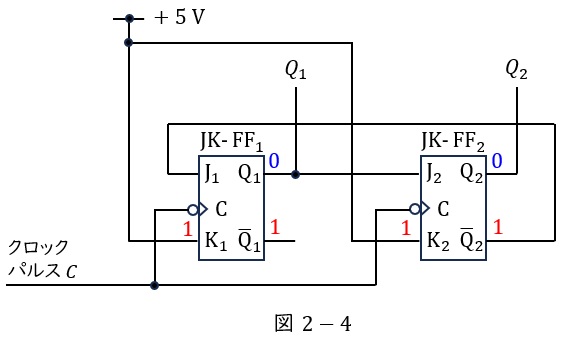
以上の内容と一致しているタイムチャートは(5)となります。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは