《機械》〈変圧器〉[H22:問8]接地変圧器の二次抵抗の一次換算値に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

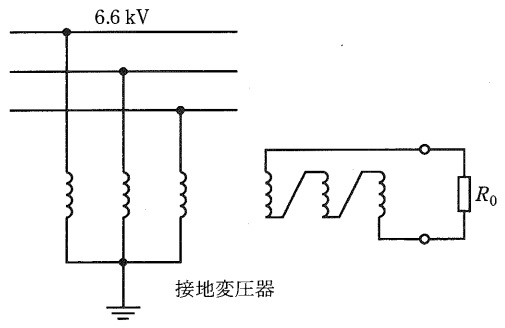
単相変圧器\( \ 3 \ \)台が図に示すように\( \ 6.6 \ \mathrm {[kV]} \ \)電路に接続されている。一次側は星形\( \ \left( \mathrm {Y} \right) \ \)結線，二次側は開放三角結線とし，一次側中性点は大地に接続され，二次側開放端子には図のように抵抗\( \ R_{0} \ \)が負荷として接続されている。三相電圧が平衡している通常の状態では，各相が打ち消しあうため二次側開放端子には電圧は現れないが，電路のバランスが崩れ不平衡になった場合や電路に地絡事故などが発生した場合には，二次側開放端子に電圧が現れる。このとき，二次側の抵抗負荷\( \ R_{0} \ \)は各相が均等に負担することになる。

いま，各単相変圧器の定格一次電圧が\( \ \displaystyle \frac {6.6}{\sqrt {3}} \ \mathrm {[kV]} \ \)，定格二次電圧が\( \ \displaystyle \frac {110}{\sqrt {3}} \ \mathrm {[V]} \ \)で，二次接続抵抗\( \ R_{0}=10 \ \mathrm {[\Omega ]} \ \)の場合，一次側に換算した\( \ 1 \ \)相当たりの二次抵抗\( \ \mathrm {[k\Omega ]} \ \)の値として，最も近いのは次のうちどれか。

ただし，変圧器は理想変圧器であり，一次巻線，二次巻線の抵抗及び損失は無視するものとする。

　(1)　\( \ 4.00 \ \)　　(2)　\( \ 6.93 \ \)　　(3)　\( \ 12.0 \ \)　　(4)　\( \ 20.8 \ \)　　(5)　\( \ 36.0 \ \)　

【ワンポイント解説】

接地変圧器の抵抗値の一次側換算に関する問題です。
接地変圧器の問題はあまり多くありませんが，二次側の抵抗値\( \ R_{0} \ \)は問題文にもあるように各相が均等に負担する，すなわち\( \ 1 \ \)相当たり\( \ \displaystyle \frac {R_{0}}{3} \ \)ずつ分担することは，問題文に与えられていなくても答えられるようにしておきましょう。

1.変圧器の巻数比と変圧比，変流比の関係
変圧器の一次側の巻数\( \ N_{1} \ \)，電圧\( \ V_{1} \ \mathrm {[V]} \ \)，電流\( \ I_{1} \ \mathrm {[A]} \ \)，二次側の巻数\( \ N_{2} \ \)，電圧\( \ V_{2} \ \mathrm {[V]} \ \)，電流\( \ I_{2} \ \mathrm {[A]} \ \)とすると，巻数比\( \ \displaystyle a=\frac {N_{1}}{N_{2}} \ \)は，
\[
\begin{eqnarray}
a&=&\frac {N_{1}}{N_{2}} =\frac {V_{1}}{V_{2}}=\frac {I_{2}}{I_{1}} \\[ 5pt ] \end{eqnarray}
\] となります。インピーダンスは電圧を電流で割ったものであるため，一次側換算のインピーダンス\( \ Z_{1} \ \mathrm {[\Omega ]} \ \)，二次側換算のインピーダンス\( \ Z_{2} \ \mathrm {[\Omega ]} \ \)とすると，
\[
\begin{eqnarray}
\frac {Z_{1}}{Z_{2}} &=&\frac {\displaystyle \frac {V_{1}}{I_{1}}}{\displaystyle \frac {V_{2}}{I_{2}}} \\[ 5pt ] &=&\frac {V_{1}}{I_{1}}\times \frac {I_{2}}{V_{2}} \\[ 5pt ] &=&\frac {V_{1}}{V_{2}}\times \frac {I_{2}}{I_{1}} \\[ 5pt ] &=&\left( \frac {N_{1}}{N_{2}} \right) ^{2} \\[ 5pt ] &=&a^{2} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(3)
接地変圧器の巻数比\( \ a \ \)は，ワンポイント解説「1.変圧器の巻数比と変圧比，変流比の関係」の通り，
\[
\begin{eqnarray}
a&=&\frac {V_{1}}{V_{2}} \\[ 5pt ] &=&\frac {\displaystyle \frac {6.6\times 10^{3}}{\sqrt {3}}}{\displaystyle \frac {110}{\sqrt {3}}} \\[ 5pt ] &=&60 \\[ 5pt ] \end{eqnarray}
\] であり，各相が分担する抵抗は\( \ \displaystyle \frac {R_{0}}{3}=\frac {10}{3} \ \mathrm {[\Omega ]} \ \)であるから，これを一次側に換算した抵抗値\( \ \displaystyle R \ \mathrm {[k\Omega ]} \ \)は，ワンポイント解説「1.変圧器の巻数比と変圧比，変流比の関係」の通り，
\[
\begin{eqnarray}
R&=&a^{2}\cdot \frac {R_{0}}{3} \\[ 5pt ] &=&60^{2}\times \frac {10}{3} \\[ 5pt ] &=&12 \ 000 \ \mathrm {[\Omega ]}　→　12.0 \ \mathrm {[k\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。