《機械》〈電動機応用〉[H21:問10]誘導電動機によって回転する送風機のシステムに関する空欄穴埋問題

【問題】

【難易度】★★★★☆（やや難しい）

誘導電動機によって回転する送風機のシステムで消費される電力を考える。

誘導電動機が商用交流電源で駆動されているときに送風機の風量を下げようとする場合，通風路にダンパなどを追加して流路抵抗を上げる方法が一般的である。ダンパの種類などによって消費される電力の減少量は異なるが，流路抵抗を上げ風量を下げるに従って消費される電力は若干減少する。このとき，例えば風量を最初の\( \ 50 \ \mathrm {[％]} \ \)に下げた場合に，誘導電動機の回転速度は\( \ \fbox {　 （ア） 　} \ \)。

一方，商用交流電源で直接駆動するのではなく，出力する交流の電圧\( \ V \ \)と周波数\( \ f \ \)との比\( \ \displaystyle \left( \frac {V}{f}\right) \ \)をほぼ一定とするインバータを用いて，誘導電動機を駆動する周波数を変化させ風量を調整する方法もある。この方法では，ダンパなどの流路抵抗を調整する手段は用いないものとする。このとき，機械的・電気的な損失などが無視できるとすれば，風量は回転速度の\( \ \fbox {　 （イ） 　} \ \)乗に比例し，消費される電力は回転速度の\( \ \fbox {　 （ウ） 　} \ \)乗に比例する。したがって，周波数を変化させて風量を最初の\( \ 50 \ \mathrm {[％]} \ \)に下げた場合に消費される電力は，計算上で\( \ \fbox {　 （エ） 　} \ \mathrm {[％]} \ \)まで減少する。

商用交流電源で駆動し，ダンパなどを追加して風量を下げた場合の消費される電力の減少量はこれほど大きくはなく，インバータを用いると大きな省エネルギー効果が得られる。

上記の記述中の空白箇所(ア)，(イ)，(ウ)及び(エ)に当てはまる語句又は数値として，正しいものを組み合わせたのは次のうちどれか。
\[
\begin{array}{ccccc}
& （ア） & （イ） & （ウ） & （エ） \\
\hline
(1) & 　\displaystyle {トルク変動に相当する滑り周波数分}\atop \displaystyle {だけ変動する　　　　　　　　}　 & 　1　 & 　3　 & 　12.5　 \\
\hline
(2) & 　風量に比例して減少する　　　　　 & 　\displaystyle \frac {1}{2}　 & 　3　 & 　12.5　 \\
\hline
(3) & 　風量に比例して減少する　　　　　 & 　1　 & 　3　 & 　12.5　 \\
\hline
(4) & 　\displaystyle {トルク変動に相当する滑り周波数分}\atop \displaystyle {だけ変動する　　　　　　　　}　 & 　\displaystyle \frac {1}{2}　 & 　2　 & 　25　 \\
\hline
(5) & 　風量に比例して減少する　　　　　 & 　1　 & 　2　 & 　25　 \\
\hline
\end{array}
\]

【ワンポイント解説】

送風機の風量変化時の回転速度や消費電力を検討する問題です。
電験のテキストでは送風機自体の内容はほぼ掲載されていないと考えられますので，風力発電や誘導電動機の内容から答えを導出するようにしましょう。

1.風力発電所の出力
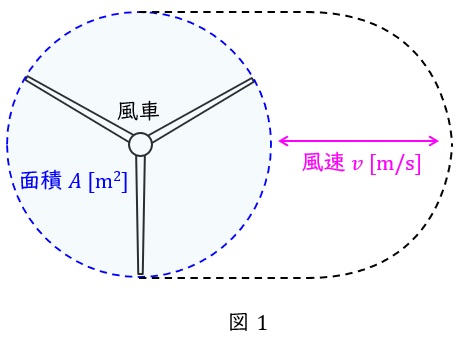
図1に示すように，風車の受風面積を\( \ A \ \mathrm {[m^{2}]} \ \)，風速を\( \ v \ \mathrm {[m／s]} \ \)とすると，単位時間当たりに通過する風の体積\( \ V \ \mathrm {[m^{3}／s]} \ \)は，
\[
\begin{eqnarray}
V &=&Av \ \mathrm {[m^{3}／s]} \\[ 5pt ] \end{eqnarray}
\] となります。したがって，単位時間当たりに通過する風の質量\( \ m \ \mathrm {[kg／s]} \ \)は，空気の密度を\( \ \rho \ \mathrm {[kg／m^{3}]} \ \)とすると，
\[
\begin{eqnarray}
m &=&\rho V \\[ 5pt ] &=&\rho Av \ \mathrm {[kg／s]} \\[ 5pt ] \end{eqnarray}
\] となります。物体の運動エネルギーは\(\displaystyle E=\frac {1}{2}mv^{2}\)であるので，単位時間当たりの風のエネルギー（≒出力）\( \ P \ \mathrm {[W]} \ \)は，
\[
\begin{eqnarray}
P &=&\frac {1}{2}mv^{2} \\[ 5pt ] &=&\frac {1}{2}\rho Av^{3} \ \mathrm {[W]}\\[ 5pt ] \end{eqnarray}
\] と求められます。

2.二次入力\( \ P_{2} \ \)と出力\( \ P_{\mathrm {o}} \ \)と二次銅損\( \ P_{\mathrm {c2}} \ \)の関係
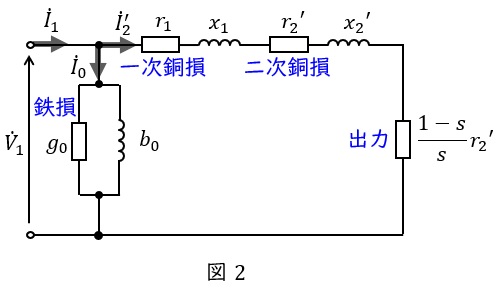
誘導電動機の\( \ \mathrm {L} \ \)形等価回路は図2のようになります。図2において，\( \ {\dot V}_{1} \ \mathrm {[V]} \ \)は一次側端子電圧，\( \ {\dot I}_{1} \ \mathrm {[A]} \ \)は一次電流，\( \ {\dot I}_{2}^{\prime } \ \mathrm {[A]} \ \)は二次電流の一次換算，\( \ {\dot I}_{0} \ \mathrm {[A]} \ \)は励磁電流，\( \ r_{1} \ \mathrm {[\Omega ]} \ \)は一次巻線抵抗，\( \ r_{2}^{\prime } \ \mathrm {[\Omega ]} \ \)は二次巻線抵抗の一次換算，\( \ x_{1} \ \mathrm {[\Omega ]} \ \)は一次漏れリアクタンス，\( \ x_{2}^{\prime } \ \mathrm {[\Omega ]} \ \)は二次漏れリアクタンスの一次換算，\( \ s \ \)は滑りとなります。
図2より，出力\( \ P_{\mathrm {o}} \ \mathrm {[W]} \ \)，二次銅損\( \ P_{\mathrm {c2}} \ \mathrm {[W]} \ \)，二次入力\( \ P_{2} \ \mathrm {[W]} \ \)は，
\[
\begin{eqnarray}
P_{\mathrm {o}} &=& 3\frac {1-s}{s}r_{2}^{\prime }{I_{2}^{\prime }}^{2} \\[ 5pt ] P_{\mathrm {c2}} &=& 3r_{2}^{\prime }{I_{2}^{\prime }}^{2} \\[ 5pt ] P_{2} &=& P_{\mathrm {o}}+P_{\mathrm {c2}} =3\frac {r_{2}^{\prime }}{s}{I_{2}^{\prime }}^{2} \\[ 5pt ] \end{eqnarray}
\] となり，誘導電動機の二次入力\( \ P_{2} \ \mathrm {[W]} \ \)，出力\( \ P_{\mathrm {o}} \ \mathrm {[W]} \ \)，二次銅損\( \ P_{\mathrm {c2}} \ \mathrm {[W]} \ \)には，
\[
\begin{eqnarray}
P_{2}：P_{\mathrm {o}}：P_{\mathrm {c2}} &=& 1：(1-s)：s \\[ 5pt ] \end{eqnarray}
\] の関係があることが分かります。

3.誘導電動機のトルク\( \ T \ \)
図2より，
\[
\begin{eqnarray}
I_{2}^{\prime } &=& \frac {V_{1}}{\displaystyle \sqrt{\left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2}}} \\[ 5pt ] \end{eqnarray}
\] となるから，二次入力\( \ P_{2} \ \mathrm {[W]} \ \)は，
\[
\begin{eqnarray}
P_{2}&=&3\frac {r_{2}^{\prime}}{s}{I^{\prime}_{2}}^{2} \\[ 5pt ] &=&3\frac {r_{2}^{\prime}}{s}\cdot \left( {\frac {V_{1}}{\displaystyle \sqrt{\left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2}}}}\right) ^{2} \\[ 5pt ] &=&\frac {3r_{2}^{\prime}}{s}\cdot \frac {V_{1}^{2}}{\displaystyle \left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2}}
\end{eqnarray}
\] となり，発生するトルク\( \ T \ \mathrm {[N\cdot m]} \ \)は，
\[
\begin{eqnarray}
T&=&\frac {P_{\mathrm {o}}}{\omega } \\[ 5pt ] &=&\frac {(1-s)P_{2}}{(1-s)\omega _{\mathrm {s}}} \\[ 5pt ] &=&\frac {P_{2}}{\omega _{\mathrm {s}}} \\[ 5pt ] &=&\frac {3r_{2}^{\prime}}{\omega _{\mathrm {s}}s}\cdot \frac {V_{1}^{2}}{\displaystyle \left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2}} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(1)
(ア)
回転速度\( \ N \ \mathrm {[{min}^{-1}]} \ \)と同期速度\( \ N_{\mathrm {s}} \ \mathrm {[{min}^{-1}]} \ \)の関係は，極数\( \ p \ \)，周波数を\( \ f \ \mathrm {[Hz]} \ \)とすると\( \ \ \displaystyle N=N_{\mathrm {s}}\left( 1-s\right) =\frac {120f}{p}\left( 1-s\right) \ \)であり，ワンポイント解説「3.誘導電動機のトルク\( \ T \ \)」の通り，誘導電動機のトルク\( \ T \ \mathrm {[N\cdot m]} \ \)は，滑り\( \ s \ \)が\( \ 1 \ \)より十分に小さいとすれば，
\[
\begin{eqnarray}
T&≃&\frac {3r_{2}^{\prime}}{\omega _{\mathrm {s}}s}\cdot \frac {V_{1}^{2}}{\displaystyle \left( \frac {r_{2}^{\prime}}{s}\right) ^{2} } \\[ 5pt ] &=&\frac {3}{\omega _{\mathrm {s}}}\cdot \frac {V_{1}^{2}}{\displaystyle \frac {r_{2}^{\prime}}{s}} \\[ 5pt ] &=&\frac {3V_{1}^{2}s}{\omega _{\mathrm {s}}r_{2}^{\prime}} \\[ 5pt ] &∝&s \\[ 5pt ] \end{eqnarray}
\] となり，トルク\( \ T \ \)と滑り\( \ s \ \)はほぼ比例するため，誘導電動機の回転速度はトルク変動に相当する滑り周波数分だけ変動することになります。

(イ)
一般に風量は回転速度の\( \ 1 \ \)乗に比例します。ファンが回転し空気を切る動きがそのまま風になるとイメージすれば，比例することがイメージできるかと思います。

(ウ)
ワンポイント解説「1.風力発電所の出力」の通り，風力発電における出力は風速の\( \ 3 \ \)乗に比例するため，送風機においても消費される電力は風量の\( \ 3 \ \)乗に比例することになります。また，(イ)の通り風量は回転速度に比例するため，消費される電力は回転速度の\( \ 3 \ \)乗に比例することになります。

(エ)
消費される電力は風量の\( \ 3 \ \)乗に比例するため，風量を最初の\( \ 50 \ \mathrm {[％]} \ \)に下げた場合に消費される電力は，
\[
\begin{eqnarray}
0.5^{3}&=&0.125　→　12.5 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] となります。