Contents
【問題】
【難易度】★★☆☆☆(やや易しい)
二つのビットパターン\( \ 1101 \ \)と\( \ 1011 \ \)のビットごとの論理演算を行う。排他的論理和\( \ \left( \mathrm {ExOR} \right) \ \)は\( \ \fbox { (ア) } \ \),否定論理和\( \ \left( \mathrm {NOR} \right) \ \)は\( \ \fbox { (イ) } \ \)であり,\( \ \fbox { (ア) } \ \)と\( \ \fbox { (イ) } \ \)との論理和\( \ \left( \mathrm {OR} \right) \ \)は\( \ \fbox { (ウ) } \ \)である。\( \ 1011 \ \)と\( \ \fbox { (ウ) } \ \)との排他的論理和\( \ \left( \mathrm {ExOR} \right) \ \)の結果を\( \ 2 \ \)進数と考え,その数値を\( \ 16 \ \)進数で表すと\( \ \fbox { (エ) } \ \)である。
上記の記述中の空白箇所(ア)~(エ)に当てはまる組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
\[
\begin{array}{ccccc}
& (ア) & (イ) & (ウ) & (エ) \\
\hline
(1) & 1001 & 0110 & 1001 & 9 \\
\hline
(2) & 0110 & 0000 & 1111 & \mathrm {D} \\
\hline
(3) & 1001 & 1111 & 1001 & \mathrm {F} \\
\hline
(4) & 0110 & 1111 & 1001 & 9 \\
\hline
(5) & 0110 & 0000 & 0110 & \mathrm {D} \\
\hline
\end{array}
\]
【ワンポイント解説】
ビット毎の論理演算を行ってから\( \ 16 \ \)進数を求める問題です。
電験では各論理回路の真理値表は頭に入れておいた上で論理回路演算を素早く行う必要があります。いろいろなパターンの類題も多く出題されている内容なので,確実に習得しておきましょう。
全く同じではありませんが,平成29年問14に同じ形式の問題が出題されていますので,合わせて学習されると効果的かと思います。
1.主な論理回路の真理値表
基本的な論理回路と図記号は覚える必要がありますので,以下の真理値表を覚えておきましょう。
①\( \ \mathrm {AND} \ \)回路
論理積といい,すべての入力が\( \ 1 \ \)の時のみ\( \ 1 \ \)が出力される回路で,真理値表と図記号は以下の通りです。
\[
\begin{array}{cc|c}
\mathrm {A} & \mathrm {B} & 出力 \\
\hline
0 & 0 & 0 \\
0 & 1 & 0 \\
1 & 0 & 0 \\
1 & 1 & 1 \\
\end{array}
\]

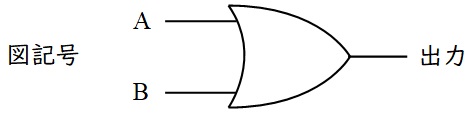
②\( \ \mathrm {OR} \ \)回路
論理和といい,入力が一つでも\( \ 1 \ \)の時\( \ 1 \ \)が出力される回路で,真理値表と図記号は以下の通りです。
\[
\begin{array}{cc|c}
\mathrm {A} & \mathrm {B} & 出力 \\
\hline
0 & 0 & 0 \\
0 & 1 & 1 \\
1 & 0 & 1 \\
1 & 1 & 1 \\
\end{array}
\]
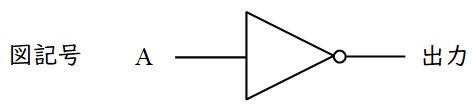
③\( \ \mathrm {NOT} \ \)回路
論理否定といい,入力を反転する回路で,真理値表と図記号は以下の通りです。
\[
\begin{array}{c|c}
\mathrm {A} & 出力 \\
\hline
0 & 1 \\
1 & 0 \\
\end{array}
\]
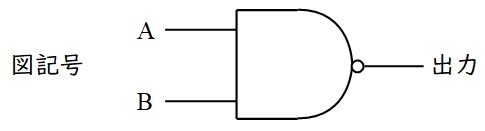
④\( \ \mathrm {NAND} \ \)回路
\( \ \mathrm {NOT}+\mathrm {AND} \ \)で\( \ \mathrm {AND} \ \)の\( \ \mathrm {NOT} \ \)を出力,すなわちすべての入力が\( \ 1 \ \)の時のみ\( \ 0 \ \)が出力される回路で,真理値表と図記号は以下の通りです。
\[
\begin{array}{cc|c}
\mathrm {A} & \mathrm {B} & 出力 \\
\hline
0 & 0 & 1 \\
0 & 1 & 1 \\
1 & 0 & 1 \\
1 & 1 & 0 \\
\end{array}
\]
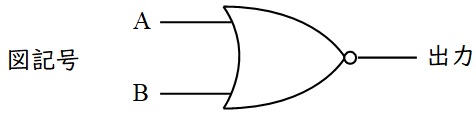
⑤\( \ \mathrm {NOR} \ \)回路
\( \ \mathrm {NOT}+\mathrm {OR} \ \)で\( \ \mathrm {OR} \ \)の\( \ \mathrm {NOT} \ \)を出力,すなわち入力が一つでも\( \ 1 \ \)の時\( \ 0 \ \)が出力される回路で,真理値表と図記号は以下の通りです。
\[
\begin{array}{cc|c}
\mathrm {A} & \mathrm {B} & 出力 \\
\hline
0 & 0 & 1 \\
0 & 1 & 0 \\
1 & 0 & 0 \\
1 & 1 & 0 \\
\end{array}
\]
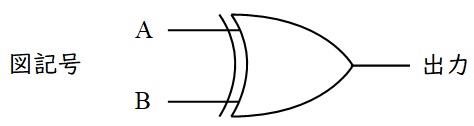
⑥\( \ \mathrm {ExOR} \ \)回路
排他的論理和\( \ \left( \mathrm {exclusive \ or} \right) \ \)といい,入力が異なるとき\( \ 1 \ \),入力が同じ時\( \ 0 \ \)が出力される回路で,真理値表と図記号は以下の通りです。
\[
\begin{array}{cc|c}
\mathrm {A} & \mathrm {B} & 出力 \\
\hline
0 & 0 & 0 \\
0 & 1 & 1 \\
1 & 0 & 1 \\
1 & 1 & 0 \\
\end{array}
\]
2.主な進数の対応表
コンピュータ等のディジタル信号は主に\( \ 2 \ \)進数が使用されるため,電験でも基数変換は出題されます。
電験で出題される\( \ 2 \ \)進数,\( \ 8 \ \)進数,\( \ 10 \ \)進数,\( \ 16 \ \)進数の対応表は下表の通りとなります。表を覚えるのではなくルールを理解するようにしましょう。
\[
\begin{array}{|r|r|r|r|}
\hline
2 \ 進数 & 8 \ 進数 & 10 \ 進数 & 16 \ 進数 \\
\hline
0 & 0 & 0 & 0 \\
\hline
1 & 1 & 1 & 1 \\
\hline
10 & 2 & 2 & 2 \\
\hline
11 & 3 & 3 & 3 \\
\hline
100 & 4 & 4 & 4 \\
\hline
101 & 5 & 5 & 5 \\
\hline
110 & 6 & 6 & 6 \\
\hline
111 & 7 & 7 & 7 \\
\hline
1000 & 10 & 8 & 8 \\
\hline
1001 & 11 & 9 & 9 \\
\hline
1010 & 12 & 10 & \mathrm {A} \\
\hline
1011 & 13 & 11 & \mathrm {B} \\
\hline
1100 & 14 & 12 & \mathrm {C} \\
\hline
1101 & 15 & 13 & \mathrm {D} \\
\hline
1110 & 16 & 14 & \mathrm {E} \\
\hline
1111 & 17 & 15 & \mathrm {F} \\
\hline
10000 & 20 & 16 & 10 \\
\hline
\end{array}
\]
3.\( \ 10 \ \)進数から\( \ 2 \ \)進数への変換
\( \ 10 \ \)進数から\( \ 2 \ \)進数への変換は,\( \ 2 \ \)で割った余りを下から順に並べると求められます。
具体的に\( \ 10 \ \)進数の\( \ \left( 30\right) _{10} \ \)を\( \ 2 \ \)進数へ変換すると,
\[
\begin{array}{cccc}
2) & 30 & & & \\
\hline
2) & 15 & \cdots & 0 \\
\hline
2) & 7 & \cdots & 1 \\
\hline
2) & 3 & \cdots & 1 \\
\hline
2) & 1 & \cdots & 1 \\
\hline
& 0 & \cdots & 1 \\
\end{array}
\]
ゆえに,
\[
\begin{eqnarray}
\left( 30\right) _{10} &=&\left( 11110\right) _{2} \\[ 5pt ]
\end{eqnarray}
\]
となります。\( \ 8 \ \)進数や\( \ 16 \ \)進数への変換も同様に行うことができます。
4.\( \ 2 \ \)進数から\( \ 10 \ \)進数への変換
\( \ 2 \ \)進数を\( \ 10 \ \)進数にするためには各桁に\( \ 2^{x}(x=0,1,2・・・) \ \)乗をかけて導出できます。
例えば,\( \ 2 \ \)進数の\( \ \left( 101010\right) _{2} \ \)を\( \ 10 \ \)進数へ変換すると,
\[
\begin{eqnarray}
\left( 101010\right) _{2}&=&1\times 2^{5}+0\times 2^{4}+1\times 2^{3}+0\times 2^{2}+1\times 2^{1}+0\times 2^{0} \\[ 5pt ]
&=&32+0+8+0+2+0 \\[ 5pt ]
&=&42 \\[ 5pt ]
\end{eqnarray}
\]
と求められます。\( \ 8 \ \)進数や\( \ 16 \ \)進数も同様に求められます。
5.\( \ 2 \ \)進数から\( \ 16 \ \)進数への変換
\( \ 2 \ \)進数を\( \ 16 \ \)進数にするためには,\( \ 4 \ \)桁ごとに\( \ 16 \ \)進数に変換していきます。
例えば,\( \ 2 \ \)進数の\( \ \left( 11011010\right) _{2} \ \)を\( \ 16 \ \)進数へ変換すると,
\[
\begin{eqnarray}
\left( 1101\right) _{2}&=&\left( \mathrm {D}\right) _{16} \\[ 5pt ]
\left( 1010\right) _{2}&=&\left( \mathrm {A}\right) _{16} \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
\left( 11011010\right) _{2}&=&\left( \mathrm {DA}\right) _{16} \\[ 5pt ]
\end{eqnarray}
\]
と求められます。\( \ 16 \ \)進数から\( \ 2 \ \)進数への変換も逆の操作により求めることができます。
【解答】
解答:(5)
(ア)
ワンポイント解説「1.主な論理回路の真理値表」の通り,\( \ 1101 \ \)と\( \ 1011 \ \)のビットごとの排他的論理和\( \ \left( \mathrm {ExOR} \right) \ \)は,ビット毎に同符号であれば\( \ 0 \ \),異符号であれば\( \ 1 \ \)を出力するので,\( \ 0110 \ \)となります。
(イ)
ワンポイント解説「1.主な論理回路の真理値表」の通り,\( \ 1101 \ \)と\( \ 1011 \ \)のビットごとの否定論理和\( \ \left( \mathrm {NOR} \right) \ \)は,どちらか一方でも\( \ 1 \ \)であれば\( \ 0 \ \)を出力するので,\( \ 0000 \ \)となります。
(ウ)
ワンポイント解説「1.主な論理回路の真理値表」の通り,(ア)\( \ 0110 \ \)と(イ)\( \ 0000 \ \)のビットごとの論理和\( \ \left( \mathrm {OR} \right) \ \)は,どちらか一方でも\( \ 1 \ \)であれば\( \ 1 \ \)を出力するので,\( \ 0110 \ \)となります。
(エ)
ワンポイント解説「1.主な論理回路の真理値表」の通り,\( \ 1011 \ \)と(ウ)\( \ 0110 \ \)のビットごとの排他的論理和\( \ \left( \mathrm {ExOR} \right) \ \)は,ビット毎に同符号であれば\( \ 0 \ \),異符号であれば\( \ 1 \ \)を出力するので,\( \ 1101 \ \)となります。これを\( \ 16 \ \)進数で表すと,ワンポイント解説「2.主な進数の対応表」の通り\( \ \mathrm {D} \ \)となります。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは