《機械》〈変圧器〉[H24:問7]単相変圧器のリアクタンスの大きさに関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

単相変圧器があり，二次側を開放して電流を流さない場合の二次電圧の大きさを\( \ 100 \ \mathrm {[％]} \ \)とする。二次側にリアクトルを接続して力率\( \ 0 \ \)の電流を流した場合，二次電圧は\( \ 5 \ \mathrm {[％]} \ \)下がって\( \ 95 \ \mathrm {[％]} \ \)であった。二次側に抵抗器を接続して，前述と同じ大きさの力率\( \ 1 \ \)の電流を流した場合，二次電圧は\( \ 2 \ \mathrm {[％]} \ \)下がって\( \ 98 \ \mathrm {[％]} \ \)であった。一次巻線抵抗と一次換算した二次巻線抵抗との和は\( \ 10 \ \mathrm {[\Omega ]} \ \)である。鉄損及び励磁電流は小さく，無視できるものとする。ベクトル図を用いた電圧変動率の計算によく用いられる近似計算を利用して，一次漏れリアクタンスと一次換算した二次漏れリアクタンスとの和\( \ \mathrm {[\Omega ]} \ \)の値を求めた。その値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 5 \ \)　　(2)　\( \ 10 \ \)　　(3)　\( \ 15 \ \)　　(4)　\( \ 20 \ \)　　(5)　\( \ 25 \ \)

【ワンポイント解説】

変圧器の問題は等価回路が描けないとスタートラインに立つことができません。また，電圧降下の近似式もベクトル図を思い出しながらで良いですが，基本的には覚える必要があります。計算も多く，やや難しめの問題ですが，重要な内容を多く含む問題なので，よく理解するようにしましょう。

1.変圧器の等価回路（一次換算）
変圧器の一次側等価回路を図1に示します。ただし，\( \ {\dot V}_{1} \ \)は一次側端子電圧，\( \ {\dot I}_{1} \ \)は一次電流，\( \ {\dot I}_{2} \ \)は二次電流，\( \ {\dot I}_{0} \ \)は励磁電流，\( \ r_{1} \ \)は一次巻線抵抗，\( \ r_{2} \ \)は二次巻線抵抗，\( \ x_{1} \ \)は一次漏れリアクタンス，\( \ x_{2} \ \)は二次漏れリアクタンス，\( \ a \ \)は変圧比（巻数比）となります。

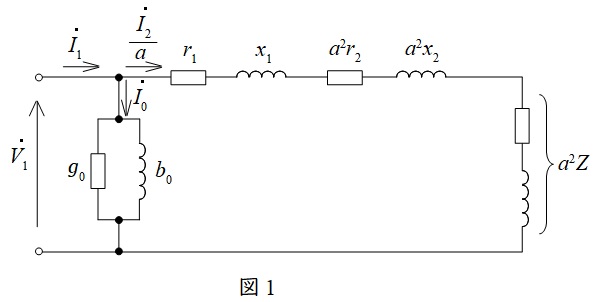
2.電圧降下の近似式
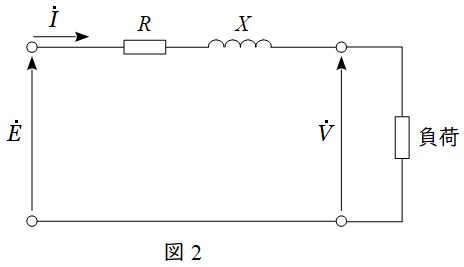
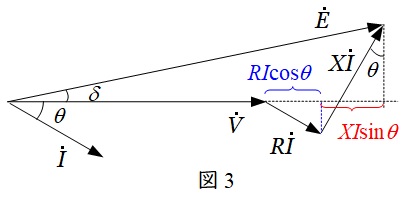
図2のような回路において，ベクトル図を描くと図3のようになります。
図3のベクトル図において，\(\dot E \)と\(\dot V\)の位相差が十分に小さいと仮定すると，線路の電圧降下\(\varepsilon =E-V\)は，
\[
\begin{eqnarray}
E&≃&V+RI\cos \theta +XI\sin \theta \\[ 5pt ] E-V&=&RI\cos \theta +XI\sin \theta \\[ 5pt ] \varepsilon &=&I\left( R\cos \theta +X\sin \theta \right) \\[ 5pt ] \end{eqnarray}
\] と求められます。

【解答】

解答：(5)
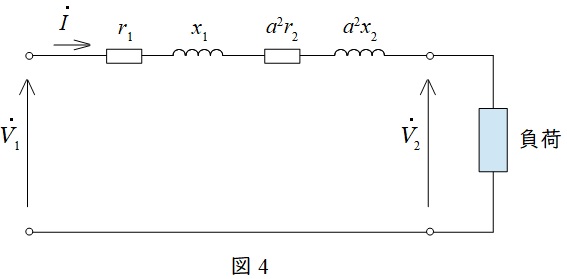
題意より励磁回路は無視できるので，本問の等価回路は図4のように描ける。
図4より，二次側を開放した時は回路に電流が流れないので，電圧降下は\( \ 0 \ \)となるので，\( \ {\dot V}_{1}={\dot V}_{2}→100 \ \mathrm {[％]} \ \)となる。
リアクトル\( \ x \ \)を接続したとき，電圧降下\( \ \varepsilon \ \)は，回路に流れる電流を\( \ I_{1} \ \)とすると，ワンポイント解説「2.電圧降下の近似式」より，
\[
\begin{eqnarray}
\varepsilon &=&I_{1}\left\{ \left( r_{1} +a^{2}r_{2}\right) \cos \theta +\left( x_{1} +a^{2}x_{2}\right) \sin \theta \right\} \\[ 5pt ] \end{eqnarray}
\] となり，\( \ \varepsilon =0.05V_{2}=0.05V_{1} \ \)，\( \ \displaystyle \theta =\frac {\pi }{2} \ \)であるから，
\[
\begin{eqnarray}
0.05V_{1} &=&I_{1}\left\{ \left( r_{1} +a^{2}r_{2}\right) \cos \frac {\pi }{2} +\left( x_{1} +a^{2}x_{2}\right) \sin \frac {\pi }{2} \right\} \\[ 5pt ] &=&I_{1}\left\{ \left( r_{1} +a^{2}r_{2}\right) \times 0 +\left( x_{1} +a^{2}x_{2}\right) \times 1 \right\} \\[ 5pt ] &=&\left( x_{1} +a^{2}x_{2}\right) I_{1} 　・・・・・・・・・　① \\[ 5pt ] \end{eqnarray}
\] となる。同様に，抵抗\( \ r \ \)を接続したとき，電圧降下\( \ \varepsilon \ \)は，回路に流れる電流を\( \ I_{2} \ \)とすると，
\[
\begin{eqnarray}
\varepsilon &=&I_{2}\left\{ \left( r_{1} +a^{2}r_{2}\right) \cos \theta +\left( x_{1} +a^{2}x_{2}\right) \sin \theta \right\} \\[ 5pt ] \end{eqnarray}
\] となり，\( \ \varepsilon =0.02V_{2}=0.02V_{1} \ \)，\( \ \displaystyle \theta =0 \ \)であるから，
\[
\begin{eqnarray}
0.02V_{1} &=&I_{2}\left\{ \left( r_{1} +a^{2}r_{2}\right) \cos 0 +\left( x_{1} +a^{2}x_{2}\right) \sin 0 \right\} \\[ 5pt ] &=&I_{2}\left\{ \left( r_{1} +a^{2}r_{2}\right) \times 1 +\left( x_{1} +a^{2}x_{2}\right) \times 0 \right\} \\[ 5pt ] &=&\left( r_{1} +a^{2}r_{2}\right) I_{2} \\[ 5pt ] \end{eqnarray}
\] となる。題意より，\( \ I_{1} =I_{2} \ \)，\( \ r_{1} +a^{2}r_{2}=10 \ \mathrm {[\Omega ]} \ \)であるから，
\[
\begin{eqnarray}
0.02V_{1} &=&10 I_{1} \\[ 5pt ] V_{1} &=&500 I_{1} \\[ 5pt ] \end{eqnarray}
\] と整理できる。これを①式に代入すると，
\[
\begin{eqnarray}
0.05V_{1}&=&\left( x_{1} +a^{2}x_{2}\right) I_{1} \\[ 5pt ] 0.05\times 500 I_{1}&=&\left( x_{1} +a^{2}x_{2}\right) I_{1} \\[ 5pt ] 25 I_{1}&=&\left( x_{1} +a^{2}x_{2}\right) I_{1} \\[ 5pt ] x_{1} +a^{2}x_{2}&=&25 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。