《機械》〈情報伝送及び処理〉[H25:問18]ブール代数に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

論理関数に関する次の(a)及び(b)の問に答えよ。

(a)　論理式\( \ X\cdot Y\cdot \overline Z + X\cdot Y\cdot Z+ \overline X\cdot Y\cdot Z +\overline X\cdot \overline Y\cdot Z \ \)を積和形式で簡略化したものを次の(1)～(5)のうちから一つ選べ。

　(1)　\(X\cdot Y+X\cdot Z\)　　(2)　\(X\cdot \overline Y+Y\cdot Z\)　　(3)　\(\overline X\cdot Y+X\cdot Z\)
　(4)　\(X\cdot Y+\overline Y\cdot Z\)　　(5)　\(X\cdot Y+\overline X\cdot Z\)

(b)　論理式\( \ ( X+Y+Z) \cdot ( X+\overline Y+Z) \cdot ( \overline X+Y+Z) \ \)を和積形式で簡略化したものを次の(1)～(5)のうちから一つ選べ。

　(1)　\(( X+Z) \cdot ( \overline Y+Z) \)　(2)　\(( \overline X+Y) \cdot ( X+Z) \)　(3)　\(( X+Y) \cdot ( Y+Z) \)
　(4)　\(( X+Z) \cdot ( Y+Z) \)　(5)　\(( X+Y) \cdot ( \overline X+Z) \)

【ワンポイント解説】

ブール代数の簡略化に関する問題ですが，基本的には法則を丸暗記することはあまりオススメしません。いろいろな問題を解くことにより，ブール代数の法則は何となく理解できるようになります。どうしてもわからない場合は論理式に関する図を作図して，どの解答が正答かを求めるのが良いと思います。((b)で例を示します。)

1.ブール代数の法則
ブール代数の法則は以下の表に示すように，様々なものがあります。一般的な数式と似ているものが多いので，私もしっかりと覚えているのはド・モルガンの定理ぐらいです。基本的には覚えるよりも理解する方が大事であると思います。
\[
\begin{array}{|c|c|}
\hline
同一則 & A\cdot A=A　A+A=A　\\
\hline
補元則 & A\cdot \overline A=0　A+\overline A=1　\\
\hline
復元則 & \overline {\overline A}=A　\\
\hline
交換則 & A\cdot B=B\cdot A　A+B=B+A \\
\hline
結合則 & A\cdot (B\cdot C)=(A\cdot B)\cdot C　A+(B+C)=(A+B)+C \\
\hline
分配則 & A\cdot (B+C)=A\cdot B+A\cdot C　(A+B)\cdot (A+C)=A+B\cdot C \\
\hline
吸収則 & {\displaystyle A\cdot (A+B)=A　A+A\cdot B=A} \atop {\displaystyle A+\overline A \cdot B=A+B　\overline A+ A \cdot B=\overline A+B} \\
\hline
ド・モルガンの定理 & \overline {A+B}=\overline A \cdot \overline B　\overline {A\cdot B}=\overline A + \overline B \\
\hline
\end{array}
\]

【解答】

(a)解答：(5)
論理式\( \ X\cdot Y\cdot \overline Z + X\cdot Y\cdot Z+ \overline X\cdot Y\cdot Z +\overline X\cdot \overline Y\cdot Z \ \)をワンポイント解説「1.ブール代数の法則」に沿って整理すると，
\[
\begin{eqnarray}
&&X\cdot Y\cdot \overline Z + X\cdot Y\cdot Z+ \overline X\cdot Y\cdot Z +\overline X\cdot \overline Y\cdot Z && \\[ 5pt ] &=& X\cdot (Y\cdot \overline Z + Y\cdot Z)+ \overline X \cdot ( Y\cdot Z +\overline Y\cdot Z )　&(分配則)& \\[ 5pt ] &=& X\cdot Y \cdot (\overline Z + Z)+ \overline X \cdot ( Y +\overline Y ) \cdot Z　&(分配則)& \\[ 5pt ] &=& X\cdot Y \cdot 1+ \overline X \cdot 1 \cdot Z　&(補元則)& \\[ 5pt ] &=& X\cdot Y + \overline X \cdot Z　&(吸収則)& \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(4)
論理式\( \ ( X+Y+Z) \cdot ( X+\overline Y+Z) \cdot ( \overline X+Y+Z) \ \)をワンポイント解説「1.ブール代数の法則」に沿って整理すると，
\[
\begin{eqnarray}
&&( X+Y+Z) \cdot ( X+\overline Y+Z) \cdot ( \overline X+Y+Z) && \\[ 5pt ] &=& ( X+Y) \cdot ( X+\overline Y) \cdot ( \overline X+Y)+Z　&(分配則)& \\[ 5pt ] &=& (X+ Y \cdot \overline Y) \cdot ( \overline X+Y)+Z　&(分配則)& \\[ 5pt ] &=& (X+ 0) \cdot ( \overline X+Y)+Z　&(補元則)& \\[ 5pt ] &=& X \cdot ( \overline X+Y)+Z　&(吸収則)& \\[ 5pt ] &=& X \cdot \overline X+X\cdot Y+Z　&(分配則)& \\[ 5pt ] &=& 0+X\cdot Y+Z　&(補元則)& \\[ 5pt ] &=& X\cdot Y+Z　&(吸収則)& \\[ 5pt ] &=& (X+Z)\cdot (Y+Z)　&(分配則)& \\[ 5pt ] \end{eqnarray}
\] と求められる。

【別解】
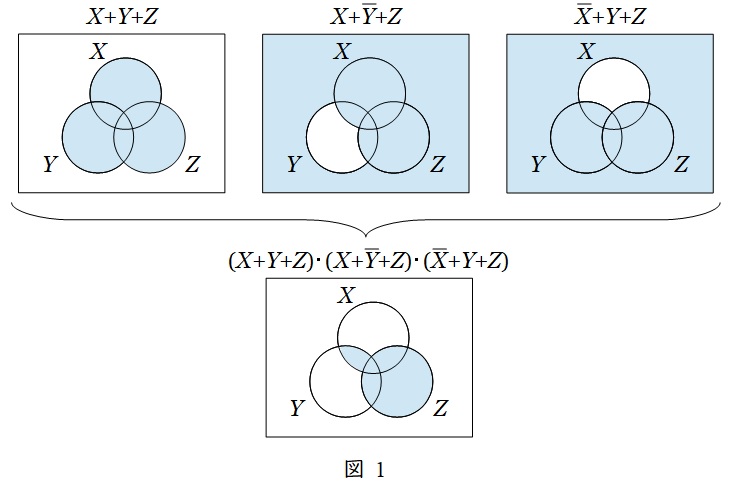
論理式\( \ ( X+Y+Z) \cdot ( X+\overline Y+Z) \cdot ( \overline X+Y+Z) \ \)を図に描くと図1のようになる。
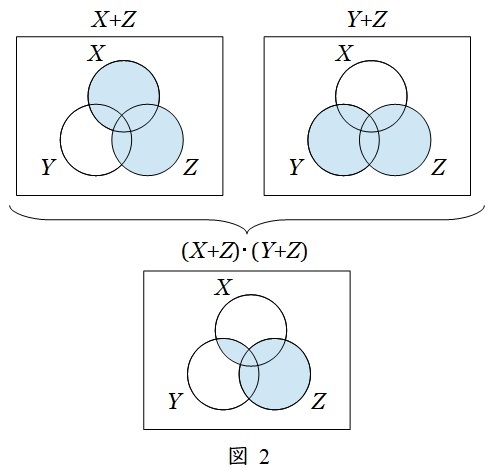
同様に(1)～(5)の論理式を図に描くと，(4)が図2のようになり，\( \ ( X+Y+Z) \cdot ( X+\overline Y+Z) \cdot ( \overline X+Y+Z) \ \)と一致する。