《機械》〈回転機〉[H25:問6]同期発電機の同期インピーダンスに関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】
- 3.1 【本問に関する質疑応答】

【問題】

【難易度】★★☆☆☆（やや易しい）

定格電圧\( \ 6.6 \ \mathrm {[kV]} \ \)，定格電流\( \ 1050 \ \mathrm {[A]} \ \)の三相同期発電機がある。この発電機の短絡比は\( \ 1.25 \ \)である。

この発電機の同期インピーダンス\( \ \mathrm {[\Omega ]} \ \)の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 0.80 \ \)　　(2)　\( \ 2.90 \ \)　　(3)　\( \ 4.54 \ \)　　(4)　\( \ 5.03 \ \)　　(5)　\( \ 7.86 \ \)

【ワンポイント解説】

百分率同期インピーダンスが短絡比の逆数になることを理解していることが重要です。四機の内容の中でも，どうしても暗記が必要な内容ですが，二種や一種になっても出題される内容となりますので，よく理解しておくようにしましょう。

1.同期発電機の短絡比\( \ K_{\mathrm {s}} \ \)
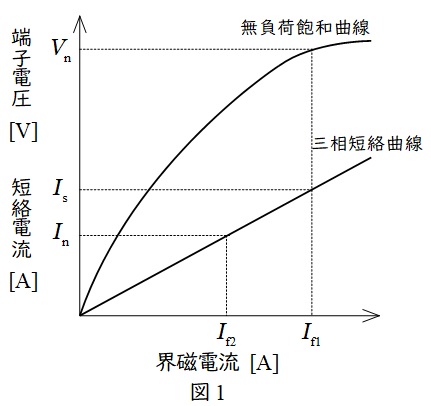
同期発電機は図1のような特性曲線を描くことができます。図1において定格電圧を\( \ V_{\mathrm {n}} \ \)，定格電流を\( \ I_{\mathrm {n}} \ \)とし，定格電圧を誘起するのに必要な界磁電流\( \ I_{\mathrm {f1}} \ \)，\( \ I_{\mathrm {f1}} \ \)における三相短絡電流を\( \ I_{\mathrm {s}} \ \)，定格速度，三相短絡状態で定格電流\( \ I_{\mathrm {n}} \ \)に等しい短絡電流を流すのに必要な界磁電流を\( \ I_{\mathrm {f2}} \ \)とすると，短絡比\( \ K_{\mathrm {s}} \ \)は下式のように求めることができます。
\[
\begin{eqnarray}
K_{\mathrm {s}} &=& \frac {I_{\mathrm {f1}}}{I_{\mathrm {f2}}} \\[ 5pt ] &=& \frac {I_{\mathrm {s}}}{I_{\mathrm {n}}} \\[ 5pt ] \end{eqnarray}
\]

2.同期インピーダンス\( \ Z_{\mathrm {s}} \ \)，百分率同期インピーダンス\( \ ％Z_{\mathrm {s}} \ \)
同期インピーダンス\( \ Z_{\mathrm {s}} \ \)は特性曲線の値から，
\[
\begin{eqnarray}
Z_{\mathrm {s}} &=& \frac {V_{\mathrm {n}}／\sqrt {3}}{I_{\mathrm {s}}} \\[ 5pt ] &=& \frac {V_{\mathrm {n}}}{\sqrt {3}I_{\mathrm {s}}} \\[ 5pt ] \end{eqnarray}
\] で求められ，百分率同期インピーダンス\( \ ％Z_{\mathrm {s}} \ \)は，
\[
\begin{eqnarray}
％Z_{\mathrm {s}} &=& \frac {Z_{\mathrm {s}}I_{\mathrm {n}}}{V_{\mathrm {n}}／\sqrt {3}} \times 100 \\[ 5pt ] &=& \frac {\sqrt {3}Z_{\mathrm {s}}I_{\mathrm {n}}}{V_{\mathrm {n}}} \times 100 \\[ 5pt ] &=& \frac {I_{\mathrm {n}}}{I_{\mathrm {s}}} \times 100 \\[ 5pt ] \end{eqnarray}
\] となります。これより，短絡比\( \ K_{\mathrm {s}} \ \)と百分率同期インピーダンス\( \ ％Z_{\mathrm {s}} \ \)には，
\[
\begin{eqnarray}
K_{\mathrm {s}} &=& \frac {100}{％Z_{\mathrm {s}}} \\[ 5pt ] \end{eqnarray}
\] の関係があります。

【解答】

解答：(2)
ワンポイント解説「2.同期インピーダンス\( \ Z_{\mathrm {s}} \ \)，百分率同期インピーダンス\( \ ％Z_{\mathrm {s}} \ \)」より，百分率同期インピーダンス\( \ ％Z_{\mathrm {s}} \ \)は，
\[
\begin{eqnarray}
K_{\mathrm {s}} &=& \frac {100}{％Z_{\mathrm {s}}} \\[ 5pt ] ％Z_{\mathrm {s}} &=& \frac {100}{K_{\mathrm {s}}} \\[ 5pt ] &=& \frac {100}{1.25} \\[ 5pt ] &=& 80 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] であるから，同期インピーダンス\( \ Z_{\mathrm {s}} \ \)は，
\[
\begin{eqnarray}
％Z_{\mathrm {s}} &=& \frac {\sqrt {3}Z_{\mathrm {s}}I_{\mathrm {n}}}{V_{\mathrm {n}}} \times 100 \\[ 5pt ] Z_{\mathrm {s}}&=& \frac {％Z_{\mathrm {s}}V_{\mathrm {n}}}{100\sqrt {3}I_{\mathrm {n}}} \\[ 5pt ] &=& \frac {80\times 6.6\times 10^{3}}{100\sqrt {3}\times 1050} \\[ 5pt ] &≒& 2.90 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。