《機械》〈情報伝送及び処理〉[H26:問18]非同期式カウンタ回路に関する空欄穴埋問題

【問題】

【難易度】★★★☆☆（普通）

図は\(\mathrm {JK-}\)フリップフロップ( \(\mathrm {FF1}\)，\(\mathrm {FF2}\)，\(\mathrm {FF3}\) )と論理回路\(\mathrm {D}\)を用いた非同期式カウンタ回路とそのタイムチャートである。次の(a)及び(b)の問に答えよ。

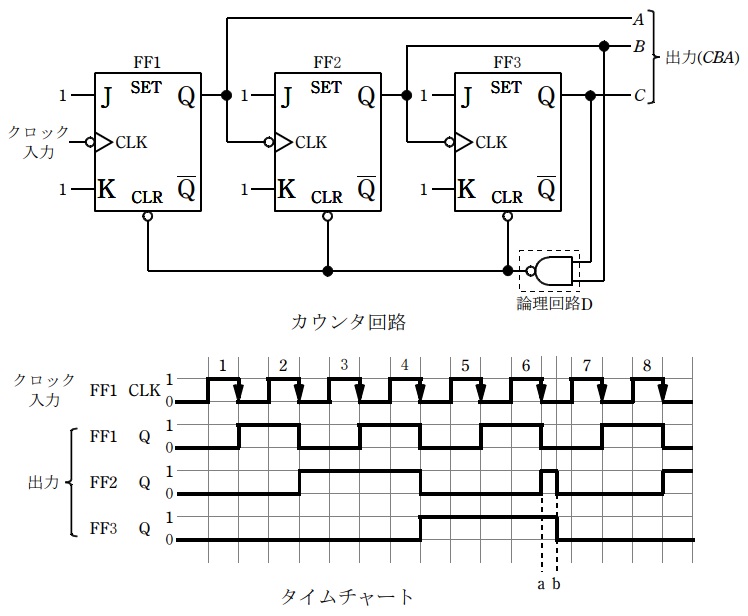
(a)　カウンタ回路における論理回路\(\mathrm {D}\)は，\(\fbox {　 （ア） 　}\)回路で，その役割は出力(\(CBA\) )が2進数でカウンタの最大数\(\fbox {　 （イ） 　}\)になった後，次のクロック入力の立ち下がりによって出力(\(CBA\) )を2進数で\(\fbox {　 （ウ） 　}\)にすることである。

上記の記述中の空白箇所(ア)，(イ)及び(ウ)に当てはまる組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。

\[
\begin{array}{cccc}
& （ア） & （イ） & （ウ） \\
\hline
(1) & \mathrm {NOR} & 101 & 000 \\
\hline
(2) & \mathrm {NOR} & 110 & 111 \\
\hline
(3) & \mathrm {NAND} & 110 & 111 \\
\hline
(4) & \mathrm {NAND} & 110 & 000 \\
\hline
(5) & \mathrm {NAND} & 101 & 000 \\
\hline
\end{array}
\]

(b)　タイムチャートにおいて，クロック入力のパルス6の立ち下がりで\(\mathrm {FF1}\)の\(\mathrm {Q}\)出力は\(1\)から\(0\)へ変化する。\(\mathrm {FF1}\)の立ち下がりは\(\mathrm {FF2}\)を動作させ，\(0\)から\(1\)に変化させる。図の\(\mathrm {a}\)時点で\(\mathrm {FF2}\)及び\(\mathrm {FF3}\)の\(\mathrm {Q}\)出力はともに\(\fbox {　 （ア） 　}\)である。これら二つの\(\fbox {　 （ア） 　}\)は論理回路\(\mathrm {D}\)に入力され，その出力は\(\fbox {　 （イ） 　}\)となる。この\(\fbox {　 （イ） 　}\)は三つの\(\mathrm {JK-}\)フリップフロップの\(\mathrm {CLR}\)入力端子に入って，\(\mathrm {b}\)時点において，クリアされている。\(\mathrm {a}\)時点から\(\mathrm {b}\)時点までの\(\mathrm {FF2}\)の\(\mathrm {Q}\)に現われるパルスは，パルス幅が非常に狭いため，カウンタの出力\(\fbox {　 （ア） 　}\)としてはカウントされない。カウンタは再びカウントを開始する。クロック入力のパルス\(6\)が\(1\)から\(0\)に変化する時刻と，\(\mathrm {FF2}\)及び\(\mathrm {FF3}\)が最終的に\(\mathrm {b}\)時点でクリアされる時刻とには時間遅れが生じている。これは論理回路\(\mathrm {D}\)とフリップフロップの入出力における信号の\(\fbox {　 （ウ） 　}\)遅れに起因している。

上記の記述中の空白箇所(ア)，(イ)及び(ウ)に当てはまる組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。

\[
\begin{array}{cccc}
& （ア） & （イ） & （ウ） \\
\hline
(1) & 1 & 0 & 伝　搬 \\
\hline
(2) & 0 & 1 & 伝　搬 \\
\hline
(3) & 1 & 1 & 伝　搬 \\
\hline
(4) & 0 & 1 & 同　期 \\
\hline
(5) & 1 & 0 & 同　期 \\
\hline
\end{array}
\]

【ワンポイント解説】

論理回路の問題は毎年のように出題されています。フリップフロップの内容は少しマイナーな分野ではありますが、それほど難しいものではないので，理解しておいても良いと思います。

1.\(\mathrm {NAND}\)回路と\(\mathrm {NOR}\)回路
\(\mathrm {NAND}\)回路は二つの入力がともに\(1\)の時のみ\(0\)が出力される回路で，\(\mathrm {NOR}\)回路は二つの入力がともに\(0\)の時のみ\(1\)が出力される回路です。

　表1　\(\mathrm {NAND}\)回路
\[
\begin{array}{c|cc}
{ }_{A}\setminus { }^{B} & 0 & 1 \\
\hline
0 & 1 & 1 \\
1 & 1 & 0 \\
\end{array}
\]

　表2　\(\mathrm {NOR}\)回路
\[
\begin{array}{c|cc}
{ }_{A}\setminus { }^{B} & 0 & 1 \\
\hline
0 & 1 & 0 \\
1 & 0 & 0 \\
\end{array}
\]

【解答】

(a)解答：(5)
(ア)
図の記号は二つの入力がともに\(1\)の時のみ\(0\)が出力される\(\mathrm {NAND}\)回路となります。

(イ)
(ウ)
このカウンタ回路はタイムチャートの通り\(000\)→\(001\)→\(010\)→\(101\)→\(110\)となると，\(\mathrm {C}\)と\(\mathrm {B}\)が\(1\)となり\(\mathrm {NAND}\)回路で\(0\)が出力され，\(000\)となります。よって，題意に沿って解答欄を入れると(イ)が\(101\)，(ウ)が\(000\)となります。

(b)解答：(1)
(ア)
タイムチャートの通り図の\(\mathrm {a}\)時点で\(\mathrm {FF2}\)及び\(\mathrm {FF3}\)の\(\mathrm {Q}\)出力はともに\(1\)となります。

(イ)
\(\mathrm {FF2}\)及び\(\mathrm {FF3}\)が\(1\)となると論理回路\(\mathrm {D}\)は\(\mathrm {NAND}\)回路なので\(0\)が出力されます。

(ウ)
図の\(\mathrm {a}\)から\(\mathrm {b}\)の時間遅れの時間は\(\mathrm {NAND}\)回路から\(\mathrm {CLR}\)までの伝搬遅れとなります。