《機械》〈回転機〉[R01:問5]同期電動機の出力の特性に関する空欄穴埋問題

【問題】

【難易度】★☆☆☆☆（易しい）

次の文章は，星形結線の円筒形三相同期電動機の入力，出力，トルクに関する記述である。

この三相同期電動機の\( \ 1 \ \)相分の誘導起電力\( \ E \ \mathrm {[V]} \ \)，電圧\( \ V \ \mathrm {[V]} \ \)，電流\( \ I \ \mathrm {[A]} \ \)，\( \ V \ \)と\( \ I \ \)の位相差を\( \ \theta \ \mathrm {[rad]} \ \)としたときの\( \ 1 \ \)相分の入力\( \ P_{\mathrm {i}} \ \mathrm {[W]} \ \)は次式で表される。
\[
\begin{eqnarray}
P_{\mathrm {i}} &=&VI\cos \theta \\[ 5pt ] \end{eqnarray}
\] また，\( \ E \ \)と\( \ V \ \)の位相差を\( \ \delta \ \mathrm {[rad]} \ \)とすると，\( \ 1 \ \)相分の出力\( \ P_{\mathrm {o}} \ \mathrm {[W]} \ \)は次式で表される。\( \ E \ \)と\( \ V \ \)の位相差\( \ \delta \ \)は\( \ \fbox {　 （ア） 　} \ \)といわれる。
\[
\begin{eqnarray}
P_{\mathrm {o}} &=&EI\cos \left( \delta – \theta \right) =\frac {VE}{x}\fbox {　 （イ） 　} \\[ 5pt ] \end{eqnarray}
\] ここで，\( \ x \ \mathrm {[\Omega ]} \ \)は同期リアクタンスであり，電機子巻線抵抗は無視できるものとする。

この三相同期電動機の全出力を\( \ P \ \mathrm {[W]} \ \)，同期速度を\( \ n_{\mathrm {s}} \ \mathrm {[{min}^{-1}]} \ \)とすると，トルク\( \ T \ \mathrm {[N\cdot m]} \ \)と\( \ P \ \)の関係は次式で表される。
\[
\begin{eqnarray}
P&=&3P_{\mathrm {o}} &=&2\pi \frac {n_{\mathrm {s}}}{60}T \\[ 5pt ] \end{eqnarray}
\] これから，\( \ T \ \)は次式のようになる。
\[
\begin{eqnarray}
T&=&\frac {60}{2\pi n_{\mathrm {s}}}\cdot 3P_{\mathrm {o}}=\frac {60}{2\pi n_{\mathrm {s}}}\cdot \frac {3VE}{x}\fbox {　 （イ） 　} \\[ 5pt ] \end{eqnarray}
\] 以上のことから，\( \ \displaystyle 0≦\delta ≦\frac {\pi }{2} \ \)の範囲において\( \ \delta \ \)が\( \ \fbox {　 （ウ） 　} \ \)なるに従って\( \ T \ \)は\( \ \fbox {　 （エ） 　} \ \)なり，理論上\( \ \displaystyle \frac {\pi }{2} \ \mathrm {[rad]} \ \)のとき\( \ \fbox {　 （オ） 　} \ \)となる。

上記の記述中の空白箇所(ア)，(イ)，(ウ)，(エ)及び(オ)に当てはまる組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。
\[
\begin{array}{cccccc}
& （ア） & （イ） & （ウ） & （エ） & （オ） \\
\hline
(1) & 負荷角 & \cos \delta & 大きく & 大きく & 最大値 \\
\hline
(2) & 力率角 & \cos \delta & 大きく & 小さく & 最小値 \\
\hline
(3) & 力率角 & \sin \delta & 小さく & 小さく & 最小値 \\
\hline
(4) & 負荷角 & \sin \delta & 大きく & 大きく & 最大値 \\
\hline
(5) & 負荷角 & \cos \delta & 小さく & 小さく & 最大値 \\
\hline
\end{array}
\]

【ワンポイント解説】

同期電動機の出力の式を暗記していれば解けてしまう問題です。電験の教科書でも最重要項目として必ずと言って良いほど扱われているので，確実に理解しておくようにしましょう。

1.同期電動機の出力
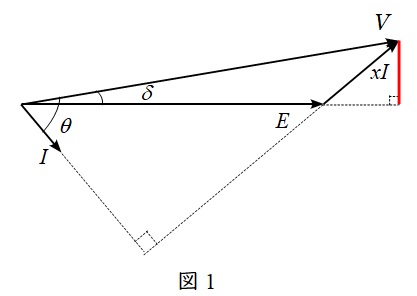
図1のように，\( \ 1 \ \)相分の誘導起電力\( \ E \ \mathrm {[V]} \ \)，電圧\( \ V \ \mathrm {[V]} \ \)，電流\( \ I \ \mathrm {[A]} \ \)，\( \ E \ \)と\( \ V \ \)の位相差（負荷角）を\( \ \delta \ \mathrm {[rad]} \ \)，\( \ V \ \)と\( \ I \ \)の位相差を\( \ \theta \ \mathrm {[rad]} \ \)とすると，\( \ 1 \ \)相分の出力\( \ P \ \)は，
\[
\begin{eqnarray}
P &=&EI\cos \left( \theta -\delta \right) \\[ 5pt ] \end{eqnarray}
\] で求められ，図1の赤線を求める式より，
\[
\begin{eqnarray}
xI\cos \left( \theta -\delta \right) &=&V\sin \delta \\[ 5pt ] I\cos \left( \theta -\delta \right) &=&\frac {V}{x}\sin \delta \\[ 5pt ] \end{eqnarray}
\] となるので，
\[
\begin{eqnarray}
P &=&EI\cos \left( \theta -\delta \right) \\[ 5pt ] &=&E\frac {V}{x}\sin \delta \\[ 5pt ] &=&\frac {VE}{x}\sin \delta \\[ 5pt ] \end{eqnarray}
\] と求められます。

　※この式は同期機出力の基本式として暗記しておきましょう。

【解答】

解答：(4)
(ア)
\( \ E \ \)と\( \ V \ \)の位相差\( \ \delta \ \)は負荷角と呼ばれます。

(イ)
ワンポイント解説「1.同期電動機の出力」の通り，\( \ 1 \ \)相分の出力\( \ P_{\mathrm {o}} \ \mathrm {[W]} \ \)は，
\[
\begin{eqnarray}
P_{\mathrm {o}} &=&\frac {VE}{x}\sin \delta \\[ 5pt ] \end{eqnarray}
\] で求められます。

(ウ)，(エ)，(オ)
題意より，
\[
\begin{eqnarray}
T&=&\frac {60}{2\pi n_{\mathrm {s}}}\cdot \frac {3VE}{x}\sin \delta \\[ 5pt ] \end{eqnarray}
\] で与えられ，\( \ \sin \ \)カーブの特徴により，\( \ \displaystyle 0≦\delta ≦\frac {\pi }{2} \ \)において，\( \ \delta \ \)が大きくなればなるほど\( \ \sin \delta \ \)が大きくなり，\( \ \sin \delta \ \)が最大となるのは\( \ \displaystyle \delta = \frac {\pi }{2} \ \)の時となります。

　※　(ウ)，(エ)の組合せは「大きく―大きく」もしくは「小さく―小さく」のどちらかとなり，確定はできません。