《機械》〈変圧器〉[H26:問8]単相変圧器の電圧変動に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は、単相変圧器の電圧変動に関する記述である。

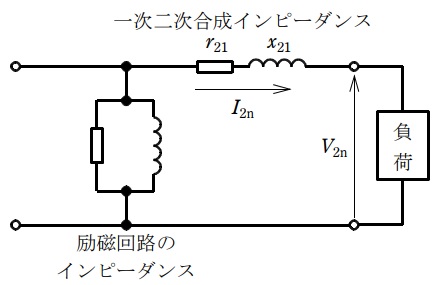
単相変圧器において，一次抵抗及び一次漏れリアクタンスが励磁回路のインピーダンスに比べて十分に小さいとして二次側に移した，二次側換算の簡易等価回路は図のようになる。\(r_{21}=1.0 \ \times \ 10^{-3}\Omega \)，\(x_{21}=3.0 \ \times \ 10^{-3}\Omega \)，定格二次電圧\(V_{\mathrm {2n}}= 100 \ \mathrm {V}\)，定格二次電流\(I_{\mathrm {2n}}= 1 \ \mathrm {kA}\)とする。

負荷の力率が遅れ\(80 \ ％\)のとき，百分率抵抗降下\(p\)，百分率リアクタンス降下\(q\)及び電圧変動率\(\varepsilon \)のそれぞれの値\([ ％ ]\)の組合せとして，最も近いものを次の(1)～(5)のうちから一つ選べ。なお，本問では簡単のため用いられる近似式を用いて解答すること。

\[
\begin{array}{cccc}
& 　p　 & 　q　 & 　\varepsilon　 \\
\hline
(1) & 3.0 & 1.0 & 3.0 \\
\hline
(2) & 3.0 & 1.0 & 2.4 \\
\hline
(3) & 1.0 & 3.0 & 3.1 \\
\hline
(4) & 1.0 & 2.6 & 3.0 \\
\hline
(5) & 1.0 & 3.0 & 2.6 \\
\hline
\end{array}
\]

【ワンポイント解説】

電圧変動率の公式を丸暗記しているだけでなく，考え方が分かっているかを問う問題となっています。半分以上の受験生は解けないと思う問題なので，問題不備により全員正解になったことは受験生としてはラッキーであったと思います。

1.電圧変動率の近似式
問題図において，左端の電圧を\(V_{20}\)とすると，電圧変動率\(\varepsilon \)は，
\[
\varepsilon =\frac {V_{20}-V_{\mathrm {2n}}}{V_{\mathrm {2n}}}\times 100 \ [％] \] で定義され，ベクトル図を描くと図1の通りとなるので，位相差\(\delta \)が十分に小さいとすると，
\[
\begin{eqnarray}
\varepsilon &=&\frac {V_{20}-V_{\mathrm {2n}}}{V_{\mathrm {2n}}}\times 100 \\[ 5pt ] &≒&\frac {r_{21}I_{\mathrm {2n}}\cos \theta +x_{21}I_{\mathrm {2n}}\sin \theta }{V_{\mathrm {2n}}}\times 100 \\[ 5pt ] &=&\frac {r_{21}I_{\mathrm {2n}}}{V_{\mathrm {2n}}}\cos \theta \times 100 +\frac {x_{21}I_{\mathrm {2n}}}{V_{\mathrm {2n}}}\sin \theta \times 100 \\[ 5pt ] &=&p\cos \theta +q\sin \theta \\[ 5pt ] \end{eqnarray}
\]

【関連する「電気の神髄」記事】

　　変圧器の電圧変動率

【解答】

解答：(5)
ワンポイント解説「1.電圧変動率の近似式」より，百分率抵抗降下\(p\)及び百分率リアクタンス降下\(q\)は，
\[
\begin{eqnarray}
p &=&\frac {r_{21}I_{\mathrm {2n}}}{V_{\mathrm {2n}}}\times 100 \\[ 5pt ] &=&\frac {1.0\times 10^{-3}\times 1.0\times 10^{3}}{100}\times 100 \\[ 5pt ] &=&1.0 \ [％] \end{eqnarray}
\] \[
\begin{eqnarray}
q &=&\frac {x_{21}I_{\mathrm {2n}}}{V_{\mathrm {2n}}}\times 100 \\[ 5pt ] &=&\frac {3.0\times 10^{-3}\times 1.0\times 10^{3}}{100}\times 100 \\[ 5pt ] &=&3.0 \ [％] \end{eqnarray}
\] と求められる。また，\(\sin \theta \)は，
\[
\begin{eqnarray}
\sin \theta &=&\sqrt {1-\cos ^{2} \theta } \\[ 5pt ] &=&\sqrt {1-0.8 ^{2}} \\[ 5pt ] &=&0.6
\end{eqnarray}
\] であるから，電圧変動率\(\varepsilon \)は，
\[
\begin{eqnarray}
\varepsilon &=&p\cos \theta +q\sin \theta \\[ 5pt ] &=&1.0\times 0.8+3.0\times 0.6 \\[ 5pt ] &=&2.6 \ [％] \end{eqnarray}
\] と求められる。