《機械》〈回転機〉[H28:問6]電動機のトルクに関する空欄穴埋問題

【問題】

【難易度】★★★☆☆（普通）

次の文章は，電源電圧一定(交流機の場合は多相交流巻線に印加する電源電圧の周波数も一定。)の条件下における各種電動機において，空回しの無負荷から，負荷の増大とともにトルクを発生する現象に関する記述である。

無負荷条件の直流分巻電動機では，回転速度に比例する\( \ \fbox {　 （ア） 　} \ \)と\( \ \fbox {　 （イ） 　} \ \)とがほぼ等しく，電機子電流がほぼ零となる。この状態から負荷が掛かって回転速度が低下すると，電機子電流が増大してトルクが発生する。
無負荷条件の誘導電動機では，周波数及び極数で決まる\( \ \fbox {　 （ウ） 　} \ \)と回転速度がほぼ等しく，\( \ \fbox {　 （エ） 　} \ \)がほぼ零となる。この状態から負荷が掛かって回転速度が低下すると，\( \ \fbox {　 （エ） 　} \ \)が増大してトルクが発生する。
無負荷条件の同期電動機では，界磁単独の磁束と電機子反作用を考慮した電機子磁束との位相差がほぼ零となる。この状態から負荷が掛かっても回転速度の低下はないが，上記両磁束の位相差，すなわち\( \ \fbox {　 （オ） 　} \ \)が増大してトルクが発生する。

上記の記述中の空白箇所(ア)，(イ)，(ウ)，(エ)及び(オ)に当てはまる組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。
\[
\begin{array}{cccccc}
& （ア） & （イ） & （ウ） & （エ） & （オ） \\
\hline
(1) & 逆起電力 & 電源電圧 & 同期速度 & 滑　り & 負荷角 \\
\hline
(2) & 誘導起電力 & 逆起電力 & 回転磁界 & 二次抵抗 & 負荷角 \\
\hline
(3) & 逆起電力 & 電源電圧 & 定格速度 & 二次抵抗 & 力率角 \\
\hline
(4) & 誘導起電力 & 逆起電力 & 同期速度 & 滑　り & 負荷角 \\
\hline
(5) & 逆起電力 & 電源電圧 & 回転磁界 & 滑　り & 力率角 \\
\hline
\end{array}
\]

【ワンポイント解説】

本問は各電動機の中身をきちんと理解しているかどうかが問われている問題です。本問は覚えていなくても解ける問題ではありますが，各電動機の等価回路は描けるようにしておきましょう。

1.直流分巻電動機の二次側等価回路
図1において，\( \ E \ \)を発電機では誘導起電力，電動機では逆起電力と言います。

\[
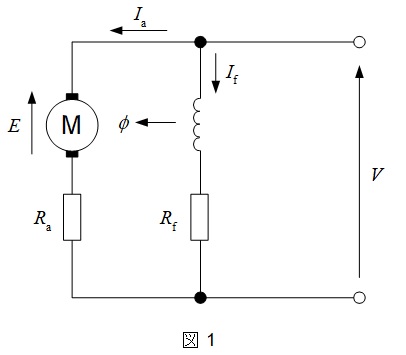
\begin{eqnarray}
&&V&:&電源電圧　&E&&:&逆起電力 \\[ 5pt ] &&I_{\mathrm {a}}&:&電機子電流　　　　　　&I_{\mathrm {f}}& &:&界磁電流 \\[ 5pt ] &&R_{\mathrm {a}}&:&電機子抵抗　&R_{\mathrm {f}}&&:&界磁抵抗 \\[ 5pt ] &&\phi&:&磁束
\end{eqnarray}
\]

2.三相誘導電動機の\( \ \mathrm {L} \ \)形等価回路
図2の通り，等価回路がやや複雑となります。回路右端の抵抗\( \ \displaystyle \frac {1-s}{s}r_{2}^{\prime } \ \)が出力に係る抵抗となります。

\[
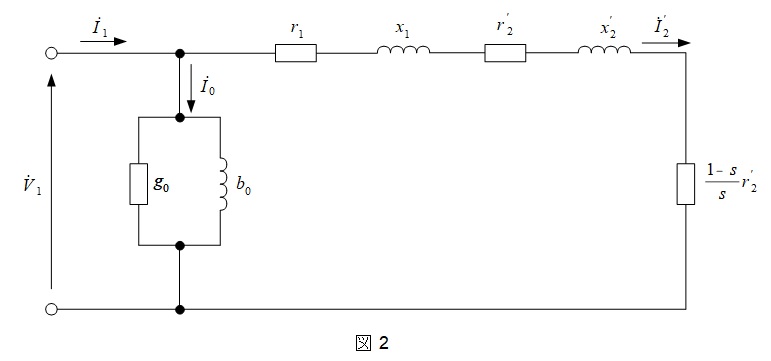
\begin{eqnarray}
&&\dot V_{1}&:&一次相電圧　&I_{1}&&:&一次電流 \\[ 5pt ] &&I_{2}^{\prime }&:&一次側に換算した二次電流　　　　　　　　　&I_{0}& &:&励磁電流 \\[ 5pt ] &&r_{1}&:&一次抵抗　&x_{1}&&:&一次リアクタンス \\[ 5pt ] &&r_{2}^{\prime }&:&一次側に換算した二次抵抗　&x_{2}^{\prime }&&:&一次側に換算した二次リアクタンス \\[ 5pt ] &&g_{0}&:&励磁コンダクタンス　&b_{0}&&:&励磁サセプタンス \\[ 5pt ] &&s&:&滑り
\end{eqnarray}
\]

3.同期電動機の等価回路及びベクトル図
同期電動機の\( \ 1 \ \)相分等価回路を図3に，ベクトル図を図4に示します。図4に示すように，電流が零であれば，\( \ \dot I \ \)に係る全てのベクトルが零となるので，\( \ \dot E \ \)と\( \ \dot V \ \)の位相差がなくなります。


\[
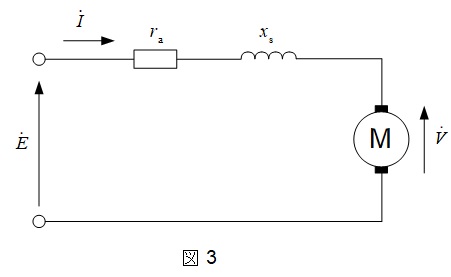
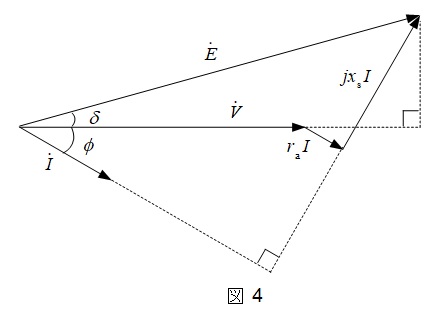
\begin{eqnarray}
&&\dot E&:&端子電圧　&\dot V&&:&誘導起電力 \\[ 5pt ] &&\dot I&:&電機子電流　&r_{\mathrm {a}}& &:&電機子巻線抵抗 \\[ 5pt ] &&x_{\mathrm {s}}&:&同期リアクタンス　　　　　　　&\delta &&:&負荷角 \\[ 5pt ] &&\phi &:&位相差
\end{eqnarray}
\]

【解答】

解答：(1)
(ア)，(イ)
図1の\( \ E \ \)を逆起電力，\( \ V \ \)を電源電圧と言います。誘導起電力は発電機の時の用語です。

(ウ)
周波数と極数で決まるのは同期速度です。周波数\( \ f \ \)，極数\( \ p \ \)とすると同期速度\( \ N_{\mathrm {s}} \ \)は，
\[
N_{\mathrm {s}}=\frac {120f}{p}
\] と求められます。

(エ)
滑り\( \ s \ \)は，
\[
s=\frac {N_{\mathrm {s}}-N}{N_{\mathrm {s}}}
\] となりますが，回転数\( \ N \ \)が同期速度\( \ N_{\mathrm {s}} \ \)と等しい時，滑り\( \ s=0 \ \)となります。

(オ)
図4のベクトル図の通り，同期電動機では負荷角が増大するとトルクが発生します。