Contents
【問題】
【難易度】★★★★☆(やや難しい)
図は,ある周波数伝達関数\( \ W\left( \mathrm {j}\omega \right) \ \)のボード線図の一部であり,折れ線近似でゲイン特性を示している。次の(a)及び(b)の問に答えよ。
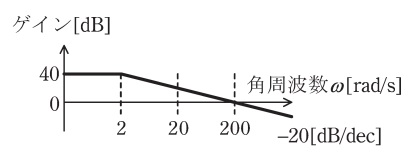
(a) 図のゲイン特性を示す周波数伝達関数として,最も適切なものを次の(1)~(5)のうちから一つ選べ。
\[
\begin{eqnarray}
&(1)& \ \displaystyle \frac {40}{1+\mathrm {j}\omega } \ &(2)& \ \displaystyle \frac {40}{1+\mathrm {j}0.005\omega } \ &(3)& \ \displaystyle \frac {100}{1+\mathrm {j}\omega } \ \\[ 5pt ]
&(4)& \ \displaystyle \frac {100}{1+\mathrm {j}0.005\omega } \ &(5)& \ \displaystyle \frac {100}{1+\mathrm {j}0.5\omega } \ && \\[ 5pt ]
\end{eqnarray}
\]
(b) 図のゲイン特性を示すブロック線図として,最も適切なものを次の(1)~(5)のうちから一つ選べ。ただし,入力を\( \ R\left( \mathrm {j}\omega \right) \ \),出力を\( \ C\left( \mathrm {j}\omega \right) \ \)として,図のゲイン特性を示しているものとする。
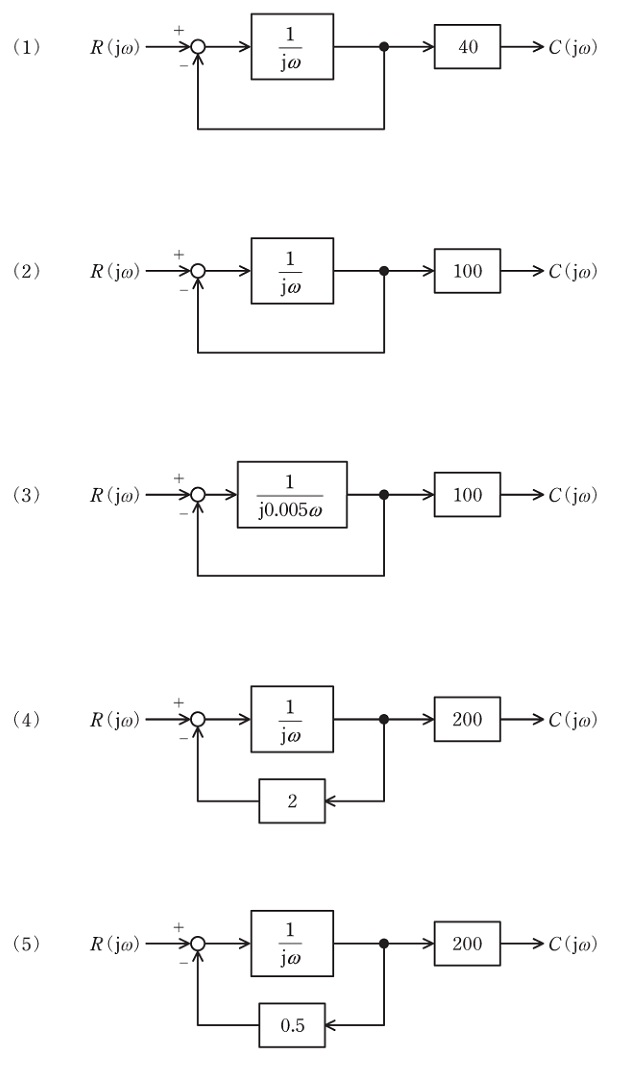
【ワンポイント解説】
ボード線図から周波数伝達関数を導出し,さらにブロック線図を導出する問題です。
ブロック線図が与えられて,その周波数伝達関数とボード線図を導出する問題が一般的ですが,逆から求める少しひねった問題と言えるかもしれません。
1.ブロック線図の等価変換
①直列
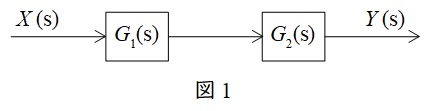
図1のような伝達関数\( \ G_{1}(s) \ \),\( \ G_{2}(s) \ \)が与えられているとき,全体の伝達関数\( \ G(s) \ \)は,
\[
\begin{eqnarray}
G(s)&=&\frac {Y(s)}{X(s)}=G_{1}(s)G_{2}(s) \\[ 5pt ]
\end{eqnarray}
\]
となります。
②並列
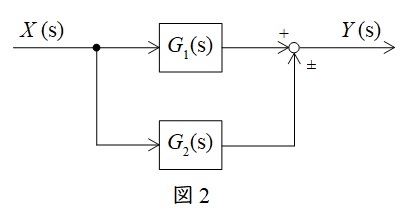
図2のような伝達関数\( \ G_{1}(s) \ \),\( \ G_{2}(s) \ \)が与えられているとき,全体の伝達関数\( \ G(s) \ \)は,
\[
\begin{eqnarray}
G(s)&=&\frac {Y(s)}{X(s)}=G_{1}(s)±G_{2}(s) \\[ 5pt ]
\end{eqnarray}
\]
となります。
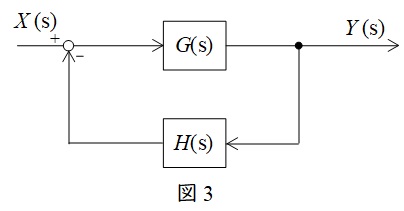
③フィードバック
図3のような\( \ G(s) \ \),\( \ H(s) \ \)が与えられているとき,全体の伝達関数\( \ W(s) \ \)は,
\[
\begin{eqnarray}
Y(s)&=&\left\{ X(s) -H(s)Y(s) \right\} G(s) \\[ 5pt ]
Y(s)&=&G(s)X(s) -G(s)H(s)Y(s) \\[ 5pt ]
Y(s)+G(s)H(s)Y(s) &=&G(s)X(s) \\[ 5pt ]
\left\{ 1+G(s)H(s)\right\} Y(s) &=&G(s)X(s) \\[ 5pt ]
\frac {Y(s)}{X(s)}&=&\frac {G(s)}{1+G(s)H(s)} \\[ 5pt ]
W(s)&=&\frac {G(s)}{1+G(s)H(s)} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.周波数伝達関数のゲイン
周波数伝達関数が\( \ \displaystyle W(\mathrm {j}\omega ) =\frac {K}{1+\mathrm {j}\omega T} \ \)で与えられる時,この周波数伝達関数の絶対値\( \ \left| W(\mathrm {j}\omega ) \right| \ \)は,
\[
\begin{eqnarray}
\left| W(\mathrm {j}\omega ) \right| &=&\left| \frac {K}{1+\mathrm {j}\omega T}\right| \\[ 5pt ]
&=&\frac {K}{\sqrt {1+\left( \omega T\right) ^{2}}} \\[ 5pt ]
&=&\frac {K}{\sqrt {1+\omega ^{2}T^{2}}} \\[ 5pt ]
\end{eqnarray}
\]
となり,この周波数伝達関数のゲイン\( \ g \ \)は
\[
\begin{eqnarray}
g&=&20\log _{10} \left| W(\mathrm {j}\omega )\right| \\[ 5pt ]
&=&20\log _{10} \frac {K}{\sqrt {1+\omega ^{2}T^{2}}} \\[ 5pt ]
&=&20\log _{10} K-20\log _{10} \sqrt {1+\omega ^{2}T^{2}} \\[ 5pt ]
&=&20\log _{10} K-10\log _{10} \left( 1+\omega ^{2}T^{2}\right) \ \mathrm {[dB]} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(a)解答:(5)
ボード線図において,角周波数\( \ \omega =0 \ \)のときゲイン\( \ g =40 \ \)であり,角周波数\( \ \omega =200 \ \)のときゲイン\( \ g =0 \ \)であるから,これを満たす周波数伝達関数を選択すればよい。
(1)について,
\[
\begin{eqnarray}
g&=&20\log _{10} \left| \frac {40}{1+\mathrm {j}\omega }\right| \\[ 5pt ]
&=&20\log _{10} \frac {40}{\sqrt {1+\omega ^{2}}} \\[ 5pt ]
\end{eqnarray}
\]
であるから,
\[
\begin{eqnarray}
g\left( 0 \right)&=&20\log _{10} \frac {40}{\sqrt {1+0 ^{2}}} \\[ 5pt ]
&=&20\log _{10}40≠40 \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
g\left( 200 \right)&=&20\log _{10} \frac {40}{\sqrt {1+200 ^{2}}} \\[ 5pt ]
&≒&20\log _{10} \frac {40}{200} \\[ 5pt ]
&=&-20\log _{10} 5≠0 \\[ 5pt ]
\end{eqnarray}
\]
となり不適切である。
(2)について,
\[
\begin{eqnarray}
g&=&20\log _{10} \left| \frac {40}{1+\mathrm {j}0.005\omega }\right| \\[ 5pt ]
&=&20\log _{10} \frac {40}{\sqrt {1+0.005^{2}\omega ^{2}}} \\[ 5pt ]
\end{eqnarray}
\]
であるから,
\[
\begin{eqnarray}
g\left( 0 \right)&=&20\log _{10} \frac {40}{\sqrt {1+0 ^{2}}} \\[ 5pt ]
&=&20\log _{10}40≠40 \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
g\left( 200 \right)&=&20\log _{10} \frac {40}{\sqrt {1+0.005^{2}\times 200 ^{2}}} \\[ 5pt ]
&=&20\log _{10} \frac {40}{\sqrt {2}} \\[ 5pt ]
&=&20\log _{10} 20\sqrt {2}≠0 \\[ 5pt ]
\end{eqnarray}
\]
となり不適切である。
(3)について,
\[
\begin{eqnarray}
g&=&20\log _{10} \left| \frac {100}{1+\mathrm {j}\omega }\right| \\[ 5pt ]
&=&20\log _{10} \frac {100}{\sqrt {1+\omega ^{2}}} \\[ 5pt ]
\end{eqnarray}
\]
であるから,
\[
\begin{eqnarray}
g\left( 0 \right)&=&20\log _{10} \frac {100}{\sqrt {1+0 ^{2}}} \\[ 5pt ]
&=&20\log _{10}100 \\[ 5pt ]
&=&20\times 2 \\[ 5pt ]
&=&40 \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
g\left( 200 \right)&=&20\log _{10} \frac {100}{\sqrt {1+200 ^{2}}} \\[ 5pt ]
&≒&20\log _{10} \frac {100}{200} \\[ 5pt ]
&=&20\log _{10} \frac {1}{2} \\[ 5pt ]
&=&-20\log _{10} 2≠0 \\[ 5pt ]
\end{eqnarray}
\]
となり不適切である。
(4)について,
\[
\begin{eqnarray}
g&=&20\log _{10} \left| \frac {100}{1+\mathrm {j}0.005\omega }\right| \\[ 5pt ]
&=&20\log _{10} \frac {100}{\sqrt {1+0.005^{2}\omega ^{2}}} \\[ 5pt ]
\end{eqnarray}
\]
であるから,
\[
\begin{eqnarray}
g\left( 0 \right)&=&20\log _{10} \frac {100}{\sqrt {1+0 ^{2}}} \\[ 5pt ]
&=&20\log _{10}100 \\[ 5pt ]
&=&20\times 2 \\[ 5pt ]
&=&40 \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
g\left( 200 \right)&=&20\log _{10} \frac {100}{\sqrt {1+0.005^{2}\times 200 ^{2}}} \\[ 5pt ]
&=&20\log _{10} \frac {100}{\sqrt {2}} \\[ 5pt ]
&=&20\log _{10} 50\sqrt {2}≠0 \\[ 5pt ]
\end{eqnarray}
\]
となり不適切である。
(5)について,
\[
\begin{eqnarray}
g&=&20\log _{10} \left| \frac {100}{1+\mathrm {j}0.5\omega }\right| \\[ 5pt ]
&=&20\log _{10} \frac {100}{\sqrt {1+0.5^{2}\omega ^{2}}} \\[ 5pt ]
\end{eqnarray}
\]
であるから,
\[
\begin{eqnarray}
g\left( 0 \right)&=&20\log _{10} \frac {100}{\sqrt {1+0 ^{2}}} \\[ 5pt ]
&=&20\log _{10}100 \\[ 5pt ]
&=&20\times 2 \\[ 5pt ]
&=&40 \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
g\left( 200 \right)&=&20\log _{10} \frac {100}{\sqrt {1+0.5^{2}\times 200 ^{2}}} \\[ 5pt ]
&=&20\log _{10} \frac {100}{\sqrt {10001}} \\[ 5pt ]
&≒&20\log _{10} \frac {100}{100} \\[ 5pt ]
&=&20\log _{10} 1 \\[ 5pt ]
&=&0 \\[ 5pt ]
\end{eqnarray}
\]
となり適切である。したがって,解答は(5)となる。
(b)解答:(4)
ワンポイント解説「1.ブロック線図の等価変換」に沿って,各図の周波数伝達関数\( \ \displaystyle W(\mathrm {j}\omega ) =\frac {C\left( \mathrm {j}\omega \right) }{R\left( \mathrm {j}\omega \right) } \ \)を求めると以下のようになる。
(1)
\[
\begin{eqnarray}
C\left( \mathrm {j}\omega \right) &=&\left \{ \left( \frac {\displaystyle \frac {1}{\mathrm {j}\omega }}{1+\displaystyle \frac {1}{\mathrm {j}\omega }\cdot 1} \right) \times 40 \right\} R\left( \mathrm {j}\omega \right) \\[ 5pt ]
&=&\left \{ \left( \frac {\displaystyle \frac {1}{\mathrm {j}\omega }}{\displaystyle \frac {1+\mathrm {j}\omega }{\mathrm {j}\omega }} \right) \times 40 \right\} R\left( \mathrm {j}\omega \right) \\[ 5pt ]
&=&\frac {40}{1+\mathrm {j}\omega } R\left( \mathrm {j}\omega \right) \\[ 5pt ]
∴ W(\mathrm {j}\omega ) &=&\frac {40}{1+\mathrm {j}\omega } \\[ 5pt ]
\end{eqnarray}
\]
と求められ,不適切である。
(2)
\[
\begin{eqnarray}
C\left( \mathrm {j}\omega \right) &=&\left \{ \left( \frac {\displaystyle \frac {1}{\mathrm {j}\omega }}{1+\displaystyle \frac {1}{\mathrm {j}\omega }\cdot 1} \right) \times 100 \right\} R\left( \mathrm {j}\omega \right) \\[ 5pt ]
&=&\left \{ \left( \frac {\displaystyle \frac {1}{\mathrm {j}\omega }}{\displaystyle \frac {1+\mathrm {j}\omega }{\mathrm {j}\omega }} \right) \times 100 \right\} R\left( \mathrm {j}\omega \right) \\[ 5pt ]
&=&\frac {100}{1+\mathrm {j}\omega } R\left( \mathrm {j}\omega \right) \\[ 5pt ]
∴ W(\mathrm {j}\omega ) &=&\frac {100}{1+\mathrm {j}\omega } \\[ 5pt ]
\end{eqnarray}
\]
と求められ,不適切である。
(3)
\[
\begin{eqnarray}
C\left( \mathrm {j}\omega \right) &=&\left \{ \left( \frac {\displaystyle \frac {1}{\mathrm {j}0.005\omega }}{1+\displaystyle \frac {1}{\mathrm {j}0.005\omega }\cdot 1} \right) \times 100 \right\} R\left( \mathrm {j}\omega \right) \\[ 5pt ]
&=&\left \{ \left( \frac {\displaystyle \frac {1}{\mathrm {j}0.005\omega }}{\displaystyle \frac {1+\mathrm {j}0.005\omega }{\mathrm {j}0.005\omega }} \right) \times 100 \right\} R\left( \mathrm {j}\omega \right) \\[ 5pt ]
&=&\frac {100}{1+\mathrm {j}0.005\omega } R\left( \mathrm {j}\omega \right) \\[ 5pt ]
∴ W(\mathrm {j}\omega ) &=&\frac {100}{1+\mathrm {j}0.005\omega } \\[ 5pt ]
\end{eqnarray}
\]
と求められ,不適切である。
(4)
\[
\begin{eqnarray}
C\left( \mathrm {j}\omega \right) &=&\left \{ \left( \frac {\displaystyle \frac {1}{\mathrm {j}\omega }}{1+\displaystyle \frac {1}{\mathrm {j}\omega }\cdot 2} \right) \times 200 \right\} R\left( \mathrm {j}\omega \right) \\[ 5pt ]
&=&\left \{ \left( \frac {\displaystyle \frac {1}{\mathrm {j}\omega }}{\displaystyle \frac {2+\mathrm {j}\omega }{\mathrm {j}\omega }} \right) \times 200 \right\} R\left( \mathrm {j}\omega \right) \\[ 5pt ]
&=&\frac {200}{2+\mathrm {j}\omega } R\left( \mathrm {j}\omega \right) \\[ 5pt ]
&=&\frac {100}{1+\mathrm {j}0.5\omega } R\left( \mathrm {j}\omega \right) \\[ 5pt ]
∴ W(\mathrm {j}\omega ) &=&\frac {100}{1+\mathrm {j}0.5\omega } \\[ 5pt ]
\end{eqnarray}
\]
と求められ,適切である。
(5)
\[
\begin{eqnarray}
C\left( \mathrm {j}\omega \right) &=&\left \{ \left( \frac {\displaystyle \frac {1}{\mathrm {j}\omega }}{1+\displaystyle \frac {1}{\mathrm {j}\omega }\cdot 0.5} \right) \times 200 \right\} R\left( \mathrm {j}\omega \right) \\[ 5pt ]
&=&\left \{ \left( \frac {\displaystyle \frac {1}{\mathrm {j}\omega }}{\displaystyle \frac {0.5+\mathrm {j}\omega }{\mathrm {j}\omega }} \right) \times 200 \right\} R\left( \mathrm {j}\omega \right) \\[ 5pt ]
&=&\frac {200}{0.5+\mathrm {j}\omega } R\left( \mathrm {j}\omega \right) \\[ 5pt ]
&=&\frac {400}{1+\mathrm {j}2\omega } R\left( \mathrm {j}\omega \right) \\[ 5pt ]
∴ W(\mathrm {j}\omega ) &=&\frac {400}{1+\mathrm {j}2\omega } \\[ 5pt ]
\end{eqnarray}
\]
と求められ,不適切である。
以上から,解答は(4)となる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは