《機械》〈電熱〉[R06下:問12]熱伝導によって壁を伝わる熱流に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

面積\( \ 25 \ \mathrm {m^{2}} \ \)，厚さ\( \ 10 \ \mathrm {cm} \ \)，熱伝導率\( \ 0.4 \ \mathrm {W / (m\cdot K) } \ \)の壁がある。この壁の内外面の温度差が\( \ 4 \ \mathrm {K} \ \)に保たれているとき，熱伝導によってこの壁を伝わる熱流\( \ \mathrm {[W]} \ \)の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 16 \ \)　　(2)　\( \ 40 \ \)　　(3)　\( \ 250 \ \)　　(4)　\( \ 400 \ \)　　(5)　\( \ 2 \ 500 \ \)

【ワンポイント解説】

熱伝導によって壁を伝わる熱流を求める問題です。
熱抵抗を求めてからオームの法則から熱流を求める問題で，電気回路で出題されたらほぼ全員が正答できる問題ですが，勉強が手薄になっている受験生も多い分野です。ぜひ合格のためにはこういう問題を正答するようにしましょう。
本問は平成10年問7からの再出題となります。

1.熱力学におけるオームの法則
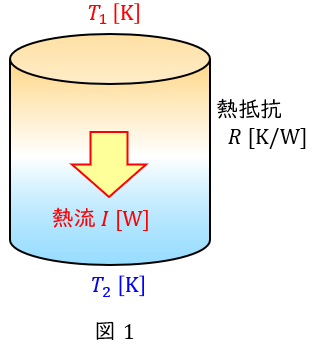
図1に示すように，ある温度差がある物体においては高温部から低温部に向かい熱が伝わり，それを熱流といいます。
物体の温度差を\( \ \theta =T_{1}-T_{2} \ \mathrm {[K]} \ \)，熱抵抗を\( \ R \ \mathrm {[K / W]} \ \)とすると，物体の熱流\( \ I \ \mathrm {[W]} \ \)は，
\[
\begin{eqnarray}
I &=& \frac {\theta }{R} \\[ 5pt ] \end{eqnarray}
\] となります。

2.物体の熱抵抗\( \ R \ \mathrm {[K / W]} \ \)
物体の熱伝導率が\( \ \lambda \ \mathrm {[W / (m\cdot K )]} \ \)，断面積が\( \ S \ \mathrm {[m^{2}]} \ \)，長さが\( \ l \ \mathrm {[m]} \ \)であるとき，物体の熱抵抗\( \ R \ \mathrm {[K / W]} \ \)は，
\[
\begin{eqnarray}
R &=& \frac {l}{\lambda S} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(4)
面積\( \ S=25 \ \mathrm {[m^{2}]} \ \)，厚さ\( \ l=0.1 \ \mathrm {m} \ \)，熱伝導率\( \ \lambda = 0.4 \ \mathrm {[W / (m\cdot K)] } \ \)の壁の熱抵抗\( \ R \ \mathrm {[K / W]} \ \)は，ワンポイント解説「2.物体の熱抵抗\( \ R \ \mathrm {[K / W]} \ \)」の通り，
\[
\begin{eqnarray}
R &=& \frac {l}{\lambda S} \\[ 5pt ] &=& \frac {0.1}{0.4\times 25} \\[ 5pt ] &=& 0.01 \ \mathrm {[K / W]} \\[ 5pt ] \end{eqnarray}
\] となるので，温度差\( \ \theta =4 \ \mathrm {[K]} \ \)のとき，壁を伝わる熱流\( \ I \ \mathrm {[W]} \ \)は，ワンポイント解説「1.熱力学におけるオームの法則」の通り，
\[
\begin{eqnarray}
I &=& \frac {\theta }{R} \\[ 5pt ] &=& \frac {4}{0.01} \\[ 5pt ] &=& 400 \ \mathrm {[W]} \\[ 5pt ] \end{eqnarray}
\] と求められる。