《機械》〈パワーエレクトロニクス〉[R07上:問16]可逆チョッパによる他励直流機の駆動に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

図のように他励直流機を直流チョッパで駆動する。電源電圧は\( \ E=200 \ \mathrm {V} \ \)で一定とし，直流機の電機子電圧を\( \ V \ \)とする。\( \ \mathrm {IGBT \ Q_{1}} \ \)及び\( \ \mathrm {Q_{2}} \ \)をオンオフ動作さ
せるときのスイッチング周波数は\( \ 500 \ \mathrm {Hz} \ \)であるとする。なお，本問では直流機の定常状態だけを扱うものとする。次の(a)及び(b)の問に答えよ。

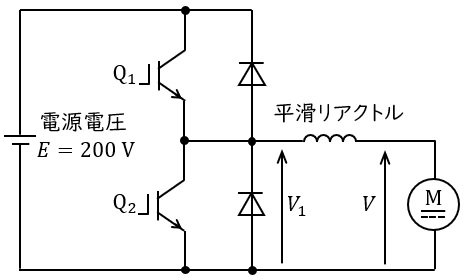
(a)　この直流機を電動機として駆動する場合，\( \ \mathrm {Q_{2}} \ \)をオフとし，\( \ \mathrm {Q_{1}} \ \)をオンオフ制御することで，\( \ V \ \)を調整することができる。電圧\( \ V_{1} \ \)の平均値が\( \ 150 \ \mathrm {V} \ \)のとき，\( \ 1 \ \)周期の中で\( \ \mathrm {Q_{1}} \ \)がオンになっている時間の値\( \ \mathrm {[ms]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 1.75 \ \)　　(2)　\( \ 1.50 \ \)　　(3)　\( \ 1.25 \ \)　　(4)　\( \ 1.00 \ \)　　(5)　\( \ 0.7 \ \)

(b)　\( \ \mathrm {Q_{1}} \ \)をオフして\( \ \mathrm {Q_{2}} \ \)をオンオフ制御することで，電機子電流の向きを(a)の場合と反対にし，直流機に発電動作（回生制動）をさせることができる。この制御において，スイッチングの\( \ 1 \ \)周期の間で\( \ \mathrm {Q_{2}} \ \)がオンになっている時間が\( \ 0.4 \ \mathrm {ms} \ \)のとき，この直流機の電機子電圧\( \ V \ \)の値\( \ \mathrm {[V]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 1 \ 000 \ \)　　(2)　\( \ 250 \ \)　　(3)　\( \ 200 \ \)　　(4)　\( \ 160 \ \)　　(5)　\( \ 40 \ \)

【ワンポイント解説】

可逆チョッパの動作や電圧を検討する問題です。
もちろん暗記が得意であれば出力電圧の式を丸暗記しても正答できますが，チョッパ回路で最も重要なのは動作原理です。ワンポイント解説の内容をよく理解して様々な問題に対応できるようにして下さい。
本問は平成26年問16からの再出題となります。

1.可逆チョッパ
降圧チョッパと昇圧チョッパを組み合わせたようなチョッパで，電源電圧と異なる負荷に電力を供給することと負荷の制動トルクを電源に回生することの両方が可能となります。
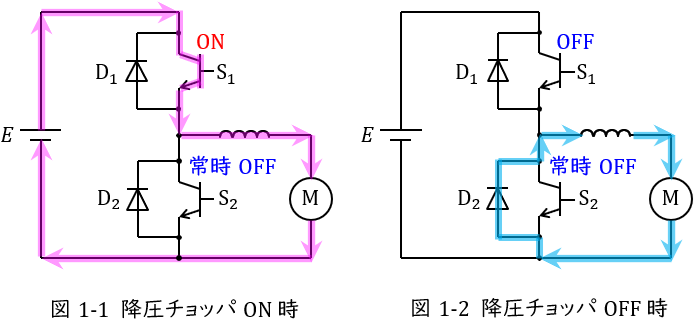
①降圧チョッパとして動作する時
図1-1及び図1-2のように動作します。
スイッチ\( \ \mathrm {S_{2}} \ \)は常時\( \ \mathrm {OFF} \ \)でスイッチ\( \ \mathrm {S_{1}} \ \)で\( \ \mathrm {ON－OFF} \ \)制御します。
\( \ \mathrm {S_{1}} \ \)が\( \ \mathrm {ON} \ \)の時，図1-1のように電源－\( \ \mathrm {S_{1}} \ \)－リアクトル－負荷－電源と導通し，リアクトルと負荷に電力が供給されます。
\( \ \mathrm {S_{1}} \ \)が\( \ \mathrm {OFF} \ \)の時，図1-2のようにリアクトル－負荷－\( \ \mathrm {D_{2}} \ \)－リアクトルと導通し，リアクトルに蓄えられているエネルギーが放出されます。
全体としてリアクトルに蓄えられるエネルギーと放出されるエネルギーの量が等しいので，負荷電圧を\( \ V \ \)とすると，
\[
\begin{eqnarray}
\left( E-V\right)IT_{\mathrm {on}} &=&VIT_{\mathrm {off}} \\[ 5pt ] \left( E-V\right)T_{\mathrm {on}} &=&VT_{\mathrm {off}} \\[ 5pt ] ET_{\mathrm {on}} &=&V\left( T_{\mathrm {on}}+T_{\mathrm {off}}\right) \\[ 5pt ] V &=&\frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}}E \\[ 5pt ] &=&\alpha E \\[ 5pt ] \end{eqnarray}
\] となり，\( \ \displaystyle \alpha =\frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}} \ \)を通流率といいます。\( \ \alpha ＜1 \ \)なので，\( \ E＞V \ \)となります。

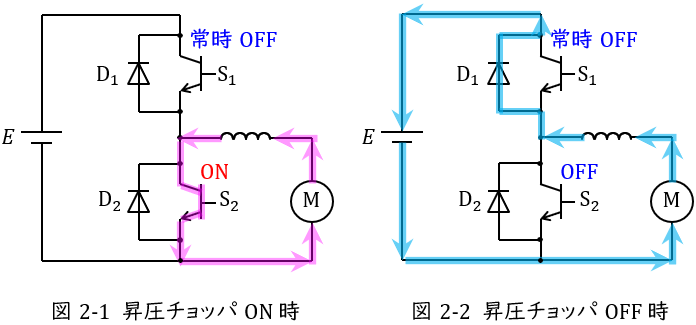
②昇圧チョッパとして動作する時
図2-1及び図2-2のように動作します。
スイッチ\( \ \mathrm {S_{1}} \ \)は常時\( \ \mathrm {OFF} \ \)でスイッチ\( \ \mathrm {S_{2}} \ \)で\( \ \mathrm {ON－OFF} \ \)制御します。
\( \ \mathrm {S_{2}} \ \)が\( \ \mathrm {ON} \ \)の時，図2-1のように負荷－リアクトル－\( \ \mathrm {S_{2}} \ \)－負荷と導通し，負荷からの回生エネルギーがリアクトルに蓄えられます。
\( \ \mathrm {S_{2}} \ \)が\( \ \mathrm {OFF} \ \)の時，図2-2のようにリアクトル－\( \ \mathrm {D_{1}} \ \)－電源－負荷－リアクトルと導通し，リアクトルに蓄えられているエネルギーが放出され，電源に回生されます。
全体としてリアクトルに蓄えられるエネルギーと放出されるエネルギーの量が等しいので，負荷電圧を\( \ V \ \)とすると，
\[
\begin{eqnarray}
VIT_{\mathrm {on}} &=&\left( E-V\right) IT_{\mathrm {off}} \\[ 5pt ] VT_{\mathrm {on}} &=&\left( E-V\right) T_{\mathrm {off}} \\[ 5pt ] V\left( T_{\mathrm {on}}+T_{\mathrm {off}}\right) &=&ET_{\mathrm {off}} \\[ 5pt ] E &=&\frac {T_{\mathrm {on}}+T_{\mathrm {off}}}{T_{\mathrm {off}}}V \\[ 5pt ] \end{eqnarray}
\] となります。上式を通流率\( \ \alpha \ \)を用いて表すと，
\[
\begin{eqnarray}
\alpha &=&\frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}} \\[ 5pt ] \left( T_{\mathrm {on}}+T_{\mathrm {off}}\right) \alpha &=&T_{\mathrm {on}} \\[ 5pt ] \alpha T_{\mathrm {off}}&=&\left( 1-\alpha \right) T_{\mathrm {on}} \\[ 5pt ] T_{\mathrm {on}}&=&\frac {\alpha }{1-\alpha }T_{\mathrm {off}} \\[ 5pt ] \end{eqnarray}
\] であるから，
\[
\begin{eqnarray}
E &=&\frac {T_{\mathrm {on}}+T_{\mathrm {off}}}{T_{\mathrm {off}}}V \\[ 5pt ] &=&\left( 1+\frac {T_{\mathrm {on}}}{T_{\mathrm {off}}}\right) V \\[ 5pt ] &=&\left( 1+\frac {\displaystyle \frac {\alpha }{1-\alpha }T_{\mathrm {off}}}{T_{\mathrm {off}}}\right) V \\[ 5pt ] &=&\left( 1+\frac {\alpha }{1-\alpha }\right) V \\[ 5pt ] &=&\frac {1}{1-\alpha } V \\[ 5pt ] \end{eqnarray}
\] となり，\( \ V＜E \ \)となります。

【解答】

(a)解答：(2)
ワンポイント解説「1.可逆チョッパ」の通り，\( \ \mathrm {Q_{2}} \ \)をオフとし，\( \ \mathrm {Q_{1}} \ \)をオンオフ制御することで，チョッパは降圧チョッパとして動作する。
スイッチング周波数\( \ f=500 \ \mathrm {[Hz]} \ \)なので，スイッチング周期\( \ T \ \mathrm {[ms]} \ \)は，
\[
\begin{eqnarray}
T &=&\frac {1}{f} \\[ 5pt ] &=&\frac {1}{500} \\[ 5pt ] &=&0.002 \ \mathrm {[s]} →　2 \ \mathrm {[ms]} \\[ 5pt ] \end{eqnarray}
\] となり，電圧\( \ V_{1} \ \)の平均値が\( \ 150 \ \mathrm {V} \ \)であるから，\( \ \mathrm {Q_{1}} \ \)がオンになっている時間\( \ T_{\mathrm {1on}} \ \mathrm {[ms]} \ \)は，ワンポイント解説「1.可逆チョッパ」の通り，
\[
\begin{eqnarray}
V_{1} &=&\frac {T_{\mathrm {1on}}}{T_{\mathrm {1on}}+T_{\mathrm {1off}}}E \\[ 5pt ] &=&\frac {T_{\mathrm {1on}}}{T}E \\[ 5pt ] T_{\mathrm {1on}}&=&\frac {V_{1}}{E}T \\[ 5pt ] &=&\frac {150}{200}\times 2 \\[ 5pt ] &=&1.5 \ \mathrm {[ms]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(4)
\( \ \mathrm {Q_{2}} \ \)がオンになっている時間\( \ T_{\mathrm {2on}}=0.4 \ \mathrm {[ms]} \ \)であるから，オフになっている時間は\( \ T_{\mathrm {2off}}=1.6 \ \mathrm {[ms]} \ \)である。したがって，直流機の電機子電圧\( \ V \ \mathrm {[V]} \ \)は，ワンポイント解説「1.可逆チョッパ」の通り，
\[
\begin{eqnarray}
E &=&\frac {T_{\mathrm {2on}}+T_{\mathrm {2off}}}{T_{\mathrm {2off}}}V \\[ 5pt ] V &=&\frac {T_{\mathrm {2off}}}{T_{\mathrm {2on}}+T_{\mathrm {2off}}}E \\[ 5pt ] &=&\frac {1.6}{0.4+1.6}\times 200 \\[ 5pt ] &=&160 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。