《理論》〈電気回路〉[H18:問7]電圧と電流が同相になるときの角周波数に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

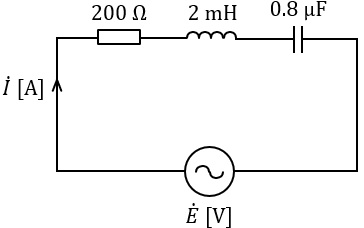
図のように，\( \ R=200 \ \mathrm {[\Omega ]} \ \)の抵抗，インダクタンス\( \ L=2 \ \mathrm {[mH]} \ \)のコイル，静電容量\( \ C=0.8 \ \mathrm {[\mu F]} \ \)のコンデンサを直列に接続した交流回路がある。この回路において，電源電圧\( \ \dot E \ \mathrm {[V]} \ \)と電流\( \ \dot I \ \mathrm {[A]} \ \)が同相であるとき，この電源の角周波数\( \ \omega \ \mathrm {[rad / s]} \ \)の値として，正しいのは次のうちどれか。

　(1)　\( \ 1.0\times 10^{3} \ \)　　(2)　\( \ 3.0\times 10^{3} \ \)　　(3)　\( \ 2.0\times 10^{4} \ \)
　(4)　\( \ 2.5\times 10^{4} \ \)　　(5)　\( \ 3.5\times 10^{4} \ \)

【ワンポイント解説】

\( \ RLC \ \)直列回路における電圧と電流が同相となるときの角周波数を求める問題です。
直列共振の公式にあてはめるだけの問題なので，電験の問題としては易しい問題になります。
根号を含む累乗の計算に少しコツを要するため，しっかりと解法を理解しておいて下さい。

1.直列回路の共振回路
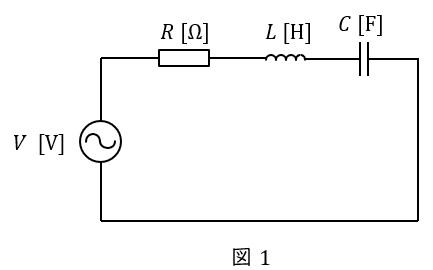
図1のような\( \ RLC \ \)直列回路があった場合の合成インピーダンス\( \ \dot Z \ \mathrm {[\Omega ]} \ \)は，角周波数を\( \ \omega \ \mathrm {[rad / s]} \ \)とすると，
\[
\begin{eqnarray}
\dot Z&=&R+\mathrm {j}\omega L +\frac {1}{\mathrm {j}\omega C} \\[ 5pt ] &=&R+\mathrm {j}\left( \omega L -\frac {1}{\omega C}\right) \\[ 5pt ] \end{eqnarray}
\] となり，インピーダンスが最も小さくなるためには，上式の虚数部が零である必要があります。よって，共振角周波数\( \ \omega _{\mathrm {c}} \ \mathrm {[rad / s]} \ \)は，
\[
\begin{eqnarray}
\omega_{\mathrm {c}} L -\frac {1}{\omega_{\mathrm {c}} C}&=&0 \\[ 5pt ] \omega_{\mathrm {c}} L &=&\frac {1}{\omega_{\mathrm {c}} C} \\[ 5pt ] \omega_{\mathrm {c}}^{2} &=&\frac {1}{LC} \\[ 5pt ] \omega_{\mathrm {c}} &=& \frac {1}{\sqrt {LC}} \\[ 5pt ] \end{eqnarray}
\] となります。また，共振周波数を\( \ f_{\mathrm {c}} \ \mathrm {[Hz]} \ \)とすると，\( \ \omega _{\mathrm {c}}=2\pi f_{\mathrm {c}} \ \)より，
\[
\begin{eqnarray}
f_{\mathrm {c}} &=& \frac {1}{2\pi \sqrt {LC}} \\[ 5pt ] \end{eqnarray}
\] となります。

2.並列回路の共振回路
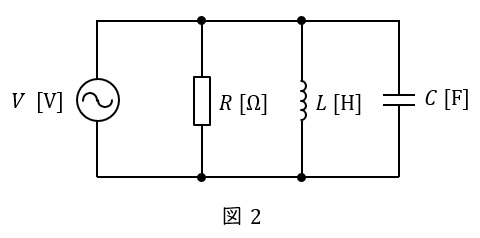
図2のような\( \ RLC \ \)並列回路があった場合の合成アドミタンス\( \ \dot Y \ \mathrm {[S]} \ \)は，角周波数を\( \ \omega \ \mathrm {[rad / s]} \ \)とすると，
\[
\begin{eqnarray}
\dot Y&=&\frac {1}{R}+\mathrm {j}\omega C +\frac {1}{\mathrm {j}\omega L} \\[ 5pt ] &=&\frac {1}{R}+\mathrm {j}\left( \omega C -\frac {1}{\omega L}\right)
\end{eqnarray}
\] となり，アドミタンスが最も小さくなるためには，上式の虚数部が零である必要があります。よって，共振角周波数\( \ \omega _{\mathrm {c}} \ \mathrm {[rad / s]} \ \)は，
\[
\begin{eqnarray}
\omega_{\mathrm {c}} C -\frac {1}{\omega_{\mathrm {c}} L}&=&0 \\[ 5pt ] \omega_{\mathrm {c}} C &=&\frac {1}{\omega_{\mathrm {c}} L} \\[ 5pt ] \omega_{\mathrm {c}}^{2} &=&\frac {1}{LC} \\[ 5pt ] \omega_{\mathrm {c}} &=& \frac {1}{\sqrt {LC}} \\[ 5pt ] \end{eqnarray}
\] となります。また，共振周波数を\( \ f_{\mathrm {c}} \ \mathrm {[Hz]} \ \)とすると，\( \ \omega _{\mathrm {c}}=2\pi f_{\mathrm {c}} \ \)より，
\[
\begin{eqnarray}
f_{\mathrm {c}} &=& \frac {1}{2\pi \sqrt {LC}} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(4)
電圧\( \ \dot E \ \mathrm {[V]} \ \)と電流\( \ \dot I \ \mathrm {[A]} \ \)が同相であるということは，直列共振の状態であるということなので，電源の角周波数\( \ \omega \ \mathrm {[rad / s]} \ \)は，ワンポイント解説「1.直列回路の共振回路」の通り，
\[
\begin{eqnarray}
\omega &=& \frac {1}{\sqrt {LC}} \\[ 5pt ] &=& \frac {1}{\sqrt {2\times 10^{-3}\times 0.8\times 10^{-6}}} \\[ 5pt ] &=& \frac {1}{\sqrt {1.6\times 10^{-9}}} \\[ 5pt ] &=& \frac {1}{\sqrt {16\times 10^{-10}}} \\[ 5pt ] &=& \frac {1}{4\times 10^{-5}} \\[ 5pt ] &=& 2.5\times 10^{4} \ \mathrm {[rad / s]} \\[ 5pt ] \end{eqnarray}
\] と求められる。