《理論》〈電気回路〉[H19:問6]ブリッジ回路の平衡条件と電流計を活用した抵抗値の導出に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

図のような直流回路において，スイッチ\( \ \mathrm {S} \ \)を閉じても，開いても電流計の指示値は，\( \ \displaystyle \frac {E}{4} \ \mathrm {[A]} \ \)一定である。このとき，抵抗\( \ R_{3} \ \mathrm {[\Omega ]} \ \)，\( \ R_{4} \ \mathrm {[\Omega ]} \ \)のうち小さい方の抵抗\( \ \mathrm {[\Omega ]} \ \)の値として，正しいのは次のうちどれか。

ただし，直流電圧源は\( \ E \ \mathrm {[V]} \ \)とし，電流計の内部抵抗は無視できるものとする。

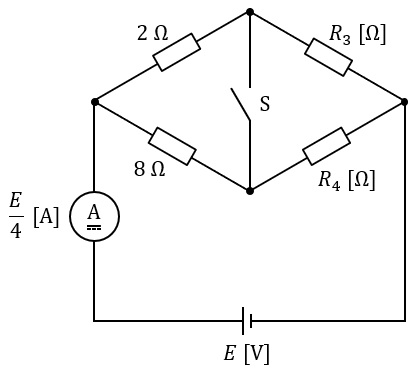
　(1)　\( \ 1 \ \)　　(2)　\( \ 2 \ \)　　(3)　\( \ 3 \ \)　　(4)　\( \ 4 \ \)　　(5)　\( \ 5 \ \)

【ワンポイント解説】

ブリッジ回路の平衡条件と電流計を活用した\( \ 2 \ \)つの未知の抵抗の抵抗値を導出する問題です。
ブリッジ回路の平衡条件は毎年のように出題される内容です。パターンも決まっていますので，必ず理解しておくようにして下さい。

1.合成抵抗
抵抗\( \ R_{1} \ \mathrm {[\Omega ]} \ \)と\( \ R_{2} \ \mathrm {[\Omega ]} \ \)が与えられている時，それぞれの合成抵抗\( \ R \ \mathrm {[\Omega ]} \ \)は以下の式で与えられます。

①直列
直列合成抵抗\( \ R \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
R&=&R_{1}+R_{2} \\[ 5pt ] \end{eqnarray}
\] となります。

②並列
並列合成抵抗\( \ R \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
\frac {1}{R}&=&\frac {1}{R_{1}}+\frac {1}{R_{2}} \\[ 5pt ] \end{eqnarray}
\] となり，整理すると，
\[
\begin{eqnarray}
R&=&\frac {R_{1}R_{2}}{R_{1}+R_{2}} \\[ 5pt ] \end{eqnarray}
\] となります。

2.直流ブリッジ回路の平衡条件
直流ブリッジ回路は抵抗の抵抗値を求める方法であり，ホイートストンブリッジと呼ばれます。
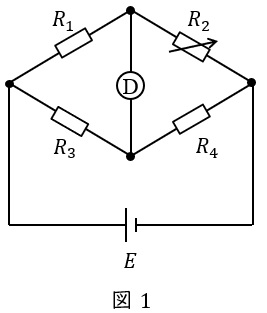
図1の回路において，検出器\( \ Ⓓ \ \)に電流が流れない条件を平衡条件と言い，
\[
\begin{eqnarray}
R_{1}R_{4} &=& R_{2}R_{3} \\[ 5pt ] \end{eqnarray}
\] の関係があります。したがって，３つの既知の抵抗があれば，残りの１つの抵抗値を求めることができます。

【解答】

解答：(3)
題意より，スイッチ\( \ \mathrm {S} \ \)を閉じても開いても電流計の指示値が変わらない，すなわち全体の抵抗値が変わらないので，ブリッジ回路の平衡条件が成立する。したがって，ワンポイント解説「2.直流ブリッジ回路の平衡条件」の通り，
\[
\begin{eqnarray}
2R_{4} &=& 8R_{3} \\[ 5pt ] R_{4} &=& 4R_{3} \\[ 5pt ] \end{eqnarray}
\] の関係が成立し，\( \ R_{3} \ \mathrm {[\Omega ]} \ \)の方が小さいことがわかる。また，電流計の指示値\( \ \displaystyle \frac {E}{4} \ \mathrm {[A]} \ \)より，回路全体の合成抵抗\( \ R \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
R &=& \frac {E}{\displaystyle \frac {E}{4}} \\[ 5pt ] &=& 4 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] であることから，スイッチ\( \ \mathrm {S} \ \)開放時の合成抵抗を求める式より，
\[
\begin{eqnarray}
R &=&\frac {\left( 2+R_{3}\right) \left( 8+R_{4}\right) }{\left( 2+R_{3}\right) +\left( 8+R_{4}\right) } \\[ 5pt ] 4&=&\frac {\left( 2+R_{3}\right) \left( 8+4R_{3}\right) }{\left( 2+R_{3}\right) +\left( 8+4R_{3}\right) } \\[ 5pt ] &=&\frac {4{R_{3}}^{2}+16R_{3}+16}{5R_{3}+10} \\[ 5pt ] 20R_{3}+40&=&4{R_{3}}^{2}+16R_{3}+16 \\[ 5pt ] 4{R_{3}}^{2}-4R_{3}-24&=&0 \\[ 5pt ] {R_{3}}^{2}-R_{3}-6&=&0 \\[ 5pt ] \left( R_{3}+2\right) \left( R_{3}-3\right) &=&0 \\[ 5pt ] R_{3} &=&3,\color {red}{-2（不適）} \\[ 5pt ] \end{eqnarray}
\] となり，\( \ R_{3}=3 \ \mathrm {[\Omega ]} \ \)と求められる。