《理論》〈電磁気〉[H28:問1]点電荷による等電位線を表す図に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

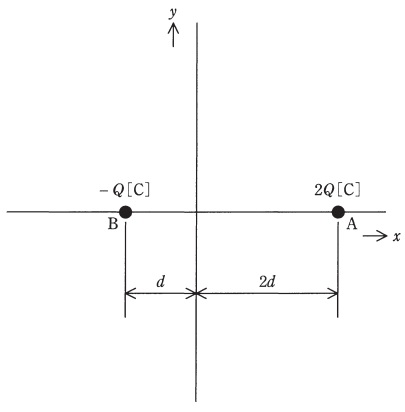
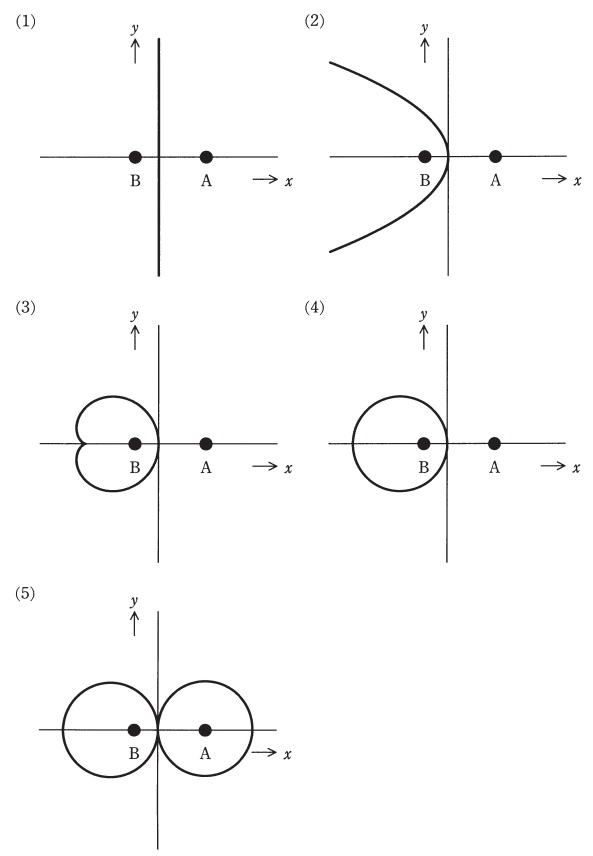
真空中において，図のように\( \ x \ \)軸上で距離\( \ 3d \ \mathrm {[m]} \ \)隔てた点\( \ \mathrm {A} \left( 2d，0\right) \ \)，点\( \ \mathrm {B} \left( -d，0\right) \ \)にそれぞれ\( \ 2Q \ \mathrm {[ C ] } \ \) ，\( \ -Q \ \mathrm {[ C ] } \ \)の点電荷が置かれている。\( \ xy \ \)平面上で電位が\( \ \mathrm {0 \ V} \ \)となる等電位線を表す図として，最も近いものを次の(1)～(5)のうちから一つ選べ。

【ワンポイント解説】

点電荷に関する問題で，参考書にも最初の方に出てくる内容ですが，電験となるとこういう問題はなかなか簡単にしてくれません。

1.静電界における電位
静電界中に点電荷\( \ Q \ \)がある時，\( \ Q \ \)から距離\( \ r \ \)離れた場所の電位\( \ V \ \)は，誘電率を\( \ \varepsilon \ \)とすると，
\[
\begin{eqnarray}
V&=&\frac {Q}{4\pi \varepsilon r} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(4)
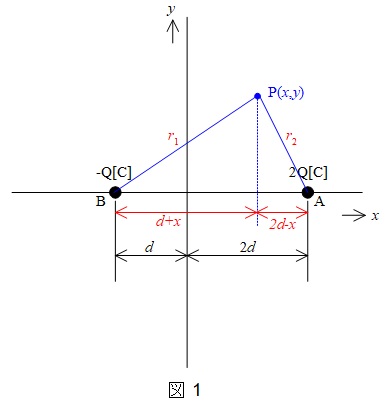
図1のように，任意の点\( \ \mathrm {P} \ \)における電位を求めると，
\[
\begin{eqnarray}
V&=&\frac {-Q}{4\pi \varepsilon r_{1}}+\frac {2Q}{4\pi \varepsilon r_{2}} \\[ 5pt ] \end{eqnarray}
\] となる。ここで電位が\( \ 0 \ \)となるためには，
\[
\begin{eqnarray}
\frac {-Q}{4\pi \varepsilon r_{1}}+\frac {2Q}{4\pi \varepsilon r_{2}}&=&0 \\[ 5pt ] \frac {2}{r_{2}}&=&\frac {1}{r_{1}} \\[ 5pt ] r_{2}&=&2r_{1} \\[ 5pt ] \end{eqnarray}
\] ここで，\( \ r_{1}= \sqrt {(d+x) ^{2}+y^{2}} \ \)，\( \ r_{2}=\sqrt { (2d-x) ^{2}+y^{2}} \ \)であるから，
\[
\begin{eqnarray}
r_{2}&=&2r_{1} \\[ 5pt ] \sqrt { (2d-x) ^{2}+y^{2}}&=&2\sqrt {(d+x) ^{2}+y^{2}} \\[ 5pt ] (2d-x) ^{2}+y^{2}&=&4\left\{ (d+x) ^{2}+y^{2}\right\} \\[ 5pt ] 4d^{2}-4dx+x^{2}+y^{2}&=&4d^{2}+8dx+4x^{2}+4y^{2} \\[ 5pt ] 3x^{2}+12dx+3y^{2}&=&0 \\[ 5pt ] x^{2}+4dx+y^{2}&=&0 \\[ 5pt ] \left( x+2d\right) ^{2}+y^{2}&=&\left( 2d\right) ^{2} \\[ 5pt ] \end{eqnarray}
\] よって，等電位線は\( \ (-2d，0) \ \)を中心とした半径\( \ 2d \ \)の線となる。