Contents
【問題】
【難易度】★★★★★(難しい)
図1のトランジスタによる小信号増幅回路について,次の(a)及び(b)の問に答えよ。
ただし,各抵抗は,\( \ R_{\mathrm {A}}=100 \ \mathrm {[k\Omega ]} \ \),\( \ R_{\mathrm {B}}=600 \ \mathrm {[k\Omega ]} \ \),\( \ R_{\mathrm {C}}=5 \ \mathrm {[k\Omega ]} \ \),\( \ R_{\mathrm {D}}=1 \ \mathrm {[k\Omega ]} \ \),\( \ R_{\mathrm {o}}=200 \ \mathrm {[k\Omega ]} \ \)である。\( \ \mathrm {C}_{\mathrm {1}} \ \),\( \ \mathrm {C}_{\mathrm {2}} \ \)は結合コンデンサで,\( \ \mathrm {C}_{\mathrm {3}} \ \)はバイパスコンデンサである。また,\( \ V_{\mathrm {CC}}=12 \ \mathrm {[V]} \ \)は直流電源電圧,\( \ V_{\mathrm {be}}=0.6 \ \mathrm {[V]} \ \)はベース-エミッタ間の直流電圧とし,\( \ v_{\mathrm {i}} \ \mathrm {[V]} \ \)は入力小信号電圧,\( \ v_{\mathrm {o}} \ \mathrm {[V]} \ \)は出力小信号電圧とする。
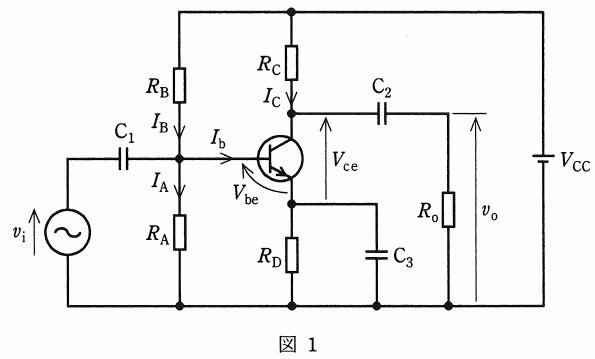
(a) 小信号増幅回路の直流ベース電流\( \ I_{\mathrm {b}} \ \mathrm {[A]} \ \)が抵抗\( \ R_{\mathrm {A}} \ \),\( \ R_{\mathrm {C}} \ \)の直流電流\( \ I_{\mathrm {A}} \ \mathrm {[A]} \ \)や\( \ I_{\mathrm {C}} \ \mathrm {[A]} \ \)に比べて十分に小さいものとしたとき,コレクタ-エミッタ間の直流電圧\( \ V_{\mathrm {ce}} \ \mathrm {[V]} \ \)の値として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 1.1 \ \) (2) \( \ 1.7 \ \) (3) \( \ 4.5 \ \) (4) \( \ 5.3 \ \) (5) \( \ 6.4 \ \)
(b) 小信号増幅回路の交流等価回路は,結合コンデンサ及びバイパスコンデンサのインピーダンスを無視することができる周波数において,一般に,図2の簡易等価回路で表される。
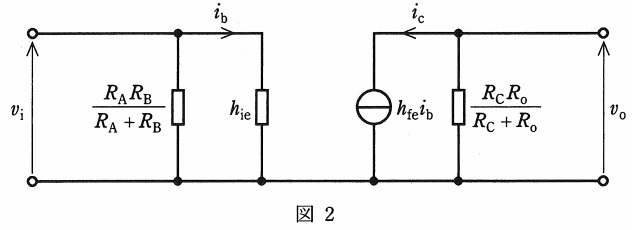
ここで,\( \ i_{\mathrm {b}} \ \mathrm {[A]} \ \)はベースの信号電流,\( \ i_{\mathrm {c}} \ \mathrm {[A]} \ \)はコレクタの信号電流で,この回路の電圧増幅度\( \ A_{\mathrm {v0}} \ \)は下式となる。
\[
\begin{eqnarray}
A_{\mathrm {v0}}&=&\left| \frac {v_{\mathrm {0}}}{v_{\mathrm {i}}}\right| =\frac {h_{\mathrm {fe}}}{h_{\mathrm {ie}}}\cdot \frac {R_{\mathrm {C}}R_{\mathrm {o}}}{R_{\mathrm {C}}+R_{\mathrm {o}}} ・・・・・・・・・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
また,コンデンサ\( \ \mathrm {C}_{\mathrm {1}} \ \)のインピーダンスの影響を考慮するための等価回路を図3に示す。
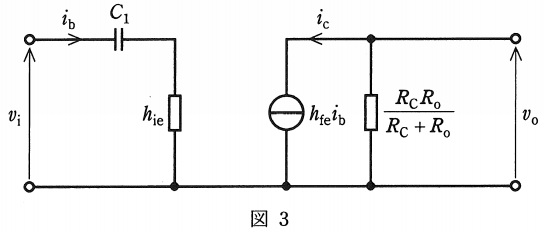
このとき,入力小信号電圧のある周波数において,図3を用いて得られた電圧増幅度が①式で示す電圧増幅度の\( \ \displaystyle \frac {1}{\sqrt {2}} \ \)となった。この周波数\( \ \mathrm {[Hz]} \ \)の大きさとして,最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし,エミッタ接地の小信号電流増幅率\( \ h_{\mathrm {fe}}=120 \ \),入力インピーダンス\( \ h_{\mathrm {ie}}=3\times 10^{3} \ \mathrm {[\Omega ]} \ \),コンデンサ\( \ \mathrm {C}_{\mathrm {1}} \ \)の静電容量\( \ C_{\mathrm {1}}=10 \ \mathrm {[\mu F]} \ \)とする。
(1) \( \ 1.2 \ \) (2) \( \ 1.6 \ \) (3) \( \ 2.1 \ \) (4) \( \ 5.3 \ \) (5) \( \ 7.9 \ \)
【ワンポイント解説】
トランジスタを用いた増幅回路に関する問題です。
\( \ 3 \ \)種としては計算量が多いため難易度は高めとしていますが,電子回路の基本を理解していれば特別難解な公式を使用することもなく(a)はかなりパターン化された問題,(b)は数学の計算問題,であるためいずれも十分に得点できる可能性があります。
【解答】
(a)解答:(4)
直流電圧分について,図1-1の閉回路について,分圧の法則を適用すると,
\[
\begin{eqnarray}
V_{\mathrm {b}}&=&\frac {R_{\mathrm {A}}}{R_{\mathrm {A}}+R_{\mathrm {B}}}V_{\mathrm {CC}} \\[ 5pt ]
&=&\frac {100\times 10^{3}}{100\times 10^{3}+600\times 10^{3}}\times 12 \\[ 5pt ]
&≒&1.714 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
となる。

題意より,ベース-エミッタ間電圧\( \ V_{\mathrm {be}}=0.6 \ \mathrm {[V]} \ \)であるから,エミッタ電圧\( \ V_{\mathrm {e}} \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {e}}&=&V_{\mathrm {b}}-V_{\mathrm {be}} \\[ 5pt ]
&=&1.714-0.6 \\[ 5pt ]
&≒&1.114 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,直流エミッタ電流\( \ I_{\mathrm {E}} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
I_{\mathrm {E}}&=&\frac {V_{\mathrm {e}}}{R_{\mathrm {D}}} \\[ 5pt ]
&=&\frac {1.114}{1\times 10^{3}} \\[ 5pt ]
&=&1.114\times 10^{-3} \ \mathrm {[A]} → 1.114 \ \mathrm {[mA]} \\[ 5pt ]
\end{eqnarray}
\]
となる。直流ベース電流\( \ I_{\mathrm {b}} \ \mathrm {[A]} \ \)は十分に小さいので\( \ I_{\mathrm {C}}≒I_{\mathrm {E}} \ \)となるから,コレクタ電圧\( \ V_{\mathrm {c}} \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {c}}&=&V_{\mathrm {CC}}-R_{\mathrm {C}}I_{\mathrm {C}} \\[ 5pt ]
&=&12-5\times 10^{3}\times 1.114\times 10^{-3} \\[ 5pt ]
&=&6.430 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
となる。以上から,コレクタ-エミッタ間直流電圧\( \ V_{\mathrm {ce}} \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {ce}}&=&V_{\mathrm {c}}-V_{\mathrm {e}} \\[ 5pt ]
&=&6.430-1.114 \\[ 5pt ]
&=&5.316 \ \mathrm {[V]} → 5.3 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。

(b)解答:(4)
図3において,
\[
\begin{eqnarray}
v_{\mathrm {i}}&=&\left( h_{\mathrm {ie}}+\frac {1}{\mathrm {j}2\pi f C_{\mathrm {1}}}\right) i_{\mathrm {b}} \\[ 5pt ]
v_{\mathrm {o}}&=&\frac {R_{\mathrm {C}}R_{\mathrm {o}}}{R_{\mathrm {C}}+R_{\mathrm {o}}} \left( -h_{\mathrm {fe}} i_{\mathrm {b}}\right) \\[ 5pt ]
\end{eqnarray}
\]
であるから,電圧増幅度\( \ A_{\mathrm {v}} \ \)は,
\[
\begin{eqnarray}
A_{\mathrm {v}}&=&\left| \frac {v_{\mathrm {0}}}{v_{\mathrm {i}}}\right| \\[ 5pt ]
&=&\frac {\displaystyle \frac {R_{\mathrm {C}}R_{\mathrm {o}}}{R_{\mathrm {C}}+R_{\mathrm {o}}} \cdot h_{\mathrm {fe}} i_{\mathrm {b}} }{\displaystyle \sqrt{ h_{\mathrm {ie}}^{2}+\frac {1}{\left( 2\pi f C_{\mathrm {1}} \right) ^{2}}} i_{\mathrm {b}}} \\[ 5pt ]
&=&\frac {\displaystyle \frac {R_{\mathrm {C}}R_{\mathrm {o}}}{R_{\mathrm {C}}+R_{\mathrm {o}}} }{\displaystyle \sqrt{ h_{\mathrm {ie}}^{2}+\frac {1}{\left( 2\pi f C_{\mathrm {1}} \right) ^{2}}} }h_{\mathrm {fe}} \\[ 5pt ]
\end{eqnarray}
\]
となる。この電圧増幅度\( \ A_{\mathrm {v}} \ \)が①式の\( \ A_{\mathrm {v0}} \ \)の\( \ \displaystyle \frac {1}{\sqrt {2}} \ \)倍の大きさとなるので,
\[
\begin{eqnarray}
A_{\mathrm {v}}&=&\frac {1}{\sqrt {2}}A_{\mathrm {v0}} \\[ 5pt ]
\frac {\displaystyle \frac {R_{\mathrm {C}}R_{\mathrm {o}}}{R_{\mathrm {C}}+R_{\mathrm {o}}} }{\displaystyle \sqrt{ h_{\mathrm {ie}}^{2}+\frac {1}{\left( 2\pi f C_{\mathrm {1}} \right) ^{2}}} }h_{\mathrm {fe}} &=& \frac {1}{\sqrt {2}} \cdot \frac {h_{\mathrm {fe}}}{h_{\mathrm {ie}}}\cdot \frac {R_{\mathrm {C}}R_{\mathrm {o}}}{R_{\mathrm {C}}+R_{\mathrm {o}}} \\[ 5pt ]
\frac {1}{\displaystyle \sqrt{ h_{\mathrm {ie}}^{2}+\frac {1}{\left( 2\pi f C_{\mathrm {1}} \right) ^{2}}}} &=& \frac {1}{\sqrt {2}h_{\mathrm {ie}}} \\[ 5pt ]
\sqrt {2}h_{\mathrm {ie}} &=& \sqrt{ h_{\mathrm {ie}}^{2}+\frac {1}{\left( 2\pi f C_{\mathrm {1}} \right) ^{2}}} \\[ 5pt ]
2h_{\mathrm {ie}}^{2} &=& h_{\mathrm {ie}}^{2}+\frac {1}{\left( 2\pi f C_{\mathrm {1}} \right) ^{2}} \\[ 5pt ]
h_{\mathrm {ie}}^{2} &=& \frac {1}{\left( 2\pi f C_{\mathrm {1}} \right) ^{2}} \\[ 5pt ]
h_{\mathrm {ie}} &=& \frac {1}{ 2\pi f C_{\mathrm {1}} } \\[ 5pt ]
f &=& \frac {1}{ 2\pi C_{\mathrm {1}}h_{\mathrm {ie}} } \\[ 5pt ]
\end{eqnarray}
\]
と整理されるので,各値を代入すると,
\[
\begin{eqnarray}
f &=& \frac {1}{ 2\pi \times 10\times 10^{-6} \times 3\times 10^{3} } \\[ 5pt ]
&≒& 5.31 \ \mathrm {[Hz]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは