《理論》〈電気回路〉[H19:問8]電源の周波数を変化させたときの力率変化に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

図のように，\( \ 8 \ \mathrm {[\Omega ]} \ \)の抵抗と静電容量\( \ C \ \mathrm {[F]} \ \)のコンダンサを直列に接続した交流回路がある。この回路において，電源\( \ E \ \mathrm {[V]} \ \)の周波数を\( \ 50 \ \mathrm {[Hz]} \ \)にしたときの回路の力率は，\( \ 80 \ \mathrm {[％]} \ \)になる。電源\( \ E \ \mathrm {[V]} \ \)の周波数を\( \ 25 \ \mathrm {[Hz]} \ \)にしたときの回路の力率\( \ \mathrm {[％]} \ \)の値として，最も近いのは次のうちどれか。

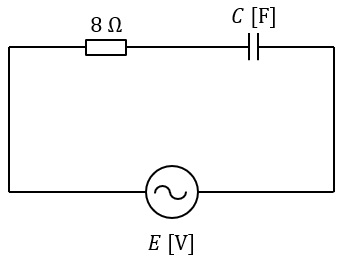
　(1)　\( \ 40 \ \)　　(2)　\( \ 42 \ \)　　(3)　\( \ 56 \ \)　　(4)　\( \ 60 \ \)　　(5)　\( \ 83 \ \)

【ワンポイント解説】

\( \ RC \ \)回路において，電源周波数を変化させたときの力率変化を検討する問題です。
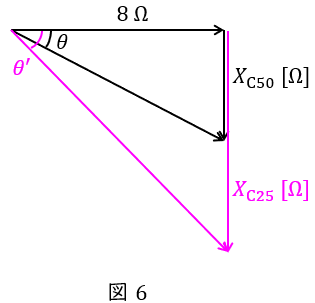
まずは図6のようなベクトル図を描き，力率がどれくらい大きくなるか小さくなるかを予想してから解いていくと選択肢も絞れ，間違いは少なくなるかと思います。細かな計算も大事ですが，概要を掴むことも重要です。

1.抵抗，コイル，コンデンサの電圧\( \ V \ \mathrm {[V]} \ \)と電流\( \ I \ \mathrm {[A]} \ \)の関係
抵抗\( \ R \ \mathrm {[\Omega ]} \ \)，コイル\( \ L \ \mathrm {[H]} \ \)，コンデンサ\( \ C \ \mathrm {[F]} \ \)があり，電源の角周波数\( \ \omega \ \mathrm {[rad / s]} \ \)及び周波数\( \ f \ \mathrm {[Hz]} \ \)が与えられているとき，それぞれのインピーダンスは，
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {R}}&=&R&& \\[ 5pt ] {\dot Z}_{\mathrm {L}}&=&\mathrm {j}\omega L&=&\mathrm {j}2\pi f L \\[ 5pt ] {\dot Z}_{\mathrm {C}}&=&\frac {1}{\mathrm {j}\omega C}&=&\frac {1}{\mathrm {j}2\pi f C} \\[ 5pt ] \end{eqnarray}
\] で求められ，それぞれの電圧と電流の関係は，
\[
\begin{eqnarray}
{\dot V}_{\mathrm {R}}&=&R\dot I \\[ 5pt ] {\dot V}_{\mathrm {L}}&=&\mathrm {j}\omega L \dot I \\[ 5pt ] {\dot V}_{\mathrm {C}}&=&\frac {\dot I }{\mathrm {j}\omega C} \\[ 5pt ] \end{eqnarray}
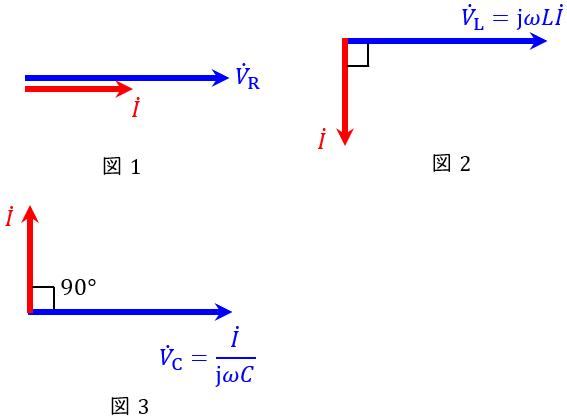
\] となります。この関係をベクトル図に表すと，図1～図3となります。

2.有効電力\( \ P \ \mathrm {[W]} \ \)と無効電力\( \ Q \ \mathrm {[var]} \ \)
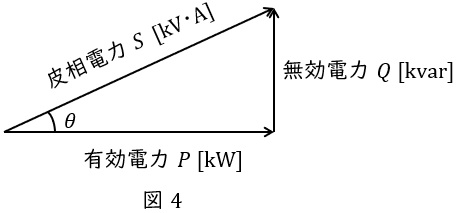
抵抗で消費される電力を有効電力\( \ P \ \mathrm {[W]} \ \)，リアクタンスで消費もしくは供給される電力を無効電力\( \ Q \ \mathrm {[var]} \ \)と呼び，図4のようにベクトル図を描きます。さらに，有効電力\( \ P \ \mathrm {[W]} \ \)と無効電力\( \ Q \ \mathrm {[var]} \ \)のベクトル和は皮相電力\( \ S \ \mathrm {[V\cdot A]} \ \)と呼ばれ，
\[
\begin{eqnarray}
S&=&\sqrt {P^{2}+Q^{2}} \\[ 5pt ] \end{eqnarray}
\] の関係があります。図4において，力率は\( \ \cos \theta \ \)で定義され，
\[
\begin{eqnarray}
\cos \theta &=&\frac {P}{S} \\[ 5pt ] \end{eqnarray}
\] となります。

また，線路に電流\( \ I \ \mathrm {[A]} \ \)が流れているとき，皮相電力\( \ S \ \mathrm {[V\cdot A]} \ \)，有効電力\( \ P \ \mathrm {[W]} \ \)，無効電力\( \ Q \ \mathrm {[var]} \ \)は，インピーダンスを\( \ Z \ \mathrm {[\Omega ]} \ \)，抵抗を\( \ R \ \mathrm {[\Omega ]} \ \)，リアクタンスを\( \ X \ \mathrm {[\Omega ]} \ \)とすると，
\[
\begin{eqnarray}
S &=&ZI^{2} \\[ 5pt ] P &=&RI^{2} \\[ 5pt ] Q &=&XI^{2} \\[ 5pt ] \end{eqnarray}
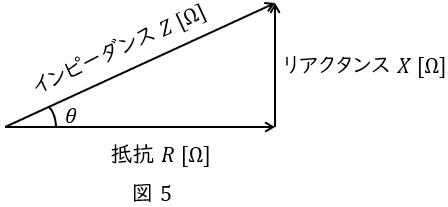
\] となるため，\( \ Z \ \mathrm {[\Omega ]} \ \)，\( \ R \ \mathrm {[\Omega ]} \ \)，\( \ X \ \mathrm {[\Omega ]} \ \)に関しても電力と同様な図5のような関係を描くことができます。

【解答】

解答：(3)
ワンポイント解説「1.抵抗，コイル，コンデンサの電圧\( \ V \ \mathrm {[V]} \ \)と電流\( \ I \ \mathrm {[A]} \ \)の関係」の通り，コンデンサのリアクタンスは周波数に反比例するので，周波数が\( \ 25 \ \mathrm {[Hz]} \ \)になるとリアクタンスは\( \ 2 \ \)倍となる。したがって，ベクトル図は図6のようになる。

周波数\( \ 50 \ \mathrm {[Hz]} \ \)のときの力率が\( \ \cos \theta =0.8 \ \)なので，\( \ \sin \theta \ \)は，
\[
\begin{eqnarray}
\sin \theta &=&\sqrt {1-\cos ^{2}\theta } \\[ 5pt ] &=&\sqrt {1-0.8 ^{2} } \\[ 5pt ] &=&0.6 \\[ 5pt ] \end{eqnarray}
\] であり，このときのリアクタンス\( \ X_{50} \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
X_{50}&=&8\tan \theta \\[ 5pt ] &=&8\cdot \frac {\sin \theta }{\cos \theta } \\[ 5pt ] &=&8\times \frac {0.6}{0.8} \\[ 5pt ] &=&6 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となる。よって，\( \ 25 \ \mathrm {[Hz]} \ \)のときのリアクタンス\( \ X_{25} \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
X_{25}&=&2X_{50} \\[ 5pt ] &=&2\times 6 \\[ 5pt ] &=&12 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となるので，このときの力率\( \ \cos \theta ^{\prime } \ \)は，
\[
\begin{eqnarray}
\cos \theta ^{\prime }&=&\frac {8}{\sqrt {8^{2}+{X_{25}}^{2}}} \\[ 5pt ] &=&\frac {8}{\sqrt {8^{2}+12^{2}}} \\[ 5pt ] &≒&0.554 \ 7　→　55 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] と求められる。