《理論》〈電磁気〉[H20:問4]環状鉄心に巻くコイルの自己インダクタンスと巻数の関係に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

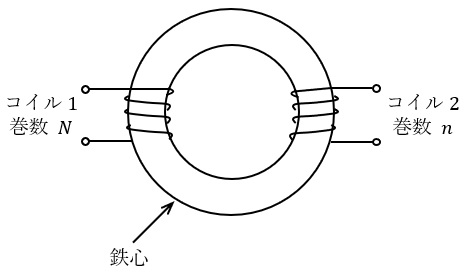
図のように，環状鉄心に二つのコイルが巻かれている。コイル\( \ 1 \ \)の巻数は\( \ N \ \)であり，その自己インダクタンスは\( \ L \ \mathrm {[H]} \ \)である。コイル\( \ 2 \ \)の巻数は\( \ n \ \)であり，その自己インダクタンスは\( \ 4L \ \mathrm {[H]} \ \)である。巻数\( \ n \ \)の値を表す式として，正しいのは次のうちどれか。

ただし，鉄心は等断面，等質であり，コイル及び鉄心の漏れ磁束はなく，また，鉄心の磁気飽和もないものとする。

　(1)　\( \ \displaystyle \frac {N}{4} \ \)　　(2)　\( \ \displaystyle \frac {N}{2} \ \)　　(3)　\( \ 2N \ \)　　(4)　\( \ 4N \ \)　　(5)　\( \ 16N \ \)

【ワンポイント解説】

環状鉄心に巻かれたコイルの自己インダクタンスから巻数の関係を求める問題です。
模範解答では以下に示す公式から導出していますが，知識として自己インダクタンス\( \ L \ \mathrm {[H]} \ \)が巻数\( \ N \ \)の\( \ 2 \ \)乗に比例することは覚えておいても良いかと思います。

1.ファラデーの電磁誘導の法則と自己インダクタンス\( \ L \ \)
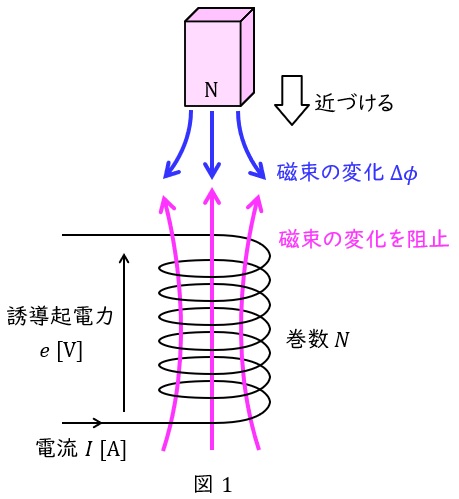
図1に示すように，巻数\( \ N \ \)のコイルを貫通する磁束\( \ \phi \ \mathrm {[Wb]} \ \)があるとき，ファラデーの電磁誘導の法則より，コイルに発生する誘導起電力\( \ e \ \mathrm {[V]} \ \)は，磁束の時間変化\( \ \displaystyle \frac {\Delta \phi }{\Delta t} \ \)に比例し，
\[
\begin{eqnarray}
e&=&−N\frac {\Delta \phi }{\Delta t} \\[ 5pt ] \end{eqnarray}
\] で求められます。これをファラデーの電磁誘導の法則といいます。一方，電流変化\( \ \Delta I \ \mathrm {[A]} \ \)を考える場合，
\[
\begin{eqnarray}
e&=&−L\frac {\Delta I }{\Delta t} \\[ 5pt ] \end{eqnarray}
\] という関係も成り立ち，\( \ L \ \mathrm {[H]}\ \)を自己インダクタンスと言います。これらの関係から，
\[
\begin{eqnarray}
−N\frac {\Delta \phi }{\Delta t}&=&−L\frac {\Delta I }{\Delta t} \\[ 5pt ] N\phi &=&LI \\[ 5pt ] \end{eqnarray}
\] の関係があります。

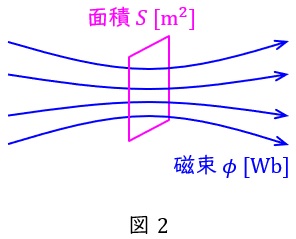
2.鎖交磁束数\( \ \phi \ \)と磁束密度\( \ B \ \)の関係
図2に示すように，面積\( \ S \ \mathrm {[m^{2}]} \ \)のコイルを磁束\( \ \phi \ \mathrm {[Wb]} \ \)が通過しているとき，コイル内の磁束密度\( \ B \ \mathrm {[T]} \ \)は，
\[
\begin{eqnarray}
B&=&\frac {\phi }{S} \\[ 5pt ] \end{eqnarray}
\] となります。

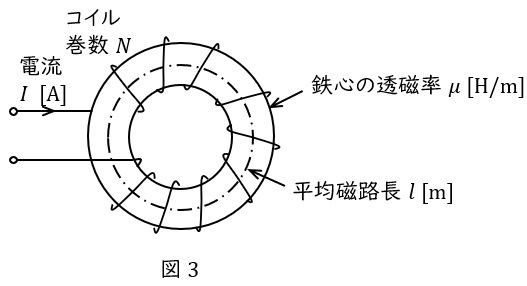
3.環状ソレノイド中の磁束密度
中心長さ\( \ l \ \mathrm {[ m ]} \ \)の環状鉄心に巻き数\( \ N \ \)のコイルが巻かれ，そこに電流\( \ I \ \mathrm {[ A ]} \ \)が流れている時，鉄心内の磁界の強さ\( \ H \ \mathrm {[ A / m ]} \ \)は，アンペールの周回積分の法則より，
\[
\begin{eqnarray}
NI&=&Hl \\[ 5pt ] H&=&\frac {NI}{l} \\[ 5pt ] \end{eqnarray}
\] となります。また，鉄心内の磁束密度\( \ B \ \mathrm {[ T ]} \ \)は，鉄心内の透磁率\( \ \mu \ \mathrm {[ H / m ]} \ \)とすると，
\[
\begin{eqnarray}
B&=&\mu H \\[ 5pt ] &=&\frac {\mu NI}{l} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(3)
ワンポイント解説「1.ファラデーの電磁誘導の法則と自己インダクタンス\( \ L \ \)」より，
\[
\begin{eqnarray}
LI&=&N\phi \\[ 5pt ] L&=&\frac {N\phi }{I} \\[ 5pt ] \end{eqnarray}
\] の関係があり，ワンポイント解説「2.鎖交磁束数\( \ \phi \ \)と磁束密度\( \ B \ \)の関係」及び「3.環状ソレノイド中の磁束密度」の通り，
\[
\begin{eqnarray}
\phi &=&BS \\[ 5pt ] &=&\mu HS \\[ 5pt ] &=&\frac {\mu NIS}{l} \\[ 5pt ] \end{eqnarray}
\] の関係があるため，
\[
\begin{eqnarray}
L&=&\frac {N\phi }{I} \\[ 5pt ] &=&\frac {N}{I}\times \frac {\mu NIS}{l} \\[ 5pt ] &=&\frac {\mu N^{2}S}{l} \\[ 5pt ] \end{eqnarray}
\] となり，自己インダクタンス\( \ L \ \)は巻数\( \ N \ \)の\( \ 2 \ \)乗に比例する。したがって，コイル\( \ 1 \ \)及び\( \ 2 \ \)の巻数の関係は，
\[
\begin{eqnarray}
\frac {4L}{L}&=&\left( \frac {n}{N}\right) ^{2} \\[ 5pt ] \left( \frac {n}{N}\right) ^{2} &=&4 \\[ 5pt ] \frac {n}{N} &=&2 \\[ 5pt ] n&=&2N \\[ 5pt ] \end{eqnarray}
\] と求められる。