《理論》〈電磁気〉[H24:問3]コイルのインダクタンスに関する空欄穴埋問題

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，コイルのインダクタンスに関する記述である。ここで，鉄心の磁気飽和は，無視するものとする。

均質で等断面の環状鉄心に被覆電線を巻いてコイルを作製した。このコイルの自己インダクタンスは，巻数の\( \ \fbox {　 （ア） 　} \ \)に比例し，磁路の\( \ \fbox {　 （イ） 　} \ \)に反比例する。

同じ鉄心にさらに被覆電線を巻いて別のコイルを作ると，これら二つのコイル間には相互インダクタンスが生じる。相互インダクタンスの大きさは，漏れ磁束が\( \ \fbox {　 （ウ） 　} \ \)なるほど小さくなる。それぞれのコイルの自己インダクタンスを\( \ L_{1} \ \mathrm {[H]} \ \)，\( \ L_{2} \ \mathrm {[H]} \ \)とすると，相互インダクタンスの最大値は\( \ \fbox {　 （エ） 　} \ \mathrm {[H]} \ \)である。

これら二つのコイルを\( \ \fbox {　 （オ） 　} \ \)とすると合成インダクタンスの値は，それぞれの自己インダクタンスの合計値よりも大きくなる。

上記の記述中の空白箇所(ア)，(イ)，(ウ)，(エ)及び(オ)に当てはまる組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。
\[
\begin{array}{cccccc}
& （ア） & （イ） & （ウ） & （エ） & （オ） \\
\hline
(1) & 1 \ 乗 & 断面積 & 少なく & L_{1}+L_{2} & 差動接続 \\
\hline
(2) & 2 \ 乗 & 長さ & 多く & L_{1}+L_{2} & 和動接続 \\
\hline
(3) & 1 \ 乗 & 長さ & 多く & \sqrt {L_{1}L_{2}} & 和動接続 \\
\hline
(4) & 2 \ 乗 & 断面積 & 少なく & L_{1}+L_{2} & 差動接続 \\
\hline
(5) & 2 \ 乗 & 長さ & 多く & \sqrt {L_{1}L_{2}} & 和動接続 \\
\hline
\end{array}
\]

【ワンポイント解説】

（ア）の正答を導き出せるかが最も重要となる問題です。かなりの受験生が引っ掛かる問題となるので，（ア）の導出を間違えないようにしましょう。また，非常に重要な内容となるので，確実に理解しておくようにしましょう。

1.自己インダクタンスの定義\( \ L \ \)
コイルの巻き数が\( \ N \ \)として，電流\( \ I \ \)を流した時の鎖交磁束が\( \ \phi \ \)だった時，自己インダクタンス\( \ L \ \)と鎖交磁束\( \ \phi \ \)の関係は，
\[
\begin{eqnarray}
LI&=&N\phi \\[ 5pt ] \end{eqnarray}
\] となります。

2.相互インダクタンス\( \ M \ \)
自己インダクタンス\( \ L_{1} \ \)と\( \ L_{2} \ \)のコイルがあった時の相互インダクタンス\( \ M \ \)は，
\[
\begin{eqnarray}
M&=&k\sqrt {L_{1}L_{2}} \\[ 5pt ] \end{eqnarray}
\] となります。この時，\( \ k \ \)は結合係数と呼ばれ，\( \ 0≦k≦1 \ \)となります。

3.合成インダクタンス\( \ L_{0} \ \)
自己インダクタンス\( \ L_{1} \ \left[ \mathrm{H}\right] \ \)と\( \ L_{2} \ \left[ \mathrm{H}\right] \ \)のコイルを接続した時の合成インダクタンス\( \ L_{0} \ \left[ \mathrm{H}\right] \ \)は，相互インダクタンス\( \ M \ \left[ \mathrm{H}\right] \ \)が与えられている時，以下の式で求められます。

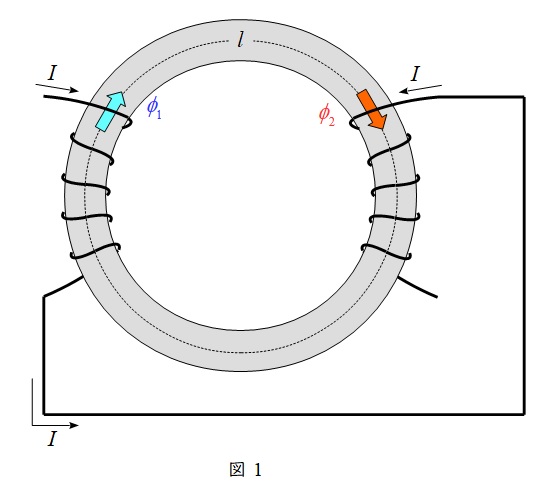
①和動接続（磁束が強め合う）時(図1)
\[
\begin{eqnarray}
L_{0}&=&L_{1}+L_{2}+2M \\[ 5pt ] \end{eqnarray}
\]

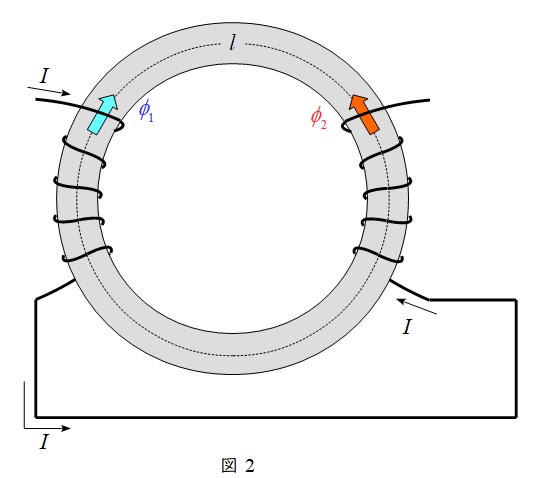
②差動接続（磁束が弱め合う）時(図2)
\[
\begin{eqnarray}
L_{0}&=&L_{1}+L_{2}-2M \\[ 5pt ] \end{eqnarray}
\]

【解答】

解答：(5)
(ア)
ワンポイント解説「1.自己インダクタンスの定義\( \ L \ \)」より，
\[
\begin{eqnarray}
LI&=&N\phi \\[ 5pt ] L&=&\frac {N\phi }{I} \\[ 5pt ] \end{eqnarray}
\] となる。ここで，\( \ \phi \ \)は磁路の断面積を\( \ S \ \)，磁束密度を\( \ B \ \)とすると，
\[
\begin{eqnarray}
\phi &=&BS \\[ 5pt ] &=&\mu HS \\[ 5pt ] &=&\frac {\mu NIS}{l} \\[ 5pt ] \end{eqnarray}
\] の関係があるため，
\[
\begin{eqnarray}
L&=&\frac {N\phi }{I} \\[ 5pt ] &=&\frac {N}{I}\times \frac {\mu NIS}{l} \\[ 5pt ] &=&\frac {\mu N^{2}S}{l} \\[ 5pt ] \end{eqnarray}
\] となり，自己インダクタンスは巻数\( \ N \ \)の\( \ 2 \ \)乗に比例する。

(イ)
(ア)の解答式の通り，自己インダクタンスは磁路の断面積\( \ S \ \)に比例し，磁路の長さ\( \ l \ \)に反比例します。

(ウ)
相互インダクタンスは，片方のコイルによる磁束がもう一方のコイルにどう影響を及ぼすかの値です。したがって，漏れ磁束が多くなるほど相互インダクタンスは小さくなります。漏れ磁束がないと結合係数\( \ k \ \)は\( \ 1 \ \)となります。

(エ)
ワンポイント解説「2.相互インダクタンス\( \ M \ \)」の通り，相互インダクタンスの最大値は，結合係数\( \ k=1 \ \)の時で，
\[
\begin{eqnarray}
M&=&\sqrt {L_{1}L_{2}} \\[ 5pt ] \end{eqnarray}
\] となります。

(オ)
ワンポイント解説「3.合成インダクタンス\( \ L_{0} \ \)」の通り，自己インダクタンスの合計値より大きくなるのは和動接続となります。