《理論》〈電気回路〉[H28:問15]交流三相電源の断線事故に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

図のように，\( \ r \ \mathrm { [ \Omega ] } \ \)の抵抗\( \ 6 \ \)個が線間電圧の大きさ\( \ V \ \mathrm { [ V ] } \ \)の対称三相電源に接続されている。\( \ b \ \)相の×印の位置で断線し，\( \ \mathrm {c-a} \ \)相間が単相状態になったとき，次の(a)及び(b)の問に答えよ。
ただし，電源の線間電圧の大きさ及び位相は，断線によって変化しないものとする。

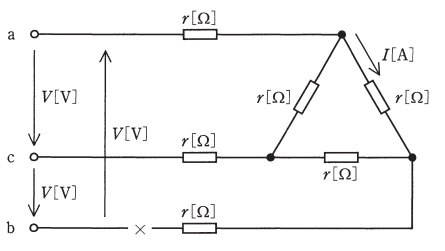
(a)　図中の電流\( \ I \ \)の大きさ\( \ \mathrm { [ A ] } \ \)は，断線前の何倍となるか。その倍率として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 0.50 \ \)　　(2)　\( \ 0.58 \ \)　　(3)　\( \ 0.87 \ \)　　(4)　\( \ 1.15 \ \)　　(5)　\( \ 1.73 \ \)

(b)　×印の両側に現れる電圧の大きさ\( \ \mathrm { [ V ] } \ \)は，電源の線間電圧の大きさ\( \ V \ \mathrm { [ V ] } \ \)の何倍となるか。その倍率として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 0 \ \)　　(2)　\( \ 0.58 \ \)　　(3)　\( \ 0.87 \ \)　　(4)　\( \ 1.00 \ \)　　(5)　\( \ 1.15 \ \)

【ワンポイント解説】

\( \ \mathrm {\Delta -Y} \ \)変換は非常によく出題されるので使いこなせるようにしておきましょう。本問のような問題はパターンを理解しておけば，ほとんどの問題を解くことができるようになると思います。過去問の類題を何題もこなし，マスターしましょう。

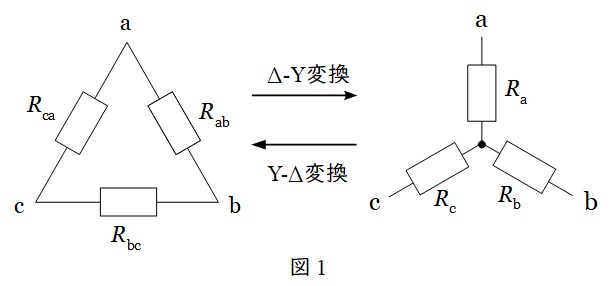
1.\( \ \mathrm {\Delta -Y} \ \)変換と\( \ \mathrm {Y-\Delta } \ \) 変換
図1において，各変換は下記の通りとなります。
①\( \ \mathrm {\Delta -Y} \ \)変換
\[
\begin{eqnarray}
R_{\mathrm {a}}=\frac {R_{\mathrm {ab}}R_{\mathrm {ca}}}{R_{\mathrm {ab}}+R_{\mathrm {bc}}+R_{\mathrm {ca}}} \\[ 5pt ] R_{\mathrm {b}}=\frac {R_{\mathrm {bc}}R_{\mathrm {ab}}}{R_{\mathrm {ab}}+R_{\mathrm {bc}}+R_{\mathrm {ca}}} \\[ 5pt ] R_{\mathrm {c}}=\frac {R_{\mathrm {ca}}R_{\mathrm {bc}}}{R_{\mathrm {ab}}+R_{\mathrm {bc}}+R_{\mathrm {ca}}} \\[ 5pt ] \end{eqnarray}
\]

②\( \ \mathrm {Y-\Delta } \ \)変換
\[
\begin{eqnarray}
R_{\mathrm {ab}}=\frac {R_{\mathrm {a}}R_{\mathrm {b}}+R_{\mathrm {b}}R_{\mathrm {c}}+R_{\mathrm {c}}R_{\mathrm {a}}}{R_{\mathrm {c}}} \\[ 5pt ] R_{\mathrm {bc}}=\frac {R_{\mathrm {a}}R_{\mathrm {b}}+R_{\mathrm {b}}R_{\mathrm {c}}+R_{\mathrm {c}}R_{\mathrm {a}}}{R_{\mathrm {a}}} \\[ 5pt ] R_{\mathrm {ca}}=\frac {R_{\mathrm {a}}R_{\mathrm {b}}+R_{\mathrm {b}}R_{\mathrm {c}}+R_{\mathrm {c}}R_{\mathrm {a}}}{R_{\mathrm {b}}} \\[ 5pt ] \end{eqnarray}
\]

【関連する「電気の神髄」記事】

　　Y⇔Δ回路のインピーダンス変換式

【解答】

(a)解答：(1)
断線前の問題図の負荷を\( \ \mathrm {\Delta -Y} \ \)変換すると，図2のようになるので，一相分等価回路は図3のようになる。


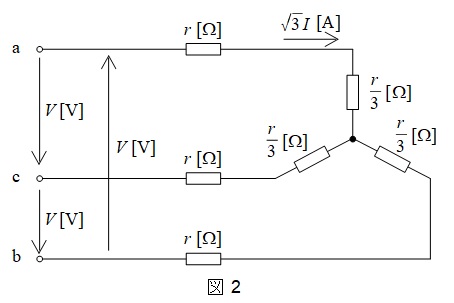
図3より，電流\( \ I \ \)は，
\[
\begin{eqnarray}
\sqrt {3}I=\frac {\displaystyle \frac {V}{\sqrt {3}}}{\displaystyle r+\frac {r}{3}} \\[ 5pt ] ⇔I=\frac {V}{4r} \\[ 5pt ] \end{eqnarray}
\] と求められる。また，断線後の回路は図4のように描くことができる。

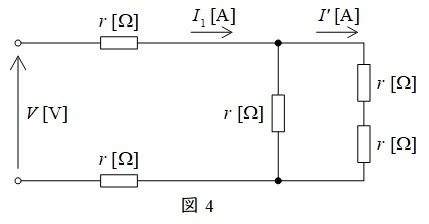
図4における合成抵抗\( \ R \ \)は，
\[
\begin{eqnarray}
R&=&r+\frac {r\cdot 2r}{r+2r} +r \\[ 5pt ] &=&\frac {8}{3}r
\end{eqnarray}
\] となる。よって，図4に示す電流\( \ I_{1} \ \)は，
\[
\begin{eqnarray}
I_{1}&=&\frac {V}{R} \\[ 5pt ] &=&\frac {V}{\displaystyle \frac {8}{3}r} \\[ 5pt ] &=&\frac {3V}{8r}
\end{eqnarray}
\] と求められる。\( \ I^{\prime } \ \)は，\( \ r \ \)と\( \ 2r \ \)の分流比であるので，
\[
\begin{eqnarray}
I^{\prime }&=&\frac {r}{r+2r}I_{1} \\[ 5pt ] &=&\frac {r}{r+2r}\times \frac {3V}{8r} \\[ 5pt ] &=&\frac {V}{8r}
\end{eqnarray}
\] と求められる。したがって，断線前後の電流の大きさの比は，
\[
\begin{eqnarray}
\frac {I^{\prime }}{I}&=&\frac {\displaystyle \frac {V}{8r}}{\displaystyle \frac {V}{4r}} \\[ 5pt ] &=&\frac {1}{2}=0.5
\end{eqnarray}
\] と求められる。

(b)解答：(3)
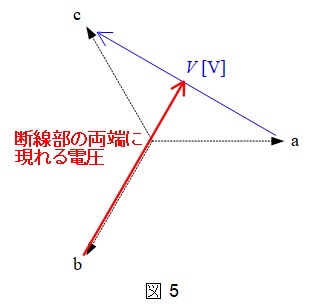
断線後の電圧ベクトル図を描くと図5のようになる。ここで，×印の両側に現れる電圧は，\( \ \mathrm {a} \ \)と\( \ \mathrm {c} \ \)の中間部の電位と\( \ \mathrm {b} \ \)の電位差となるので，ベクトル図においては赤矢印の電圧がその大きさとなる。線間電圧の大きさが\( \ V \ \mathrm {[V]} \ \)であるとすると断線部の両端に現れる電圧は\( \ \displaystyle \frac {\sqrt {3}}{2}V \ \mathrm {[V]} \ \)となるので，
\[
\begin{eqnarray}
\cfrac {\cfrac {\sqrt {3}}{2}V}{V}&=&\frac {\sqrt {3}}{2} \\[ 5pt ] &≒&0.87 \\[ 5pt ] \end{eqnarray}
\] と求められる。