《理論》〈電気回路〉[H21:問8]交流回路のスイッチ開放前後の電流の特性に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

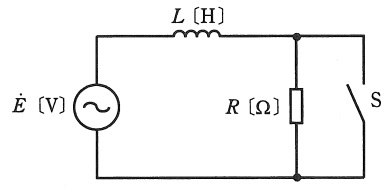
図のように，\( \ R=\sqrt {3}\omega L \ \mathrm {[\Omega ]} \ \)の抵抗，インダクタンス\( \ L \ \mathrm {[H]} \ \)のコイル，スイッチ\( \ \mathrm {S} \ \)が角周波数\( \ \omega \ \mathrm {[rad / s]} \ \)の交流電圧\( \ \dot E \ \mathrm{[V]} \ \)の電源に接続されている。スイッチ\( \ \mathrm {S} \ \)を開いているとき，コイルを流れる電流の大きさを\( \ I_{1} \ \mathrm {[A]} \ \)，電源電圧に対する電流の位相差を\( \ \theta _{1} \ \mathrm {[°]} \ \)とする。また，スイッチ\( \ \mathrm {S} \ \)を閉じているとき，コイルを流れる電流の大きさを\( \ I_{2} \ \mathrm {[A]} \ \)，電源電圧に対する電流の位相差を\( \ \theta _{2} \ \mathrm {[°]} \ \)とする。このとき，\( \ \displaystyle \frac {I_{1}}{I_{2}} \ \)及び\( \ \left| \theta _{1}-\theta _{2}\right| \ \mathrm {[°]} \ \)の値として，正しいものを組み合わせたのは次のうちどれか。

\[
\begin{array}{ccc}
& \displaystyle \frac {I_{1}}{I_{2}} & \left| \theta _{1}-\theta _{2}\right| \\
\hline
(1) & \displaystyle \frac {1}{2} & 30 \\
\hline
(2) & \displaystyle \frac {1}{2} & 60 \\
\hline
(3) & 2 & 30 \\
\hline
(4) & 2 & 60 \\
\hline
(5) & 2 & 90 \\
\hline
\end{array}
\]

【ワンポイント解説】

抵抗とインダクタンスを接続した交流回路のスイッチ開放前後の電流の特性に関する問題です。
解答においては受験生が考えやすい直交座標を使用した複素数で解いていますが，慣れてきたら大きさと位相を分けて極座標で解く方法も計算量が少なくなるため有効かと思います。

1.抵抗，コイル，コンデンサの電圧\( \ V \ \mathrm {[V]} \ \)と電流\( \ I \ \mathrm {[A]} \ \)の関係
抵抗\( \ R \ \mathrm {[\Omega ]} \ \)，コイル\( \ L \ \mathrm {[H]} \ \)，コンデンサ\( \ C \ \mathrm {[F]} \ \)があり，電源の角周波数\( \ \omega \ \mathrm {[rad / s]} \ \)及び周波数\( \ f \ \mathrm {[Hz]} \ \)が与えられているとき，それぞれのインピーダンスは，
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {R}}&=&R&& \\[ 5pt ] {\dot Z}_{\mathrm {L}}&=&\mathrm {j}\omega L&=&\mathrm {j}2\pi f L \\[ 5pt ] {\dot Z}_{\mathrm {C}}&=&\frac {1}{\mathrm {j}\omega C}&=&\frac {1}{\mathrm {j}2\pi f C} \\[ 5pt ] \end{eqnarray}
\] で求められ，それぞれの電圧と電流の関係は，
\[
\begin{eqnarray}
{\dot V}_{\mathrm {R}}&=&R\dot I \\[ 5pt ] {\dot V}_{\mathrm {L}}&=&\mathrm {j}\omega L \dot I \\[ 5pt ] {\dot V}_{\mathrm {C}}&=&\frac {\dot I }{\mathrm {j}\omega C} \\[ 5pt ] \end{eqnarray}
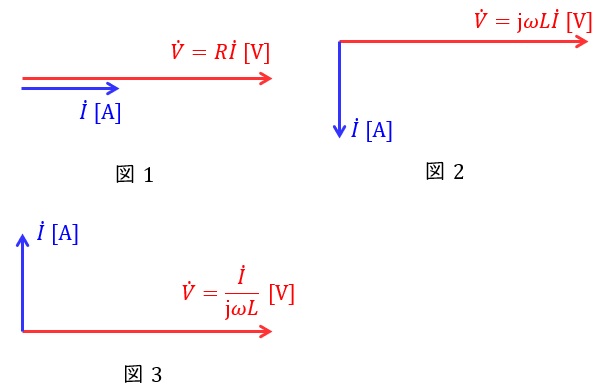
\] となります。この関係をベクトル図に表すと，図1～図3となります。

【解答】

解答：(2)
スイッチ\( \ \mathrm {S} \ \)を開いているときのインピーダンス\( \ \dot Z \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
\dot Z&=&R+\mathrm {j}\omega L \\[ 5pt ] &=&\sqrt {3}\omega L+\mathrm {j}\omega L \\[ 5pt ] &=&\omega L\left( \sqrt {3}+\mathrm {j}\right) \\[ 5pt ] \end{eqnarray}
\] なので，電流\( \ {\dot I}_{1} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
{\dot I}_{1}&=&\frac {\dot E}{\dot Z} \\[ 5pt ] &=&\frac {\dot E}{\omega L\left( \sqrt {3}+\mathrm {j}\right) } \\[ 5pt ] &=&\frac {\dot E}{\omega L\left( \sqrt {3}+\mathrm {j}\right) }\cdot \frac {\sqrt {3}-\mathrm {j}}{\sqrt {3}-\mathrm {j}} \\[ 5pt ] &=&\frac {\dot E}{\omega L\left( 3+1\right) }\left( \sqrt {3}-\mathrm {j}\right) \\[ 5pt ] &=&\frac {\dot E}{4\omega L}\left( \sqrt {3}-\mathrm {j}\right) \\[ 5pt ] \end{eqnarray}
\] となる。ここで，\( \dot E \ \)を基準とすると\( \dot E=E \ \)であるから，\( \ {\dot I}_{1} \ \mathrm {[A]} \ \)の大きさ\( \ I_{1} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{1}&=&\frac {E}{4\omega L}\sqrt { \left( \sqrt {3}\right) ^{2}+1^{2}} \\[ 5pt ] &=&\frac {E}{2\omega L} \\[ 5pt ] \end{eqnarray}
\] となる。一方，スイッチ\( \ \mathrm {S} \ \)を閉じているときの電流\( \ {\dot I}_{2} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
{\dot I}_{2}&=&\frac {\dot E}{\mathrm {j}\omega L} \\[ 5pt ] &=&-\mathrm {j}\frac {\dot E}{\omega L} \\[ 5pt ] \end{eqnarray}
\] となるので，その大きさ\( \ I_{2} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{2}&=&\frac {E}{\omega L} \\[ 5pt ] \end{eqnarray}
\] となる。以上から，\( \ \displaystyle \frac {I_{1}}{I_{2}} \ \)は，
\[
\begin{eqnarray}
\frac {I_{1}}{I_{2}}&=&\frac {\displaystyle \frac {E}{2\omega L}}{\displaystyle \frac {E}{\omega L}} \\[ 5pt ] &=&\frac {1}{2} \\[ 5pt ] \end{eqnarray}
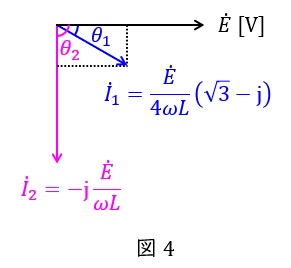
\] であり，\( \ {\dot I}_{1} \ \mathrm {[A]} \ \)と\( \ {\dot I}_{2} \ \mathrm {[A]} \ \)をベクトル図で示すと図4のようになるため，位相差\( \ \left| \theta _{1}-\theta _{2}\right| \ \mathrm {[°]} \ \)は\( \ 60° \ \)と求められる。

【別解】
スイッチ\( \ \mathrm {S} \ \)を開いているときのインピーダンス\( \ \dot Z \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
\dot Z&=&R+\mathrm {j}\omega L \\[ 5pt ] &=&\sqrt {3}\omega L+\mathrm {j}\omega L \\[ 5pt ] &=&2\omega L∠30° \\[ 5pt ] \end{eqnarray}
\] なので，電流\( \ {\dot I}_{1} \ \mathrm {[A]} \ \)は，\( \dot E=E∠0° \ \)を基準とすると，
\[
\begin{eqnarray}
{\dot I}_{1}&=&\frac {\dot E}{\dot Z} \\[ 5pt ] &=&\frac {E∠0°}{\displaystyle 2\omega L∠30°} \\[ 5pt ] &=&\frac {E}{2\omega L}∠\left( -30° \right) \\[ 5pt ] \end{eqnarray}
\] となる。一方，スイッチ\( \ \mathrm {S} \ \)を閉じているときの電流\( \ {\dot I}_{2} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
{\dot I}_{2}&=&\frac {\dot E}{\mathrm {j}\omega L} \\[ 5pt ] &=&\frac {E∠0°}{\omega L∠90°} \\[ 5pt ] &=&\frac {E}{\omega L}∠\left( -90° \right) \\[ 5pt ] \end{eqnarray}
\] となるので，大きさの比\( \ \displaystyle \frac {I_{1}}{I_{2}} \ \)は，
\[
\begin{eqnarray}
\frac {I_{1}}{I_{2}}&=&\frac {\displaystyle \frac {E}{2\omega L}}{\displaystyle \frac {E}{\omega L}} \\[ 5pt ] &=&\frac {1}{2} \\[ 5pt ] \end{eqnarray}
\] であり，位相差\( \ \left| \theta _{1}-\theta _{2}\right| \ \mathrm {[°]} \ \)は，
\[
\begin{eqnarray}
\left| \theta _{1}-\theta _{2}\right| &=&\left| -30°-\left( -90°\right) \right| \\[ 5pt ] &=&60 \ \mathrm {[°]} \\[ 5pt ] \end{eqnarray}
\] と求められる。