《理論》〈電子理論〉[H21:問12]磁界中及び電界中の電子の運動に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

図1のように，真空中において強さが一定で一様な磁界中に，速さ\( \ v \ \mathrm {[m/s]} \ \)の電子が磁界の向きに対して\( \ \theta \ \mathrm {[°]} \ \)の角度\( \ \left( 0 \ \mathrm {[°]}＜\theta \ \mathrm {[°]}＜90 \ \mathrm {[°]}\right) \ \)で突入した。この場合，電子は進行方向にも磁界の向きにも\( \ \fbox {　 （ア） 　} \ \)方向の電磁力を常に受けて，その軌跡は，\( \ \fbox {　 （イ） 　} \ \)を描く。

次に，電界中に電子を置くと，電子は電界の向きと\( \ \fbox {　 （ウ） 　} \ \)方向の静電力を受ける。また，図2のように，強さが一定で一様な電界中に，速さ\( \ v \ \mathrm {[m/s]} \ \)の電子が電界の向きに対して\( \ \theta \ \mathrm {[°]} \ \)の角度\( \ \left( 0 \ \mathrm {[°]}＜\theta \ \mathrm {[°]}＜90 \ \mathrm {[°]}\right) \ \)で突入したとき，その軌跡は，\( \ \fbox {　 （エ） 　} \ \)を描く。

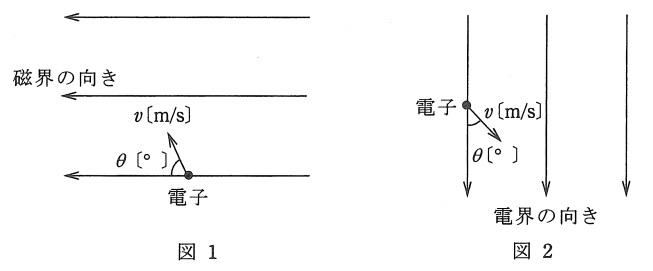
上記の記述中の空白箇所(ア)，(イ)，(ウ)及び(エ)に当てはまる語句として，正しいものを組み合わせたのは次のうちどれか。

\[
\begin{array}{ccccc}
& （ア） & （イ） & （ウ） & （エ） \\
\hline
(1) & 　反　対　 & 　らせん　 & 　反　対　 & 　放物線　 \\
\hline
(2) & 　直　角　 & 　円　　　 & 　同　じ　 & 　円　　　 \\
\hline
(3) & 　同　じ　 & 　円　　　 & 　直　角　 & 　放物線　 \\
\hline
(4) & 　反　対　 & 　らせん　 & 　同　じ　 & 　円　　　 \\
\hline
(5) & 　直　角　 & 　らせん　 & 　反　対　 & 　放物線　 \\
\hline
\end{array}
\]

【ワンポイント解説】

真空中の電子の運動に関する問題です。
電界と磁界，非常に似た性質もありますが，電荷に加わる力は全く違います。違いを理解するには非常に良い問題と思いますので，必ず理解しておくようにしましょう。

1.電荷に働く力の大きさ
一様な電界\( \ E \ \mathrm {[V / m]} \ \)が電荷\( \ q \ \mathrm {[C]} \ \)にかかっているとき，この電荷\( \ q \ \mathrm {[C]} \ \)に働く力の大きさ\( \ F \ \mathrm {[N]} \ \)は，
\[
\begin{eqnarray}
F &=&qE \\[ 5pt ] \end{eqnarray}
\] となります。電子の場合は，電荷がマイナスなので，電界と逆方向の力が加わります。

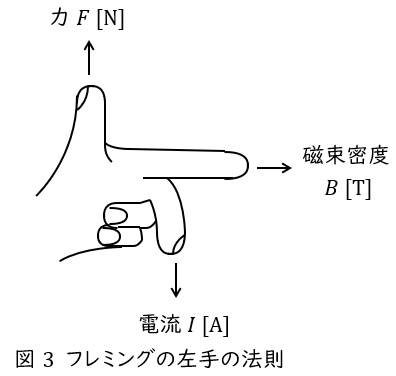
2.フレミングの左手の法則
中指を電流の向き，人差し指を磁界の向きに合わせると，親指の方向に力が働くという法則で，頭文字を取って「電磁力」と覚えます。
磁束密度の大きさ\( \ B \ \mathrm {[T]} \ \)，電子の速度\( \ v \ \mathrm {[m/s]} \ \)，電子の電荷を\( \ e \ \mathrm {[C]} \ \)とすると，電子にかかるローレンツ力\( \ F \ \mathrm {[N]} \ \)は，
\[
\begin{eqnarray}
F &=&evB \\[ 5pt ] \end{eqnarray}
\] となります。電子の場合，動く向きが電流の向きと逆になるので，中指の向きに注意するようにしましょう。

【解答】

解答：(5)
(ア)
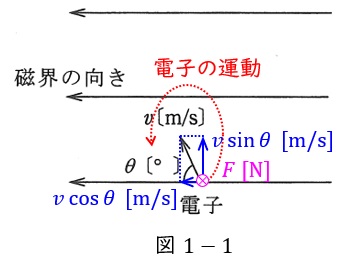
図1の電子の速度を磁界と同方向成分\( \ v \cos \theta \ \)と磁界と直角方向成分\( \ v \sin \theta \ \)に分けると，電子に力が加わるのは直角成分のみであり，その向きはワンポイント解説「2.フレミングの左手の法則」の通り，手前から奥の向きとなります。

(イ)
磁界と直角方向成分\( \ v \sin \theta \ \)に対しては常に動く方向と直角方向に力が加わり円運動，磁界と同方向成分\( \ v \cos \theta \ \)に対しては電子に力が加わらないため一定の速度\( \ v \cos \theta \ \)で動きます。したがって，全体としてはらせん運動となります。

(ウ)
ワンポイント解説「1.電荷に働く力の大きさ」の通り，電界中に電子を置くと，電子は電界の向きと反対方向に静電力を受けます。

(エ)
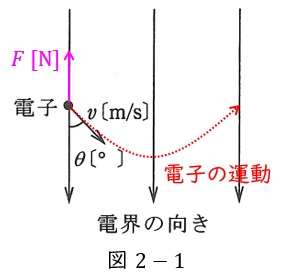
図2-1に示すように，電子は常に上向きの力を受けるため，放物線を描くようになります。