《理論》〈電磁気〉[H21:問4]扇形導線が作る磁界の大きさに関する計算問題

【問題】

【難易度】★★★☆☆（普通）

図のように，点\( \ \mathrm {O} \ \)を中心とするそれぞれ半径\( \ 1 \ \mathrm {[m]} \ \)と半径\( \ 2 \ \mathrm {[m]} \ \)の円形導線の\( \ \displaystyle \frac {1}{4} \ \)とそれらを連結する直線状の導線からなる扇形導線がある。この導線に，図に示す向きに直流電流\( \ I=8 \ \mathrm {[A]} \ \)を流した場合，点\( \ \mathrm {O} \ \)における磁界\( \ \mathrm {[A / m]} \ \)の大きさとして，正しいのは次のうちどれか。

ただし，扇形導線は同一平面上にあり，その巻数は一巻きである。

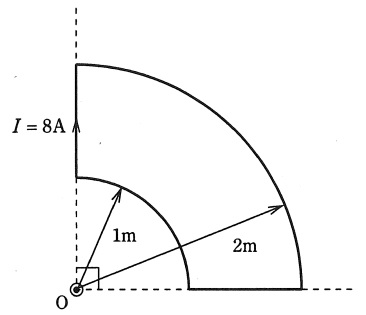
　(1)　\( \ 0.25 \ \)　　(2)　\( \ 0.5 \ \)　　(3)　\( \ 0.75 \ \)　　(4)　\( \ 1.0 \ \)　　(5)　\( \ 2.0 \ \)

【ワンポイント解説】

扇形導線が作る磁界の大きさを求める問題です。
もちろんビオ・サバールの法則を知っていて導出できるのが理想ですが，\( \ 3 \ \)種の出題範囲外である積分計算を伴うため，問題を解く上では円形コイルが作る磁界の大きさの公式を覚えておいて解くのが良いかと思います。

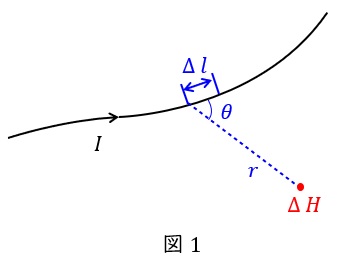
1.ビオ・サバールの法則
図1に示すように，微小な長さ\( \ \Delta l \ \)に流れる電流\( \ I \ \)が，距離\( \ r \ \)離れた場所に作る磁界\( \ \Delta H \ \)は，
\[
\begin{eqnarray}
\Delta H&=&\frac {I \Delta l}{4\pi r^{2}}\sin \theta \\[ 5pt ] \end{eqnarray}
\] となります。

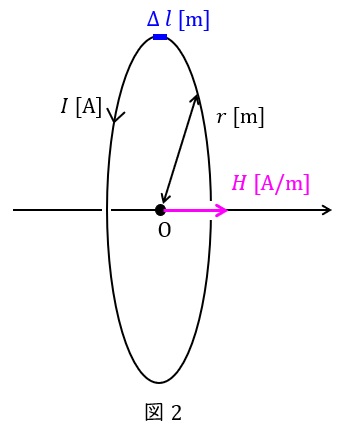
2.円形コイルが中心点に作る磁界の大きさ
ビオ・サバールの法則を図2のような円形コイルに適用すると，コイルの長さが\( \ 2 \pi r \ \)であり，中心点\( \ \mathrm {O} \ \)から見た微小電流の角度\( \ \theta \ \)は常に\( \ 90° \ \)であるから，
\[
\begin{eqnarray}
H&=&\frac {I \times 2\pi r}{4\pi r^{2}}\sin 90° \\[ 5pt ] &=&\frac {I}{2r} \\[ 5pt ] \end{eqnarray}
\] となります。（この結果は公式として覚えておきましょう。）

【解答】

解答：(2)
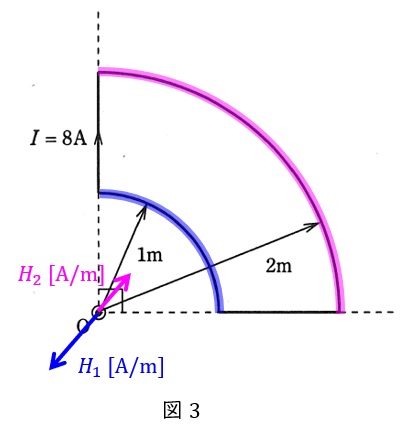
ワンポイント解説「1.ビオ・サバールの法則」の通り，直線状の導線と点\( \ \mathrm {O} \ \)のなす角は\( \ 0° \ \)であるため，点\( \ \mathrm {O} \ \)の磁界に影響を与えるのは扇形導線のみである。
半径\( \ r_{1}=1 \ \mathrm {[m]} \ \)の扇形導線が作る磁界を\( \ H_{1} \ \mathrm {[A / m]} \ \)，半径\( \ r_{2}=2 \ \mathrm {[m]} \ \)の扇形導線が作る磁界を\( \ H_{2} \ \mathrm {[A / m]} \ \)とすると，電流の向きが逆であるから，磁界の向きも逆となり図3のようになる。
それぞれの大きさ\( \ H_{1} \ \mathrm {[A / m]} \ \)及び\( \ H_{2} \ \mathrm {[A / m]} \ \)は，ワンポイント解説「2.円形コイルが中心点に作る磁界の大きさ」の通り，
\[
\begin{eqnarray}
H_{1}&=&\frac {I}{2r_{1}}\times \frac {1}{4} \\[ 5pt ] &=&\frac {8}{2\times 1}\times \frac {1}{4} \\[ 5pt ] &=&1.0 \ \mathrm {[A / m]} \\[ 5pt ] H_{2}&=&\frac {I}{2r_{2}}\times \frac {1}{4} \\[ 5pt ] &=&\frac {8}{2\times 2}\times \frac {1}{4} \\[ 5pt ] &=&0.5 \ \mathrm {[A / m]} \\[ 5pt ] \end{eqnarray}
\] であるから，点\( \ \mathrm {O} \ \)の磁界の大きさ\( \ H \ \mathrm {[A / m]} \ \)は，
\[
\begin{eqnarray}
H&=&H_{1}-H_{2} \\[ 5pt ] &=&1.0-0.5 \\[ 5pt ] &=&0.5 \ \mathrm {[A / m]} \\[ 5pt ] \end{eqnarray}
\] と求められる。