《理論》〈電子理論〉[R2:問13]演算増幅器及びそれを用いた回路に関する論説問題

【問題】

【難易度】★★★★☆（やや難しい）

演算増幅器及びそれを用いた回路に関する記述として，誤っているものを次の(1)～(5)のうちから一つ選べ。

(1)　演算増幅器には電源が必要である。

(2)　演算増幅器の入力インピーダンスは，非常に大きい。

(3)　演算増幅器は比較器として用いられることがある。

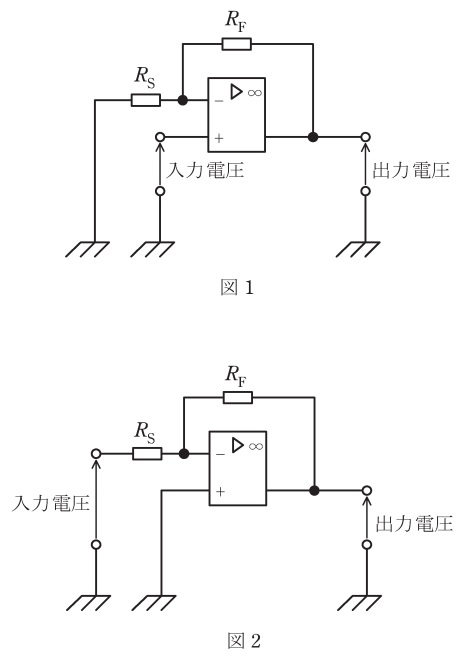
(4)　図1の回路は正相増幅回路，図2の回路は逆相増幅回路である。

(5)　図1の回路は，抵抗\( \ R_{\mathrm {S}} \ \)を\( \ 0 \ \mathrm {\Omega } \ \)に（短絡）し，抵抗\( \ R_{\mathrm {F}} \ \)を\( \ \infty \ \mathrm {\Omega } \ \)に（開放）すると，ボルテージホロワである。

【ワンポイント解説】

演算増幅器に関する問題です。演算増幅器は計算問題の方が出題されやすいですが，稀に誤答選択問題も出題されることがあります。ボルテージホロワは私も２種の勉強時に知った気がするので，３種のテキストにはあまり記載がない内容かもしれません。

1.理想的な演算増幅器の特徴
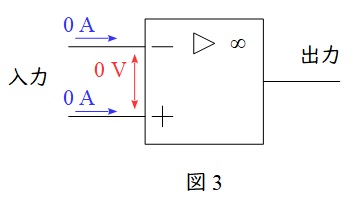
　１．電圧増幅率が無限大である。したがって，無限大でない有限数が出力される時，入力端子間の電圧は\( \ 0 \ \mathrm {V} \ \)(バーチャルショート)となる。
　２．入力インピーダンスが無限大である。したがって入力端子に電流は流れない。
　３．出力インピーダンスがゼロである。

2.ボルテージホロワ回路
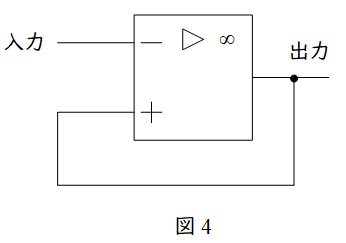
図4のように入力端子の＋と出力端子を接続したものをボルテージホロワ回路と言います。
これにより，仮に入力電圧\( \ V_{\mathrm {i}} \ \)が入ってきたとき，仮想短絡により入力の＋端子も\( \ V_{\mathrm {i}} \ \)となり，入力と出力の大きさが等しくなります。
したがって，ボルテージホロワ回路は電圧増幅率が\( \ 1 \ \)の回路と言えます。
一見無駄な回路に見えますが，入力と出力を縁切りできることで，外乱による影響等を抑制することが可能となります。

【解答】

解答：(5)
(1)正しい
演算増幅器は電圧を増幅させる素子で，電源がないと働きません。

(2)正しい
ワンポイント解説「1.理想的な演算増幅器の特徴」の通り，演算増幅器の入力インピーダンスは非常に大きく，理想的には無限大です。

(3)正しい
演算増幅器は入力端子の＋と−の大きさの違いに応じて出力が切換わる比較器の役割があります。（電験ではあまり出題されません。）

(4)正しい
図１に入力電圧\( \ V_{\mathrm {i}} \ \)が入ってきたとき，−端子も\( \ V_{\mathrm {i}} \ \)となり，\( \ R_{\mathrm {S}} \ \)を流れる電流\( \ I \ \)が，
\[
\begin{eqnarray}
I&=&\frac {V_{\mathrm {i}}}{R_{\mathrm {S}}} \\[ 5pt ] \end{eqnarray}
\] となります。演算増幅器には電流は流れないので，\( \ R_{\mathrm {S}} \ \)を流れる電流と\( \ R_{\mathrm {F}} \ \)を流れる電流は等しく，出力電圧\( \ V_{\mathrm {o}} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {o}} &=&\frac {R_{\mathrm {F}}}{R_{\mathrm {S}}}V_{\mathrm {i}} \\[ 5pt ] \end{eqnarray}
\] となります。したがって，図１は正相増幅回路となります。
同様に図２に入力電圧\( \ V_{\mathrm {i}} \ \)が入ってきたとき，出力電圧\( \ V_{\mathrm {o}} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {o}} &=&-\frac {R_{\mathrm {F}}}{R_{\mathrm {S}}}V_{\mathrm {i}} \\[ 5pt ] \end{eqnarray}
\] となり，図２は逆相増幅回路となります。

(5)誤り
ワンポイント解説「2.ボルテージホロワ回路」の通り，ボルテージホロワ回路は入力電圧と出力電圧が等しくなる回路のことで，図1の回路でボルテージホロワ回路を実現するためには，抵抗\( \ \underline {R_{\mathrm {S}}} \ \)を\( \ \underline {\infty \ \mathrm {\Omega }} \ \)に（開放）し，抵抗\( \ \underline {R_{\mathrm {F}}} \ \)を\( \ \underline {0 \ \mathrm {\Omega }} \ \)に（短絡）すると，入力電圧と出力電圧が等しくなります。