《理論》〈電磁気〉[H22:問3]一様磁界中で導体棒を動かした場合の誘導電流の導出に関する計算問題

【問題】

【難易度】★☆☆☆☆（易しい）

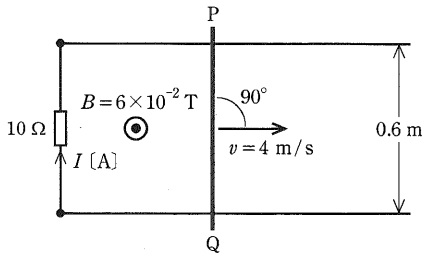
紙面に平行な水平面内において，\( \ 0.6 \ \mathrm {[m]} \ \)の間隔で張られた\( \ 2 \ \)本の直線状の平行導線に\( \ 10 \ \mathrm {[\Omega ]} \ \)の抵抗が接続されている。この平行導線に垂直に，図に示すように，直線状の導体棒\( \ \mathrm {PQ} \ \)を渡し，紙面の裏側から表側に向かって磁束密度\( \ B = 6\times 10^{-2} \mathrm {[T]} \ \)の一様な磁界をかける。 ここで，導体棒\( \ \mathrm {PQ} \ \)を磁界と導体棒に共に垂直な矢印の方向に一定の速さ\( \ v=4 \ \mathrm {[m / s]} \ \)で平行導線上を移動させているときに，\( \ 10 \ \mathrm {[\Omega ]} \ \)の抵抗に流れる電流\( \ I \ \mathrm {[A]} \ \)の値として，正しいのは次のうちどれか。

ただし，電流の向きは図に示す矢印の向きを正とする。 また，導線及び導体棒\( \ \mathrm {PQ} \ \)の抵抗，並びに導線と導体棒との接触抵抗は無視できるものとする。

　(1)　\( \ -0.0278 \ \)　　(2)　\( \ -0.0134 \ \)　　(3)　\( \ -0.0072 \ \)　　(4)　\( \ 0.0144 \ \)　
　(5)　\( \ 0.0288 \ \)　　

【ワンポイント解説】

導体棒を動かした場合に生じる誘導起電力から回路に流れる電流を求める問題です。
あらゆる電験のテキストに掲載されている内容なので，確実に得点できるように準備しておきましょう。
また，フレミングの法則を勉強する際には，左手の法則と右手の法則，どちらのパターンの問題が出題されても毎回両方の法則を確認するようにして下さい。

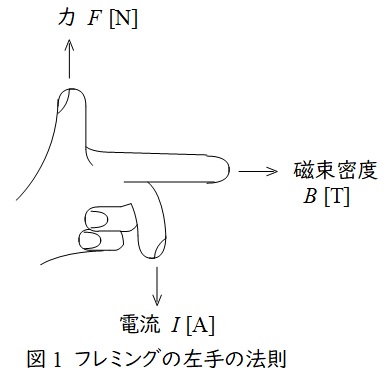
1.フレミングの左手の法則
中指を電流の向き，人差し指を磁界の向きに合わせると，親指の方向に力が働くという法則で，頭文字を取って「電磁力」と覚えます。
磁束密度の大きさ\( \ B \ \mathrm {[T]} \ \)，電流の大きさ\( \ I \ \mathrm {[A]} \ \)，直線状導体の長さを\( \ l \ \mathrm {[m]} \ \)とすると，導体に発生する電磁力\( \ F \ \mathrm {[N]} \ \)は，
\[
\begin{eqnarray}
F &=&BIl \\[ 5pt ] \end{eqnarray}
\] となります。

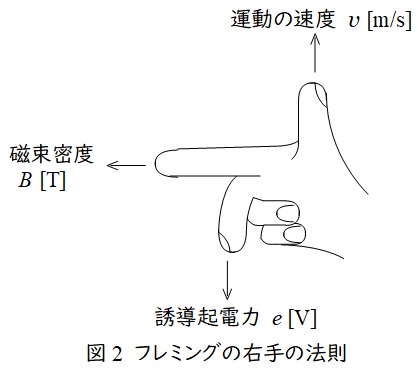
2.フレミングの右手の法則
親指を導体の運動方向，人差し指を磁界（磁束密度）の方向にすると，中指の方向に誘導起電力が発生するという法則で，磁束密度の大きさを\( \ B \ \mathrm {[T]} \ \)，導体の速度を\( \ v \ \mathrm {[m／s]} \ \)，導体の長さを\( \ l \ \mathrm {[m]} \ \)とすると，誘導起電力の大きさ\( \ e \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
e &=& Blv \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(4)
ワンポイント解説「2.フレミングの右手の法則」の通り，右手の親指の方向を運動方向で左から右，人差し指の方向を奥から手前とすると，中指は\( \ \mathrm {P} \ \)から\( \ \mathrm {Q} \ \)の向きになるので，誘導起電力は\( \ \mathrm {P} \ \)から\( \ \mathrm {Q} \ \)の向きが正となり，\( \ 10 \ \mathrm {[\Omega ]} \ \)の抵抗に流れる電流\( \ I \ \mathrm {[A]} \ \)は上向きとなる。
誘導起電力\( \ e \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
e &=& Blv \\[ 5pt ] &=& 6\times 10^{-2}\times 0.6\times 4 \\[ 5pt ] &=& 0.144 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となるので，\( \ 10 \ \mathrm {[\Omega ]} \ \)の抵抗に流れる電流\( \ I \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I &=& \frac {e}{R} \\[ 5pt ] &=& \frac {0.144}{10} \\[ 5pt ] &=& 0.0144 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。