《理論》〈電気回路〉[H26:問7]直流回路の消費電力に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

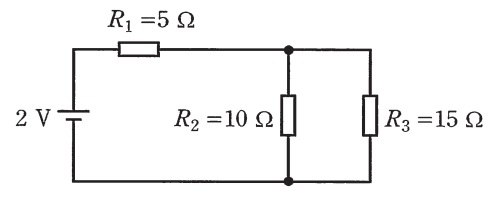
図に示す直流回路において，抵抗\(R_{1}=5 \ \Omega \)で消費される電力は抵抗\(R_{3}=15 \ \Omega \)で消費される電力の何倍となるか。その倍率として，最も近い値を次の(1)～(5)のうちから一つ選べ。

(1)　\(0.9\)　　(2)　\(1.2\)　　(3)　\(1.5\)　　(4)　\(1.8\)　　(5)　\(2.1\)

【ワンポイント解説】

分流の計算と合成抵抗の計算，消費電力の計算の基本公式をすべて理解していることを問う問題です。いずれも基本公式なので，よく理解しておいて下さい。

1.並列回路の分流の計算
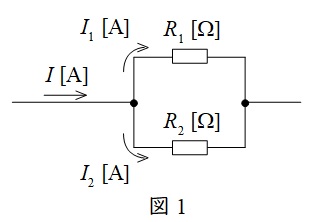
図1のような回路がある時，\(R_{1}\)及び\(R_{2}\)に流れる電流\(I_{1}\)，\(I_{2}\)は，
\[
\begin{eqnarray}
I_{1}&=&\frac {R_{2}}{R_{1}+R_{2}}I \\[ 5pt ] I_{2}&=&\frac {R_{1}}{R_{1}+R_{2}}I \\[ 5pt ] \end{eqnarray}
\] となります。

2.並列回路の合成抵抗
図1のような回路が与えられている時，\(R_{1}\)と\(R_{2}\)の合成抵抗\(R\)は，
\[
\begin{eqnarray}
\frac {1}{R}&=&\frac {1}{R_{1}}+\frac {1}{R_{2}} \\[ 5pt ] R&=&\frac {R_{1}R_{2}}{R_{1}+R_{2}} \\[ 5pt ] \end{eqnarray}
\] で求められます。

3.抵抗での消費電力
抵抗\(R\)に電圧\(V\)がかかっており，電流\(I\)が流れている時，抵抗での消費電力\(P\)は，
\[
\begin{eqnarray}
P&=&RI^{2} \\[ 5pt ] &=&VI \\[ 5pt ] &=&\frac {V^{2}}{R} \\[ 5pt ] \end{eqnarray}
\] で求められます。

【解答】

解答：(5)
ワンポイント解説「2.並列回路の合成抵抗」より，\(R_{2}\)と\(R_{3}\)の合成抵抗\(R_{23}\)は，
\[
\begin{eqnarray}
R_{23}&=&\frac {R_{2}R_{3}}{R_{2}+R_{3}} \\[ 5pt ] &=&\frac {10\times 15}{10+15} \\[ 5pt ] &=&6 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となるので，\(R_{1}\)，\(R_{2}\)，\(R_{3}\)の合成抵抗\(R\)は，
\[
\begin{eqnarray}
R&=&R_{1}+R_{23} \\[ 5pt ] &=&5+6 \\[ 5pt ] &=&11 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。よって，\(R_{1}\)に流れる電流\(I_{1}\)は，
\[
\begin{eqnarray}
I_{1}&=&\frac {2}{R} \\[ 5pt ] &=&\frac {2}{11} \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となるので，ワンポイント解説「3.抵抗での消費電力」より\(R_{1}\)での消費電力\(P_{1}\)は，
\[
\begin{eqnarray}
P_{1}&=&R_{1}I_{1}^{2} \\[ 5pt ] &=&5\times \left( \frac {2}{11}\right) ^{2} \\[ 5pt ] &=&\frac {20}{121} \ \mathrm {[W ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。また，抵抗\(R_{3}\)にかかる電圧\(V_{3}\)は，
\[
\begin{eqnarray}
V_{3}&=&\frac {R_{23}}{R_{1}+R_{23}}\times 2 \\[ 5pt ] &=&\frac {6}{5+6}\times 2 \\[ 5pt ] &=&\frac {12}{11} \ \mathrm {[V ]} \\[ 5pt ] \end{eqnarray}
\] となるので，抵抗\(R_{3}\)での消費電力\(P_{3}\)は，
\[
\begin{eqnarray}
P_{3}&=&\frac {V_{3}^{2}}{R_{3}} \\[ 5pt ] &=&\frac {\left( \frac {12}{11}\right) ^{2}}{15} \\[ 5pt ] &=&\frac {144}{121\times 15} \ \mathrm {[W ]} \\[ 5pt ] \end{eqnarray}
\] となる。よって，\(R_{1}\)と\(R_{3}\)の消費電力の比は，
\[
\begin{eqnarray}
\frac {P_{1}}{P_{3}}&=&\frac {\displaystyle \frac {20}{121}}{\displaystyle \frac {144}{121\times 15}} \\[ 5pt ] &=&\frac {20\times 15}{144} \\[ 5pt ] &≒&2.08　→　2.1 \\[ 5pt ] \end{eqnarray}
\] と求められる。