Contents
【問題】
【難易度】★★★★☆(やや難しい)
電力計について,次の(a)及び(b)の問に答えよ。
(a) 次の文章は,電力計の原理に関する記述である。
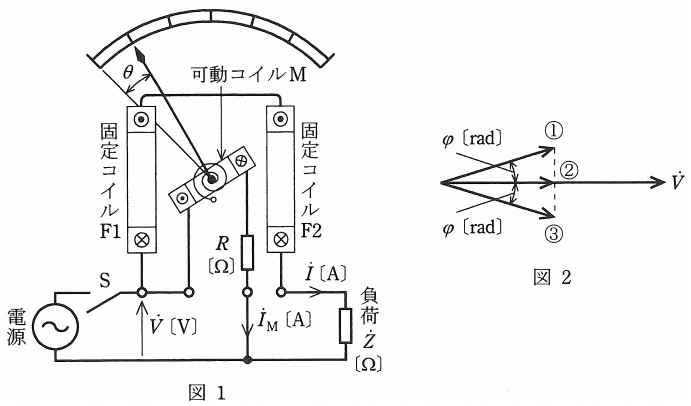
図1に示す電力計は,固定コイル\( \ \mathrm {F1} \ \),\( \ \mathrm {F2} \ \)に流れる負荷電流\( \ \dot I \ \mathrm {[A]} \ \)による磁界の強さと,可動コイル\( \ \mathrm {M} \ \)に流れる電流\( \ {\dot I}_{\mathrm {M}} \ \mathrm {[A]} \ \)の積に比例したトルクが可動コイルに生じる。したがって,指針の触れ角\( \ \theta \ \)は\( \ \fbox { (ア) } \ \)に比例する。
このような形の計器は,一般に\( \ \fbox { (イ) } \ \)計器といわれ,\( \ \fbox { (ウ) } \ \)の測定に使用される。
負荷\( \ \dot Z \ \mathrm {[\Omega ]} \ \)が誘導性の場合,電圧\( \ \dot V \ \mathrm {[V]} \ \)のベクトルを基準に負荷電流\( \ \dot I \ \mathrm {[A]} \ \)のベクトルを描くと,図2に示すベクトル①,②,③のうち\( \ \fbox { (エ) } \ \)のように表される。ただし,\( \ \varphi \ \mathrm {[rad]} \ \)は位相角である。
上記の記述中の空白箇所(ア),(イ),(ウ)及び(エ)に当てはまる組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
\[
\begin{array}{ccccc}
& (ア) & (イ) & (ウ) & (エ) \\
\hline
(1) & 負荷電力 & 電流力計形 & 交 流 & ③ \\
\hline
(2) & 電力量 & 可動コイル形 & 直 流 & ② \\
\hline
(3) & 負荷電力 & 誘導形 & 交流直流両方 & ① \\
\hline
(4) & 電力量 & 可動コイル形 & 交流直流両方 & ② \\
\hline
(5) & 負荷電力 & 電流力計形 & 交流直流両方 & ③ \\
\hline
\end{array}
\]
(b) 次の文章は,図1に示した単相電力計を\( \ 2 \ \)個使用し,三相電力を測定する\( \ 2 \ \)電力計法の理論に関する記述である。
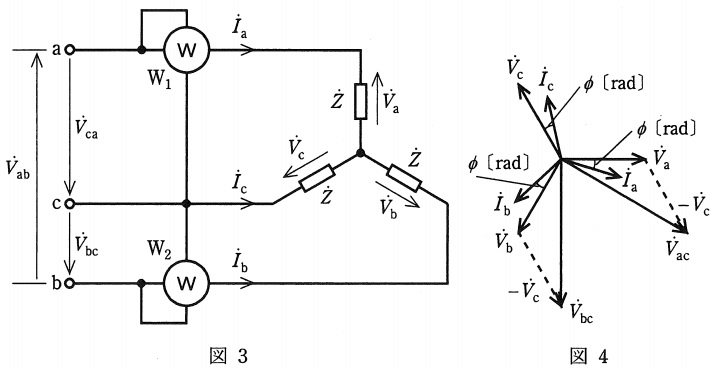
図3のように,誘導性負荷\( \ \dot Z \ \)を\( \ 3 \ \)個接続した平衡三相負荷回路に対称三相交流電源が接続されている。ここで,線間電圧を\( \ {\dot V}_{\mathrm {ab}} \ \mathrm {[V]} \ \),\( \ {\dot V}_{\mathrm {bc}} \ \mathrm {[V]} \ \),\( \ {\dot V}_{\mathrm {ca}} \ \mathrm {[V]} \ \),負荷の相電圧を\( \ {\dot V}_{\mathrm {a}} \ \mathrm {[V]} \ \),\( \ {\dot V}_{\mathrm {b}} \ \mathrm {[V]} \ \),\( \ {\dot V}_{\mathrm {c}} \ \mathrm {[V]} \ \),線電流を\( \ {\dot I}_{\mathrm {a}} \ \mathrm {[A]} \ \),\( \ {\dot I}_{\mathrm {b}} \ \mathrm {[A]} \ \),\( \ {\dot I}_{\mathrm {c}} \ \mathrm {[A]} \ \)で示す。
この回路で,図のように単相電力計\( \ \mathrm {W}_{\mathrm {1}} \ \)と\( \ \mathrm {W}_{\mathrm {2}} \ \)を接続すれば,平衡三相負荷の電力が,\( \ 2 \ \)個の単相電力計の指示の和として求めることができる。
単相電力計\( \ \mathrm {W}_{\mathrm {1}} \ \)の電圧コイルに加わる電圧\( \ {\dot V}_{\mathrm {ac}} \ \)は,図4のベクトル図から\( \ {\dot V}_{\mathrm {ac}}={\dot V}_{\mathrm {a}}-{\dot V}_{\mathrm {c}} \ \)となる。また,単相電力計\( \ \mathrm {W}_{\mathrm {2}} \ \)の電圧コイルに加わる電圧\( \ {\dot V}_{\mathrm {bc}} \ \)は\( \ {\dot V}_{\mathrm {bc}}=\fbox { (オ) } \ \)となる。
それぞれの電流コイルに流れる電流\( \ {\dot I}_{\mathrm {a}} \ \),\( \ {\dot I}_{\mathrm {b}} \ \)と電圧の関係は図4のようになる。図4における\( \ \phi \ \mathrm {[rad]} \ \)は相電圧と線電流の位相角である。
線間電圧の大きさを\( \ V_{\mathrm {ab}}=V_{\mathrm {bc}}=V_{\mathrm {ca}}=V \ \mathrm {[V]} \ \),線電流の大きさを\( \ I_{\mathrm {a}}=I_{\mathrm {b}}=I_{\mathrm {c}}=I \ \mathrm {[A]} \ \)とおくと,単相電力計\( \ \mathrm {W}_{\mathrm {1}} \ \)及び\( \ \mathrm {W}_{\mathrm {2}} \ \)の指示をそれぞれ\( \ P_{\mathrm {1}} \ \mathrm {[W]} \ \),\( \ P_{\mathrm {2}} \ \mathrm {[W]} \ \)とすれば,
\[
\begin{eqnarray}
P_{\mathrm {1}}&=&V_{\mathrm {ac}}I_{\mathrm {a}}\cos \left( \ \fbox { (カ) } \ \right) \ \mathrm {[W]} \\[ 5pt ]
P_{\mathrm {2}}&=&V_{\mathrm {bc}}I_{\mathrm {b}}\cos \left( \ \fbox { (キ) } \ \right) \ \mathrm {[W]} \\[ 5pt ]
\end{eqnarray}
\]
したがって,\( \ P_{\mathrm {1}} \ \)と\( \ P_{\mathrm {2}} \ \)の和\( \ P \ \mathrm {[W]} \ \)は,
\[
\begin{eqnarray}
P&=&P_{\mathrm {1}}+P_{\mathrm {2}}=VI \left( \ \fbox { (ク) } \ \right) \cos \phi =\sqrt {3}VI\cos \phi \ \mathrm {[W]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ 2 \ \)個の単相電力計の指示の和は三相電力に等しくなる。
上記の記述中の空白箇所(オ),(カ),(キ)及び(ク)に当てはまる組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
\[
\begin{array}{ccccc}
& (オ) & (カ) & (キ) & (ク) \\
\hline
(1) & {\dot V}_{\mathrm {b}}-{\dot V}_{\mathrm {c}} & \displaystyle \frac {\pi }{6}-\phi & \displaystyle \frac {\pi }{6}+\phi & \displaystyle 2\cos \frac {\pi }{6} \\
\hline
(2) & {\dot V}_{\mathrm {c}}-{\dot V}_{\mathrm {b}} & \displaystyle \phi -\frac {\pi }{6} & \displaystyle \phi +\frac {\pi }{6} & \displaystyle 2\sin \frac {\pi }{6} \\
\hline
(3) & {\dot V}_{\mathrm {b}}-{\dot V}_{\mathrm {c}} & \displaystyle \frac {\pi }{6}-\phi & \displaystyle \frac {\pi }{6}+\phi & \displaystyle 2\cos \frac {\pi }{3} \\
\hline
(4) & {\dot V}_{\mathrm {b}}-{\dot V}_{\mathrm {c}} & \displaystyle \frac {\pi }{3}-\phi & \displaystyle \frac {\pi }{3}+\phi & \displaystyle 2\cos \frac {\pi }{6} \\
\hline
(5) & {\dot V}_{\mathrm {c}}-{\dot V}_{\mathrm {b}} & \displaystyle \frac {\pi }{3}-\phi & \displaystyle \frac {\pi }{3}+\phi & \displaystyle 2\sin \frac {\pi }{3} \\
\hline
\end{array}
\]
【ワンポイント解説】
電力計の仕組みと二電力計法による三相電力の測定方法に関する問題です。
測定分野なので理論科目として出題される頻度としてはあまり高くない分野ですが,電力計や電力の測定方法の中では比較的出題されやすい内容と言えると思います。
1.電流力計形計器
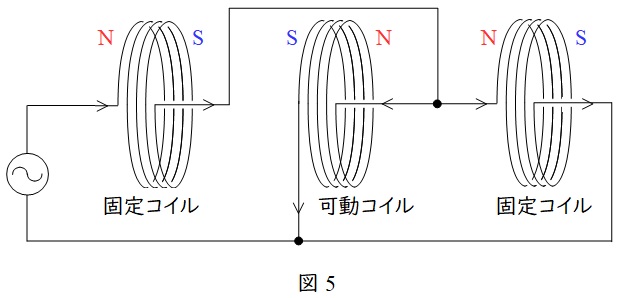
図5のように三つのコイルを配置し,中央のコイルを可動式にし,両端のコイルを固定式にします。
それぞれのコイルには右ねじの法則により磁界が発生し磁化されますが,可動コイルだけ電流を逆向きに流すことにより,それぞれに反発力が生まれます。
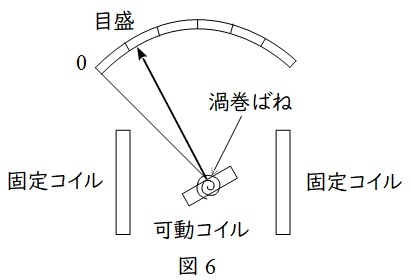
反発力の大きさが測定する電流の大きさに比例するので,図6のように可動コイルに指針をつけ軸で回転させることにより,電流の大きさや負荷電力の大きさを測定することが可能となります。また,電流がなくなった場合に元の位置に戻るように渦巻ばねが設けられています。
逆向きに流れてもすべての\( \ \mathrm {N} \ \)極と\( \ \mathrm {S} \ \)極が反転し同様の反発力が発生するため,直流・交流ともに測定可能となります。
2.二電力計法
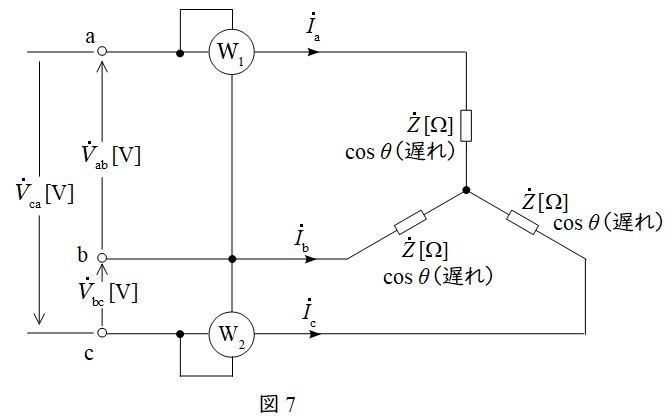
図7のように単相電力計を\( \ 2 \ \)個接続し,三相電力を測定する方法です。
電力計\( \ \mathrm {W}_{\mathrm {1}} \ \)は\( \ V_{\mathrm {ab}} \ \)と\( \ I_{\mathrm {a}} \ \)により電力を測定し,電力計\( \ \mathrm {W}_{\mathrm {2}} \ \)は\( \ V_{\mathrm {cb}} \ \)と\( \ I_{\mathrm {c}} \ \)により電力を測定します。
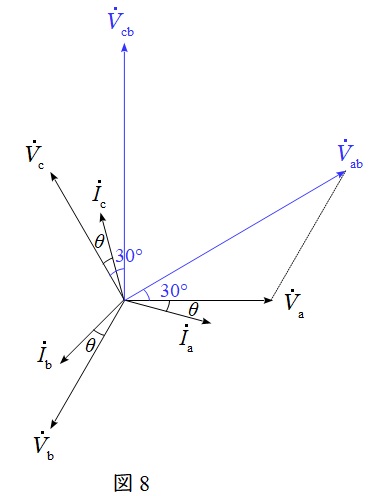
\( \ {\dot V}_{\mathrm {ab}}={\dot V}_{\mathrm {a}}-{\dot V}_{\mathrm {b}} \ \)と\( \ {\dot V}_{\mathrm {cb}}={\dot V}_{\mathrm {c}}-{\dot V}_{\mathrm {b}} \ \)はベクトル図で表すと図8のようになるため,\( \ {\dot V}_{\mathrm {ab}} \ \)と\( \ {\dot I}_{\mathrm {a}} \ \)の位相差は\( \ 30°+\theta \ \),\( \ {\dot V}_{\mathrm {cb}} \ \)と\( \ {\dot I}_{\mathrm {c}} \ \)の位相差は\( \ 30°-\theta \ \)となります。
したがって,二つの電力計\( \ \mathrm {W}_{\mathrm {1}} \ \)及び\( \ \mathrm {W}_{\mathrm {2}} \ \)が求める電力\( \ P_{\mathrm {1}} \ \)及び\( \ P_{\mathrm {2}} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {1}}&=&V_{\mathrm {ab}}I_{\mathrm {a}}\cos \left( 30°+\theta \right) \\[ 5pt ]
P_{\mathrm {2}}&=&V_{\mathrm {cb}}I_{\mathrm {c}}\cos \left( 30°-\theta \right) \\[ 5pt ]
\end{eqnarray}
\]
となります。加法定理により,上式を整理すると,
\[
\begin{eqnarray}
P_{\mathrm {1}}&=&V_{\mathrm {ab}}I_{\mathrm {a}}\left( \cos 30° \cos \theta – \sin 30° \sin \theta \right) \\[ 5pt ]
&=&V_{\mathrm {ab}}I_{\mathrm {a}}\left( \frac {\sqrt {3}}{2}\cos \theta – \frac {1}{2}\sin \theta \right) \\[ 5pt ]
P_{\mathrm {2}}&=&V_{\mathrm {cb}}I_{\mathrm {c}}\left( \cos 30° \cos \theta + \sin 30° \sin \theta \right) \\[ 5pt ]
&=&V_{\mathrm {cb}}I_{\mathrm {c}}\left( \frac {\sqrt {3}}{2}\cos \theta + \frac {1}{2}\sin \theta \right) \\[ 5pt ]
\end{eqnarray}
\]
となり,三相平衡回路である場合\( \ V_{\mathrm {ab}}=V_{\mathrm {cb}}=V \ \),\( \ I_{\mathrm {a}}=I_{\mathrm {c}}=I \ \)とおけるので,
\[
\begin{eqnarray}
P_{\mathrm {1}}&=&VI\left( \frac {\sqrt {3}}{2}\cos \theta – \frac {1}{2}\sin \theta \right) \\[ 5pt ]
P_{\mathrm {2}}&=&VI\left( \frac {\sqrt {3}}{2}\cos \theta + \frac {1}{2}\sin \theta \right) \\[ 5pt ]
\end{eqnarray}
\]
となります。上式の第\( \ 1 \ \)式と第\( \ 2 \ \)式を加えると,
\[
\begin{eqnarray}
P_{\mathrm {1}}+P_{\mathrm {2}}&=&VI\left( \frac {\sqrt {3}}{2}\cos \theta – \frac {1}{2}\sin \theta \right) +VI\left( \frac {\sqrt {3}}{2}\cos \theta + \frac {1}{2}\sin \theta \right) \\[ 5pt ]
&=&\sqrt {3}VI\cos \theta \\[ 5pt ]
\end{eqnarray}
\]
となり,三相有効電力が求められます。また,両式の差をとると,
\[
\begin{eqnarray}
P_{\mathrm {2}}-P_{\mathrm {1}}&=&VI\left( \frac {\sqrt {3}}{2}\cos \theta + \frac {1}{2}\sin \theta \right) -VI\left( \frac {\sqrt {3}}{2}\cos \theta – \frac {1}{2}\sin \theta \right) \\[ 5pt ]
&=&VI\sin \theta \\[ 5pt ]
\end{eqnarray}
\]
となることから,差をとって\( \ \sqrt {3} \ \)倍すれば三相無効電力が求められます。
【解答】
(a)解答:(5)
(ア)
ワンポイント解説「1.電流力計形計器」の通り,電力計において振れ角は負荷電流に比例した反発力がかかります。負荷電流は負荷電力に比例します。
(イ)
ワンポイント解説「1.電流力計形計器」の通り,図1のような計器を電流力計形計器と呼びます。固定コイルではなく永久磁石を用いるものを可動コイル形計器といい,直流用の計器となります。
(ウ)
ワンポイント解説「1.電流力計形計器」の通り,電流力計形計器は交流直流両方使用可能です。
(エ)
誘導性負荷の場合,電流は電圧より遅れとなるため,ベクトル図は③が正しくなります。
(b)解答:(1)
(オ)
図3及び図4より,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {bc}}&=&{\dot V}_{\mathrm {b}}-{\dot V}_{\mathrm {c}} \\[ 5pt ]
\end{eqnarray}
\]
と求められます。
※ ワンポイント解説図7と図3の\( \ \mathrm {b} \ \)相,\( \ \mathrm {c} \ \)相の位置が異なることに注意して下さい。
(カ)
図4より,\( \ {\dot V}_{\mathrm {ac}} \ \)と\( \ {\dot I}_{\mathrm {a}} \ \)の位相差は,\( \ \displaystyle \frac {\pi }{6}-\phi \ \)と求められます。
(キ)
図4より,\( \ {\dot V}_{\mathrm {bc}} \ \)と\( \ {\dot I}_{\mathrm {b}} \ \)の位相差は,\( \ \displaystyle \frac {\pi }{6}+\phi \ \)と求められます。
(ク)
(カ),(キ)とワンポイント解説「2.二電力計法」より,
\[
\begin{eqnarray}
P_{\mathrm {1}}+P_{\mathrm {2}}&=&VI\cos \left( \ \frac {\pi }{6}-\phi \ \right) +VI\cos \left( \ \frac {\pi }{6}+\phi \ \right) \\[ 5pt ]
&=&VI\left( \cos \frac {\pi }{6} \cos \phi -\sin \frac {\pi }{6} \sin \phi \right) +VI\left( \cos \frac {\pi }{6} \cos \phi +\sin \frac {\pi }{6} \sin \phi \right) \\[ 5pt ]
&=&VI\left( 2\times \cos \frac {\pi }{6} \right) \cos \phi \\[ 5pt ]
&=&\sqrt {3}VI \cos \phi \\[ 5pt ]
\end{eqnarray}
\]
と求められます。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは