《理論》〈電気及び電子計測〉[H24:問17]直流電圧計に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

直流電圧計について，次の(a)及び(b)の問に答えよ。

(a)　最大目盛\( \ 1 \ \mathrm {[V]} \ \)，内部抵抗\( \ r_{\mathrm {v}}=1000 \ \mathrm {[\Omega ]} \ \)の電圧計がある。この電圧計を用いて最大目盛\( \ 15 \ \mathrm {[V]} \ \)の電圧計とするための，倍率器の抵抗\( \ R_{\mathrm {m}} \ \mathrm {[k\Omega ]} \ \)の値として，正しいものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 12 \ \)　　(2)　\( \ 13 \ \)　　(3)　\( \ 14 \ \)　　(4)　\( \ 15 \ \)　　(5)　\( \ 16 \ \)

(b)　図のような回路で上記の最大目盛\( \ 15 \ \mathrm {[V]} \ \)の電圧計を接続して電圧を測ったときに，電圧計の指示\( \ \mathrm {[V]} \ \)はいくらになるか。最も近いものを次の(1)～(5)のうちから一つ選べ。

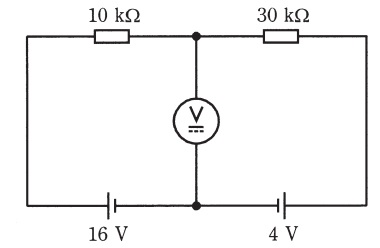
　(1)　\( \ 7.2 \ \)　　(2)　\( \ 8.7 \ \)　　(3)　\( \ 9.4 \ \)　　(4)　\( \ 11.3 \ \)　　(5)　\( \ 13.1 \ \)

【ワンポイント解説】

この問題は倍率器の内容を知って入れば，比較的容易に解ける問題ではないかと思います。(a)は倍率器の公式を忘れていても導き出せるようにしておきましょう。(b)は別解のミルマンの定理を用いると最も速く解くことができると思いますが，使用しなくても解けるため，重ね合わせの理を用いて解説しています。

1.倍率器
電圧計に直列につなぐ抵抗器のことで，電圧計の測定できる範囲を拡大することができるものです。図1のように電圧計の内部抵抗を\( \ r \ \)，倍率器の抵抗を\( \ R \ \)とすると，電圧計にかかる電圧\( \ V_{\mathrm {m}} \ \)は，分圧の法則より，
\[
\begin{eqnarray}
V_{\mathrm {m}} &=&\frac {r}{R+r}V \\[ 5pt ] \end{eqnarray}
\] となり，倍率\( \ \displaystyle m=\frac {V}{V_{\mathrm {m}}} \ \)は，
\[
\begin{eqnarray}
m&=&\frac {V}{V_{\mathrm {m}}} \\[ 5pt ] &=&\frac {R+r}{r} \\[ 5pt ] &=&1+\frac {R}{r} \\[ 5pt ] \end{eqnarray}
\] となります。よって，倍率器の抵抗の大きさは，
\[
\begin{eqnarray}
m&=&1+\frac {R}{r} \\[ 5pt ] \frac {R}{r}&=&m-1 \\[ 5pt ] R&=&\left( m-1\right) r\\[ 5pt ] \end{eqnarray}
\] と求められます。

【解答】

(a)解答：(3)
倍率\( \ m \ \)は\( \ 15 \ \)であるので，ワンポイント解説「1.倍率器」より，倍率器の抵抗\( \ R_{\mathrm {m}} \ \)の大きさは，
\[
\begin{eqnarray}
R_{\mathrm {m}}&=&\left( m-1\right) r_{\mathrm {v}} \\[ 5pt ] &=&\left( 15-1\right) \times 1000 \\[ 5pt ] &=&14000 \ \mathrm {[\Omega ]} \\[ 5pt ] &=&14 \ \mathrm {[k\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(2)
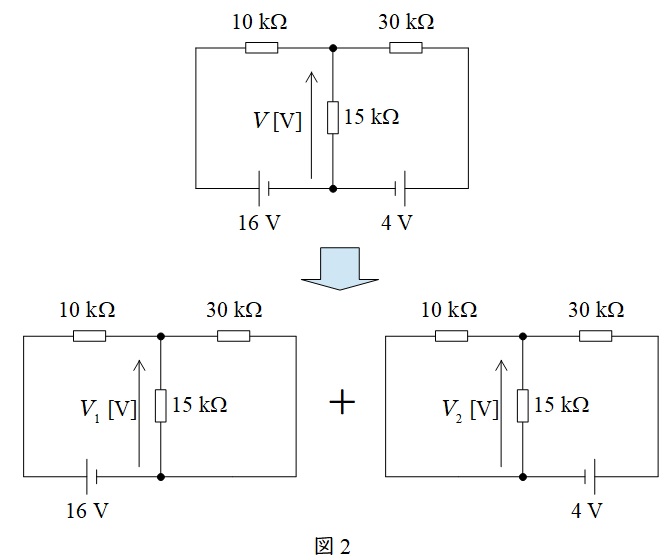
問題図の回路を重ね合わせの理を用いて分解すると，図2のようになる。
図2左の回路図より，\( \ 15 \ \mathrm {[k\Omega ]} \ \)と\( \ 30 \ \mathrm {[k\Omega ]} \ \)の合成抵抗\( \ R_{1} \ \)は，
\[
\begin{eqnarray}
R_{1}&=&\frac {15\times 30}{15+30} \\[ 5pt ] &=&10 \ \mathrm {[k\Omega ]} \\[ 5pt ] \end{eqnarray}
\] であるので，分圧の法則より，電圧計の端子電圧\( \ V_{1} \ \)は，
\[
\begin{eqnarray}
V_{1}&=&\frac {10}{10+10}\times 16 \\[ 5pt ] &=&8 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となる。次に，図2右の回路図より，\( \ 10 \ \mathrm {[k\Omega ]} \ \)と\( \ 15 \ \mathrm {[k\Omega ]} \ \)の合成抵抗\( \ R_{2} \ \)は，
\[
\begin{eqnarray}
R_{2}&=&\frac {10\times 15}{10+15} \\[ 5pt ] &=&6 \ \mathrm {[k\Omega ]} \\[ 5pt ] \end{eqnarray}
\] であるので，分圧の法則より，電圧計の端子電圧\( \ V_{2} \ \)は，
\[
\begin{eqnarray}
V_{2}&=&\frac {6}{6+30}\times 4 \\[ 5pt ] &≒&0.667 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となる。よって，求める電圧計の指示\( \ V \ \)は，
\[
\begin{eqnarray}
V&=&V_{1}+V_{2} \\[ 5pt ] &=&8+0.667 \\[ 5pt ] &≒&8.7 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

【別解】
ミルマンの定理より，電圧計の指示\( \ V \ \)は，
\[
\begin{eqnarray}
V&=&\frac {\displaystyle \frac {16}{10\times 10^{3}}+\frac {4}{30\times 10^{3}}}{\displaystyle \frac {1}{10\times 10^{3}}+\frac {1}{15\times 10^{3}}+\frac {1}{30\times 10^{3}}} \\[ 5pt ] &≒&8.7 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。