《理論》〈電気回路〉[H25:問6]抵抗で消費される電力の導出に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
- 2.1 【関連する「電気の神髄」記事】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

図の直流回路において，抵抗\( \ R=10 \ \mathrm {[\Omega ]} \ \)で消費される電力\( \ \mathrm {[W]} \ \)の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\(0.28\)　　(2)　\(1.89\)　　(3)　\(3.79\)　　(4)　\(5.36\)　　(5)　\(7.62\)

【ワンポイント解説】

重ね合わせの理もしくはテブナンの定理を用いて解くのが良いと思います。本問のように電源が２つあり，やや複雑な回路が出題された場合にはまず重ね合わせの理で解けるかを考えれば無難であると思います。

1.重ね合わせの理
複数の電源で構成された回路は，電源毎に計算した電流を重ね合わせて求めることができます。この時，電圧源は短絡，電流源は開放します。本問において回路は図1のように分解できます。

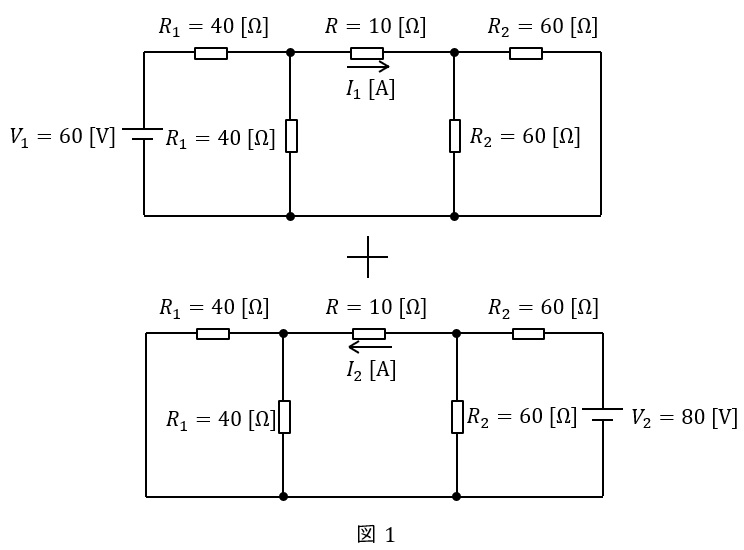
2.合成抵抗
抵抗\( \ R_{1} \ \mathrm {[\Omega ]} \ \)と\( \ R_{2} \ \mathrm {[\Omega ]} \ \)が与えられている時，それぞれの合成抵抗\( \ R \ \mathrm {[\Omega ]} \ \)は以下の式で与えられます。

①直列
直列合成抵抗\( \ R \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
R&=&R_{1}+R_{2} \\[ 5pt ] \end{eqnarray}
\] となります。

②並列
並列合成抵抗\( \ R \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
\frac {1}{R}&=&\frac {1}{R_{1}}+\frac {1}{R_{2}} \\[ 5pt ] \end{eqnarray}
\] となり，整理すると，
\[
\begin{eqnarray}
R&=&\frac {R_{1}R_{2}}{R_{1}+R_{2}} \\[ 5pt ] \end{eqnarray}
\] となります。

3.分圧・分流の法則
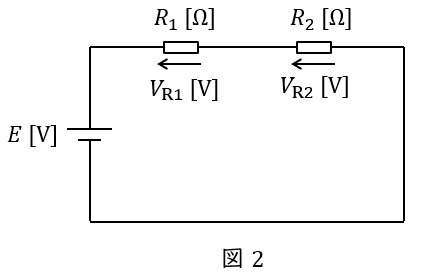
①分圧の法則
図2に示した直列回路において，各抵抗にかかる電圧は以下の通りとなります。
\[
\begin{eqnarray}
V_{\mathrm {R1}}&=&\frac {R_{1}}{R_{1}+R_{2}}E \\[ 5pt ] V_{\mathrm {R2}}&=&\frac {R_{2}}{R_{1}+R_{2}}E \\[ 5pt ] \end{eqnarray}
\]

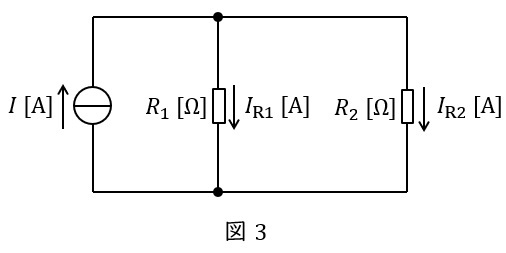
②分流の法則
図3に示した並列回路において，各抵抗に流れる電流は以下の通りとなります。分子の抵抗が分圧の法則と逆となることに注意して下さい。
\[
\begin{eqnarray}
I_{\mathrm {R1}}&=&\frac {\color{red}{R_{2}}}{R_{1}+R_{2}}I \\[ 5pt ] I_{\mathrm {R2}}&=&\frac {\color{red}{R_{1}}}{R_{1}+R_{2}}I \\[ 5pt ] \end{eqnarray}
\]

【関連する「電気の神髄」記事】

　　重ね合わせの理の証明

【解答】

解答：(1)
\( \ V_{1}=60 \ \mathrm {[V]} \ \)の電源と\( \ V_{2}=80 \ \mathrm {[V]} \ \)の電源を分けて考え，重ね合わせの理で合算する。問題図を電源毎に分解すると，図4-1及び図4-2の通りとなる。また，各部の抵抗及び電流値を図の通りとする。

図4-1より，\( \ R_{2} \ \mathrm {[\Omega ]} \ \)の二つの抵抗の並列合成抵抗\( \ R_{2}^{\prime } \ \mathrm {[\Omega ]} \ \)は，ワンポイント解説「2.合成抵抗」の通り，
\[
\begin{eqnarray}
R_{2}^{\prime }&=&\frac {R_{2}\cdot R_{2}}{R_{2}+R_{2}} \\[ 5pt ] &=&\frac {R_{2}}{2} \\[ 5pt ] &=&\frac {60}{2} \\[ 5pt ] &=&30 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となる。次に，\( \ R_{2}^{\prime } \ \mathrm {[\Omega ]} \ \)と\( \ R \ \mathrm {[\Omega ]} \ \)の直列合成抵抗\( \ R^{\prime } \ \mathrm {[\Omega ]} \ \)は，ワンポイント解説「2.合成抵抗」の通り，
\[
\begin{eqnarray}
R^{\prime }&=&R+R_{2}^{\prime } \\[ 5pt ] &=&10+30 \\[ 5pt ] &=&40 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となり，\( \ R^{\prime } \ \mathrm {[\Omega ]} \ \)と\( \ R_{1} \ \mathrm {[\Omega ]} \ \)の並列合成抵抗\( \ R_{1}^{\prime } \ \mathrm {[\Omega ]} \ \)は，ワンポイント解説「2.合成抵抗」の通り，
\[
\begin{eqnarray}
R_{1}^{\prime }&=&\frac {R^{\prime }\cdot R_{1}}{R^{\prime }+R_{1}} \\[ 5pt ] &=&\frac {40\times 40}{40+40} \\[ 5pt ] &=&20 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となり，電源\( \ V_{1} \ \mathrm {[V]} \ \)を流れる電流\( \ I_{\mathrm {v1}} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {v1}}&=&\frac {V_{1}}{R_{1}^{\prime }+R_{1}} \\[ 5pt ] &=&\frac {60}{40+20} \\[ 5pt ] &=&1 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となる。よって，抵抗\( \ R \ \mathrm {[\Omega ]} \ \)を流れる電流\( \ I_{1} \ \mathrm {[A]} \ \)は，ワンポイント解説「3.分圧・分流の法則」より，
\[
\begin{eqnarray}
I_{1}&=&\frac {R_{1}}{R^{\prime }+R_{1}}\times I_{\mathrm {v1}} \\[ 5pt ] &=&\frac {40}{40+40}\times 1 \\[ 5pt ] &=&0.5 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

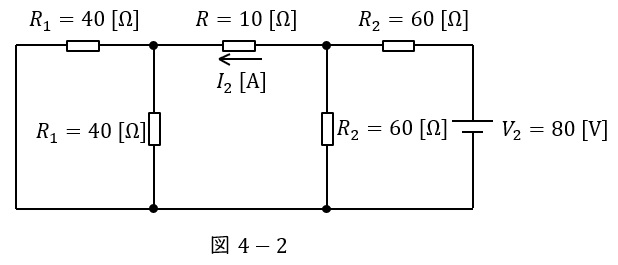
図4-1と同様に図4-2より，\( \ R_{1} \ \mathrm {[\Omega ]} \ \)の二つの抵抗の並列合成抵抗\( \ R_{1}^{\prime \prime } \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
R_{1}^{\prime \prime }&=&\frac {R_{1}\cdot R_{1}}{R_{1}+R_{1}} \\[ 5pt ] &=&\frac {R_{2}}{2} \\[ 5pt ] &=&\frac {40}{2} \\[ 5pt ] &=&20 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となる。次に，\( \ R_{1}^{\prime \prime } \ \mathrm {[\Omega ]} \ \)と\( \ R \ \mathrm {[\Omega ]} \ \)の直列合成抵抗\( \ R^{\prime \prime } \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
R^{\prime \prime }&=&R+R_{1}^{\prime \prime } \\[ 5pt ] &=&10+20 \\[ 5pt ] &=&30 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となり，\( \ R^{\prime \prime } \ \mathrm {[\Omega ]} \ \)と\( \ R_{2} \ \mathrm {[\Omega ]} \ \)の並列合成抵抗\( \ R_{2}^{\prime \prime } \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
R_{2}^{\prime \prime }&=&\frac {R^{\prime \prime }\cdot R_{2}}{R^{\prime \prime }+R_{2}} \\[ 5pt ] &=&\frac {30\times 60}{30+60} \\[ 5pt ] &=&20 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となり，電源\( \ V_{2} \ \mathrm {[V]} \ \)を流れる電流\( \ I_{\mathrm {v2}} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {v2}}&=&\frac {V_{1}}{ R_{2}^{\prime \prime }+R_{2}} \\[ 5pt ] &=&\frac {80}{20+60} \\[ 5pt ] &=&1 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となる。よって，抵抗\( \ R \ \mathrm {[\Omega ]} \ \)を流れる電流\( \ I_{2} \ \mathrm {[A]} \ \)は，ワンポイント解説「3.分圧・分流の法則」より，
\[
\begin{eqnarray}
I_{2}&=&\frac {R_{2}}{R^{\prime \prime }+R_{2}}\times I_{\mathrm {v2}} \\[ 5pt ] &=&\frac {60}{30+60}\times 1 \\[ 5pt ] &≒&0.6667 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。よって，問題図の抵抗\( \ R \ \mathrm {[\Omega ]} \ \)を流れる電流\( \ I \ \mathrm {[A]} \ \)は電流の向きに注意すると，
\[
\begin{eqnarray}
I&=&I_{2}-I_{1} \\[ 5pt ] &=&0.6667-0.5 \\[ 5pt ] &≒&0.1667 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となり，抵抗で消費される電力\( \ P \ \mathrm {[W]} \ \)は，
\[
\begin{eqnarray}
P&=&RI^{2} \\[ 5pt ] &=&10\times 0.1667^{2} \\[ 5pt ] &≒&0.2779　→　0.28 \ \mathrm {[W]} \\[ 5pt ] \end{eqnarray}
\] と求められる。