《理論》〈電気回路〉[H27:問6]直流回路の平衡条件に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

図のように，抵抗とスイッチ\(\mathrm {S}\)を接続した直流回路がある。いま，スイッチ\(\mathrm {S}\)を開閉しても回路を流れる電流\(I \ \mathrm {[A]}\)は，\(I=30 \ \mathrm {A}\)で一定であった。このとき，抵抗\(R_{4}\)の値\(\mathrm {[\Omega ]}\)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

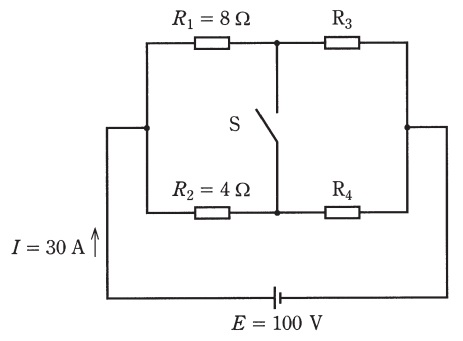
　(1)　\(0.5\)　　(2)　\(1.0\)　　(3)　\(1.5\)　　(4)　\(2.0\)　　(5)　\(2.5\)

【ワンポイント解説】

ブリッジの平衡条件と電流の分流の計算はどちらも頻出の問題です。本問を通してよく理解しておきましょう。

1.ブリッジの平衡条件
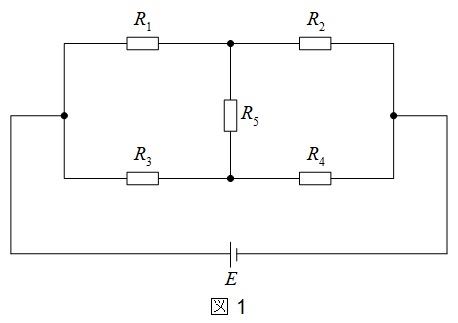
図1の回路において，ブリッジの平衡条件が成立している時，抵抗\(R_{5}\)には電流は流れません。その平衡条件は，
\[
\frac {R_{1}}{R_{2}}=\frac {R_{3}}{R_{4}}
\] もしくは，
\[
R_{1}R_{4}=R_{2}R_{3}
\] となります。

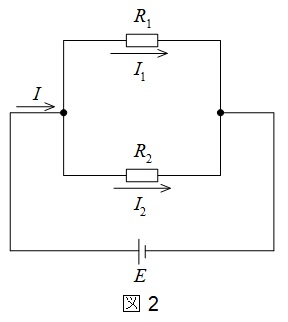
2.電流の分流の計算
図2の回路において，\(R_{1}\)と\(R_{2}\)に流れる電流\(I_{1}\)と\(I_{2}\)は，
\[
\begin{eqnarray}
I_{1}&=&\frac {R_{2}}{R_{1}+R_{2}}I \\[ 5pt ] I_{2}&=&\frac {R_{1}}{R_{1}+R_{2}}I
\end{eqnarray}
\] となります。

【関連する「電気の神髄」記事】

　　抵抗測定用ブリッジ回路まとめ

【解答】

解答：(2)
スイッチを開閉しても回路を流れる電流\(I\)に変化がないので，この回路は平衡していることが分かる。よって，ワンポイント解説「1.ブリッジの平衡条件」より，
\[
\begin{eqnarray}
\frac {R_{1}}{R_{2}}&=&\frac {R_{3}}{R_{4}} \\[ 5pt ] \frac {8}{4}&=&\frac {R_{3}}{R_{4}} \\[ 5pt ] 2&=&\frac {R_{3}}{R_{4}} \\[ 5pt ] R_{3}&=&2R_{4} \\[ 5pt ] \end{eqnarray}
\] となる。ワンポイント解説「2.電流の分流の計算」により，\(R_{2}\)及び\(R_{4}\)に流れる電流\(I_{4}\)は，
\[
\begin{eqnarray}
I_{4}&=&\frac {R_{1}+R_{3}}{\left( R_{1}+R_{3}\right) +\left( R_{2}+R_{4}\right) }I \\[ 5pt ] &=&\frac {8+2R_{4}}{\left( 8+2R_{4}\right) +\left( 4+R_{4}\right) } \times 30 \\[ 5pt ] &=&\frac {8+2R_{4}}{12+3R_{4}} \times 30 \\[ 5pt ] &=&\frac {2\left( 4+R_{4}\right) }{3\left( 4+R_{4}\right) } \times 30 \\[ 5pt ] &=&\frac {2}{3} \times 30 \\[ 5pt ] &=&20 \ \mathrm {[ A ]} \\[ 5pt ] \end{eqnarray}
\] となり，オームの法則から\(R_{4}\)は，
\[
\begin{eqnarray}
E&=&\left( R_{2}+R_{4}\right) I_{4} \\[ 5pt ] 100&=&\left( 4+R_{4}\right) \times 20 \\[ 5pt ] 4+R_{4}&=&5 \\[ 5pt ] R_{4}&=&1 \ \mathrm {[ \Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。