Contents
【問題】
【難易度】★★☆☆☆(やや易しい)
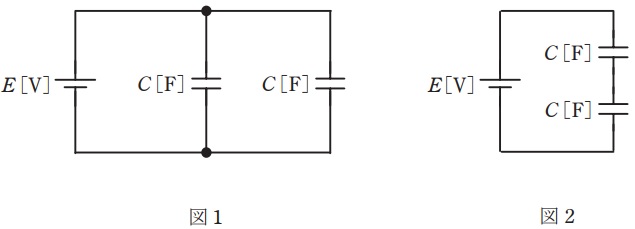
電圧\( \ E \ \mathrm {[V]} \ \)の直流電源と静電容量\( \ C \ \mathrm {[F]} \ \)の二つのコンデンサを接続した図1,図2のような二つの回路に関して,誤っているものを次の(1)~(5)のうちから一つ選べ。
(1) 図1の回路のコンデンサの合成静電容量は,図2の回路の\( \ 4 \ \)倍である。
(2) コンデンサ全体に蓄えられる電界のエネルギーは,図1の回路の方が図2の回路より大きい。
(3) 図2の回路に,さらに静電容量\( \ C \ \mathrm {[F]} \ \)のコンデンサを直列に二つ追加して,四つのコンデンサが直列になるようにすると,コンデンサ全体に蓄えられる電界のエネルギーが図1と等しくなる。
(4) 図2の回路の電源電圧を\( \ 2 \ \)倍にすると,コンデンサ全体に蓄えられる電界のエネルギーが図1の回路と等しくなる。
(5) 図1のコンデンサ一つ当たりに蓄えられる電荷は,図2のコンデンサ一つ当たりに蓄えられる電荷の\( \ 2 \ \)倍である。
【ワンポイント解説】
コンデンサを直列接続した回路と並列接続した回路の比較に関する問題です。
試験時には計算しなくても正答できるようになれるのが理想ですが,最初は解答に記載してあるように電圧がどのようになりエネルギーがどうなるかをきちんと計算して関係性をしっかりと理解するのが良いかと思います。
1.電荷\( \ Q \ \)と静電容量\( \ C \ \)及び電圧\( \ V \ \)の関係
平行平板コンデンサにおいて,蓄えられる電荷\( \ Q \ \mathrm {[C]} \ \)と静電容量\( \ C \ \mathrm {[F]} \ \)及び電圧\( \ V \ \mathrm {[V]} \ \)には,
\[
\begin{eqnarray}
Q &=&CV \\[ 5pt ]
\end{eqnarray}
\]
の関係があります。
2.コンデンサの合成静電容量
コンデンサ容量が\( \ C_{1} \ \mathrm {[F]} \ \)と\( \ C_{2} \ \mathrm {[F]} \ \)のコンデンサがある場合,直並列の合成静電容量\( \ C \ \mathrm {[F]} \ \)は下記の通りとなります。抵抗の場合と直並列が逆になることを知っておきましょう。
①並列回路の合成静電容量
\[
\begin{eqnarray}
C&=&C_{1}+C_{2} \\[ 5pt ]
\end{eqnarray}
\]
②直列回路の合成静電容量
\[
\begin{eqnarray}
\frac {1}{C}&=&\frac {1}{C_{1}}+\frac {1}{C_{2}} \\[ 5pt ]
\end{eqnarray}
\]
整理すると,
\[
\begin{eqnarray}
C&=&\frac {C_{1}C_{2}}{C_{1}+C_{2}} \\[ 5pt ]
\end{eqnarray}
\]
3.コンデンサの静電エネルギー\( \ W \ \)
コンデンサの静電エネルギー\( \ W \ \mathrm {[J]} \ \)は,コンデンサの静電容量\( \ C \ \mathrm {[F]} \ \)及びコンデンサにかかる電圧\( \ V \ \mathrm {[V]} \ \)とすると,
\[
\begin{eqnarray}
W &=&\frac {1}{2}CV^{2} \\[ 5pt ]
\end{eqnarray}
\]
であり,\( \ Q=CV \ \)の関係から,
\[
\begin{eqnarray}
W&=&\frac {1}{2}QV \\[ 5pt ]
&=&\frac {Q^{2}}{2C} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
解答:(3)
(1)正しい
ワンポイント解説「2.コンデンサの合成静電容量」の通り,図1の合成静電容量は\( \ C+C=2C \ \mathrm {[F]} \ \),図2の合成静電容量は\( \ \displaystyle \frac {C\cdot C}{C+C}=\frac {C}{2} \ \mathrm {[F]} \ \)となるので,図1のコンデンサの合成静電容量は,図2の回路の\( \ 4 \ \)倍となります。
(2)正しい
図1のコンデンサ全体に蓄えられる電界のエネルギー\( \ W_{1} \ \mathrm {[J]} \ \)は,ワンポイント解説「3.コンデンサの静電エネルギー\( \ W \ \)」の通り,
\[
\begin{eqnarray}
W_{1} &=&\frac {1}{2}CE^{2}+\frac {1}{2}CE^{2} \\[ 5pt ]
&=&CE^{2} \ \mathrm {[J]} \\[ 5pt ]
\end{eqnarray}
\]
となり,図2のコンデンサ全体に蓄えられる電界のエネルギー\( \ W_{2} \ \mathrm {[J]} \ \)は,それぞれに加わる電圧が\( \ \displaystyle \frac {E}{2} \ \mathrm {[V]} \ \)であるから,
\[
\begin{eqnarray}
W_{2} &=&\frac {1}{2}C\left( \frac {E}{2}\right) ^{2}+\frac {1}{2}C\left( \frac {E}{2}\right) ^{2} \\[ 5pt ]
&=&\frac {CE^{2}}{8}+\frac {CE^{2}}{8} \\[ 5pt ]
&=&\frac {CE^{2}}{4} \ \mathrm {[J]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,コンデンサ全体に蓄えられる電界のエネルギーは,図1の回路の方が図2の回路より大きくなります。
(3)誤り
図2の回路に,さらに静電容量\( \ C \ \mathrm {[F]} \ \)のコンデンサを直列に二つ追加すると,それぞれに加わる電圧は\( \ \displaystyle \frac {E}{4} \ \mathrm {[V]} \ \)となるので,コンデンサ全体に蓄えられる電界のエネルギー\( \ W_{2}^{\prime } \ \mathrm {[J]} \ \)は,
\[
\begin{eqnarray}
W_{2}^{\prime } &=&\frac {1}{2}C\left( \frac {E}{4}\right) ^{2}+\frac {1}{2}C\left( \frac {E}{4}\right) ^{2}+\frac {1}{2}C\left( \frac {E}{4}\right) ^{2}+\frac {1}{2}C\left( \frac {E}{4}\right) ^{2} \\[ 5pt ]
&=&\frac {CE^{2}}{32}+\frac {CE^{2}}{32}+\frac {CE^{2}}{32}+\frac {CE^{2}}{32} \\[ 5pt ]
&=&\frac {CE^{2}}{8} \ \mathrm {[J]} \\[ 5pt ]
\end{eqnarray}
\]
となり,コンデンサ全体に蓄えられるエネルギーは図1と等しくなりません。
(4)正しい
図2の回路の電源電圧を\( \ 2 \ \)倍にすると,それぞれに加わる電圧は\( \ \displaystyle E \ \mathrm {[V]} \ \)となるので,コンデンサ全体に蓄えられる電界のエネルギー\( \ W_{2}^{\prime \prime } \ \mathrm {[J]} \ \)は,
\[
\begin{eqnarray}
W_{2}^{\prime \prime } &=&\frac {1}{2}CE ^{2}+\frac {1}{2}CE^{2} \\[ 5pt ]
&=&CE^{2} \ \mathrm {[J]} \\[ 5pt ]
\end{eqnarray}
\]
となり(2)で求めた図1のコンデンサ全体に蓄えられる電界のエネルギー\( \ W_{1} \ \mathrm {[J]} \ \)と等しくなります。
(5)正しい
図1のコンデンサ一つ当たりに蓄えられる電荷\( \ Q_{1} \ \mathrm {[C]} \ \)及び図2のコンデンサ一つ当たりに蓄えられる電荷\( \ Q_{2} \ \mathrm {[C]} \ \)は,ワンポイント解説「1.電荷\( \ Q \ \)と静電容量\( \ C \ \)及び電圧\( \ V \ \)の関係」の通り,
\[
\begin{eqnarray}
Q_{1} &=&CE \\[ 5pt ]
Q_{2}&=&C\cdot \frac {1}{2}E \\[ 5pt ]
&=&\frac {1}{2}CE \\[ 5pt ]
\end{eqnarray}
\]
なので,図1のコンデンサ一つ当たりに蓄えられる電荷は,図2のコンデンサ一つ当たりに蓄えられる電荷の\( \ 2 \ \)倍となります。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは