《理論》〈電磁気〉[H28:問12]ローレンツ力に関する空欄穴埋問題

【問題】

【難易度】★☆☆☆☆（易しい）

電荷\( \ q \ \mathrm { [ C ] } \ \)をもつ荷電粒子が磁束密度\( \ B \ \mathrm { [ T ] } \ \)の中を速度\( \ v \ \mathrm { [ m/s ] } \ \)で運動するとき受ける電磁力はローレンツ力と呼ばれ，次のように導出できる。まず，荷電粒子を微小な長さ\( \ \Delta l \ \mathrm { [ m ] } \ \)をもつ線分とみなせると仮定すれば，単位長さ当たりの電荷(線電荷密度という。)は\( \ \displaystyle \frac {q}{\Delta l} \ \mathrm { [ C/m ] } \ \)となる。次に，この線分が長さ方向に速度\( \ v \ \)で動くとき，線分には電流\( \ \displaystyle I=\frac {vq}{\Delta l} \ \mathrm { [ A ] } \ \)が流れていると考えられる。そして，この微小な線電流が受ける電磁力は\( \ F=BI\Delta l \sin \theta \ \mathrm { [ N ] } \ \)であるから，ローレンツ力の式\( \ F= \ \fbox {　 （ア） 　} \ \mathrm { [ N ] } \ \) が得られる。ただし，\( \ \theta \ \)は\( \ v \ \)と\( \ B \ \)との方向がなす角である。\( \ F \ \)は\( \ v \ \)と\( \ B \ \)の両方に直交し，\( \ F \ \)の向きはフレミングの\( \ \fbox {　 （イ） 　} \ \)の法則に従う。では，真空中でローレンツ力を受ける電子の運動はどうなるだろうか。鉛直下向きの平等な磁束密度\( \ B \ \)が存在する空間に，負の電荷をもつ電子を速度\( \ v \ \)で水平方向に放つと，電子はその進行方向を前方とすれば\( \ \fbox {　 （ウ） 　} \ \)のローレンツ力を受けて\( \ \fbox {　 （エ） 　} \ \)をする。
ただし，重力の影響は無視できるものとする。

上記の記述中の空白箇所(ア)，(イ)，(ウ)及び(エ)に当てはまる組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。

\[
\begin{array}{ccccc}
& （ア） & （イ） & （ウ） & （エ） \\
\hline
(1) & qvB\sin \theta & 右　手 & 右方向 & 放物線運動 \\
\hline
(2) & qvB\sin \theta & 左　手 & 右方向 & 円運動 \\
\hline
(3) & qvB\Delta l \sin \theta & 右　手 & 左方向 & 放物線運動 \\
\hline
(4) & qvB\Delta l \sin \theta & 左　手 & 左方向 & 円運動 \\
\hline
(5) & qvB\Delta l \sin \theta & 左　手 & 右方向 & ブラウン運動 \\
\hline
\end{array}
\]

【ワンポイント解説】

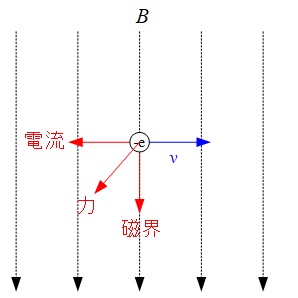
本問は電験の中でも頻出項目から出題されています。問題文の電子の運動は下図のように表されます。電子の動く向きは電流と逆になることに注意して下さい。

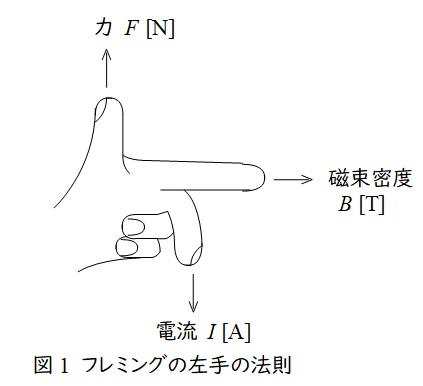
1.フレミングの左手の法則
中指を電流の向き，人差し指を磁界の向きに合わせると，親指の方向に力が働くという法則で，頭文字を取って「電磁力」と覚えます。
磁束密度の大きさ\( \ B \ \)，電流の大きさ\( \ I \ \)，直線状導体の長さを\( \ l \ \)とすると，導体に発生する電磁力\( \ F \ \)は
\[
\begin{eqnarray}
F &=&BIl \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(2)
(ア)
\(F=BI\Delta l \sin \theta \mathrm { [ N ] }\)に\(\displaystyle I=\frac {vq}{\Delta l}\mathrm { [ A ] }\)を代入すると，
\[
F=B\frac {vq}{\Delta l}\Delta l \sin \theta =qvB\sin \theta
\] と求められる。

(イ)
本問の関係は，フレミングの左手の法則に従います。

(ウ)
ワンポイント解説の通り，ローレンツ力は電子の進行方向の右方向となります。

(エ)
電子には常に進行方向に垂直の力が加わるので，円運動することになります。