《理論》〈電磁気〉[H30:問4]円形導体ループ電流による磁界の強さに関する論説問題

【問題】

【難易度】★★☆☆☆（やや易しい）

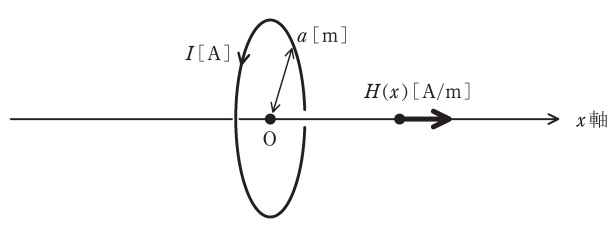
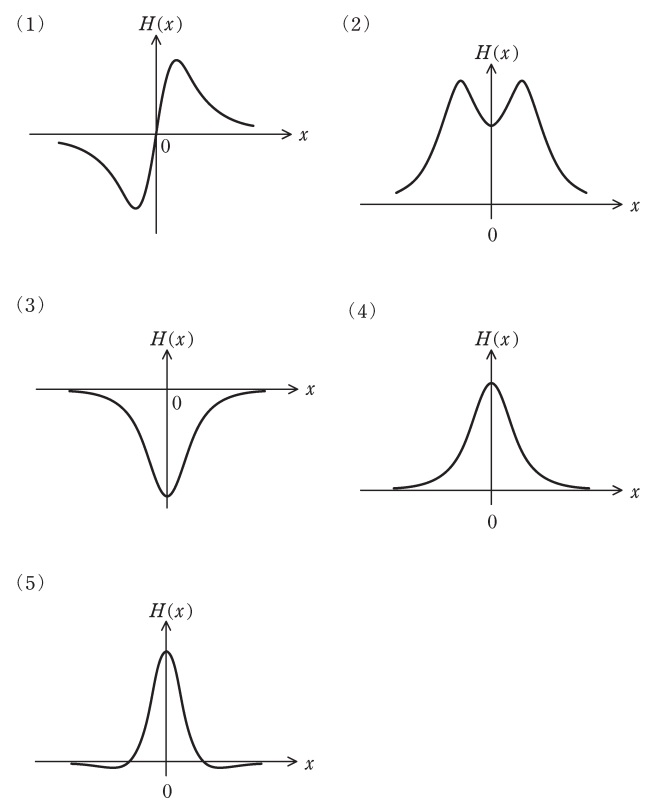
図のように，原点\(\mathrm {O}\)を中心とし\(x\)軸を中心軸とする半径\( \ a \ \mathrm {[m]} \ \)の円形導体ループに直流電流\( \ I \ \mathrm {[A]} \ \)を図の向きに流したとき，\(x\)軸上の点，つまり，\(\left( x，y，z\right) =\left( x，0，0\right) \)に生じる磁界の\(x\)方向成分\( \ H (x) \ \mathrm {[A／m]} \ \)を表すグラフとして，最も適切なものを次の(1)～(5)のうちから一つ選べ。

【ワンポイント解説】

正確に磁界の分布を求めるにはビオ・サバールの法則の理解が必要ですが，試験本番では計算は使わず，右ねじの法則で磁界の方向を特定し，距離が離れれば離れるほど小さくなるという感覚を持って解くようにして下さい。解説では一応ビオ・サバールの法則を使用し正確に導出しています。

1.ビオ・サバールの法則
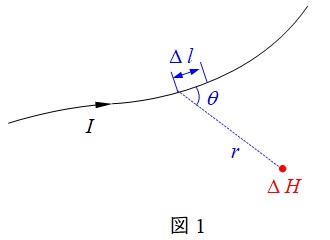
図1に示すように，微小な長さ\(\Delta l\)に流れる電流\(I\)が，距離\(r\)離れた場所に作る磁界\(\Delta H\)は，
\[
\begin{eqnarray}
\Delta H&=&\frac {I \Delta l}{4\pi r^{2}}\sin \theta \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(4)
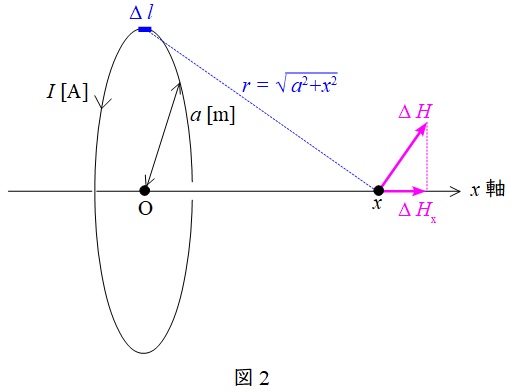
図2に示す円形電流の微小区間\(\Delta l\)による磁界\(\Delta H\)は，ワンポイント解説「ビオ・サバールの法則」より，
\[
\begin{eqnarray}
\Delta H&=&\frac {I \Delta l}{4\pi r^{2}}\sin 90° \\[ 5pt ] &=&\frac {I \Delta l}{4\pi \left( \sqrt {a^{2}+x^{2}}\right) ^{2}}\sin 90° \\[ 5pt ] &=&\frac {I }{4\pi \left( a^{2}+x^{2}\right) }\Delta l \\[ 5pt ] \end{eqnarray}
\] となる。よって，その\(x\)方向成分\(\Delta H_{\mathrm {x}}\)は，
\[
\begin{eqnarray}
\Delta H_{\mathrm {x}}&=&\Delta H \cdot \frac {a}{\sqrt {a^{2}+x^{2}}} \\[ 5pt ] &=&\frac {I }{4\pi \left( a^{2}+x^{2}\right) }\Delta l \cdot \frac {a}{\sqrt {a^{2}+x^{2}}} \\[ 5pt ] &=&\frac {Ia }{4\pi \left( a^{2}+x^{2}\right) ^{\frac {3}{2}}}\Delta l \\[ 5pt ] \end{eqnarray}
\] となる。(→補足)この\(\Delta H_{\mathrm {x}}\)の値は，円形ループ電流のどの地点においても等しい。したがって，円形ループによる磁界の\(x\)方向成分の合計\( \ H (x) \ \)は，
\[
\begin{eqnarray}
H (x)&=&\frac {Ia }{4\pi \left( a^{2}+x^{2}\right) ^{\frac {3}{2}}}\cdot 2\pi a \\[ 5pt ] &=&\frac {Ia^{2} }{2 \left( a^{2}+x^{2}\right) ^{\frac {3}{2}}} \\[ 5pt ] \end{eqnarray}
\] と求められる。\(H(x)\)の最大値は\(x=0\)の時であり，\(x\)の値が\(0\)から遠くなるほど\(H(x)\)は小さくなる。よって(4)のグラフとなる。