Contents
【問題】
【難易度】★★★☆☆(普通)
次の文章は,抵抗器の許容電力に関する記述である。
許容電力\(\displaystyle \frac {1}{4} \ \mathrm {W}\),抵抗値\(100 \ \Omega \)の抵抗器\(\mathrm {A}\),及び許容電力\(\displaystyle \frac {1}{8} \ \mathrm {W}\),抵抗値\(200 \ \Omega \)の抵抗器\(\mathrm {B}\)がある。抵抗器\(\mathrm {A}\)と抵抗器\(\mathrm {B}\)とを直列に接続したとき,この直列抵抗に流すことのできる許容電流の値は\(\fbox { (ア) } \ \mathrm {mA} \ \)である。また,直列抵抗全体に加えることのできる電圧の最大値は,抵抗器\(\mathrm {A}\)と抵抗器\(\mathrm {B}\)とを並列に接続した時に加えることのできる電圧の最大値の\(\fbox { (イ) }\)倍である。
上記の記述中の空白箇所(ア)及び(イ)に当てはまる数値の組合せとして,最も近いものを次の(1)~(5)のうちから一つ選べ。
\[
\begin{array}{ccc}
& (ア) & (イ) \\
\hline
(1) & 25.0 & 1.5 \\
\hline
(2) & 25.0 & 2.0 \\
\hline
(3) & 37.5 & 1.5 \\
\hline
(4) & 50.0 & 0.5 \\
\hline
(5) & 50.0 & 2.0 \\
\hline
\end{array}
\]
【ワンポイント解説】
こういう問題では,最初に回路図を描いて解くようにします。直列回路では各抵抗器に流れる電流が等しく,並列回路では各抵抗器に加わる電圧が等しいことを理解しておきましょう。
1.抵抗器の電力と電圧,電流の関係
抵抗値が\(R\)の抵抗に直流電圧\(V\)をかけた時,流れる電流を\(\displaystyle I= \frac {V}{R}\)とすると,抵抗の電力\(W\)は,
\[
\begin{eqnarray}
W&=&VI \\[ 5pt ]
&=&RI^{2} \\[ 5pt ]
&=&\frac {V^{2}}{R} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
解答:(1)
抵抗器\(\mathrm {A}\)の許容電流を\(I_{\mathrm {A}}\)とすると,許容電力\(\displaystyle W_{\mathrm {A}}=\frac {1}{4} \ \mathrm {W}\),抵抗値\(R_{\mathrm {A}}=100 \ \Omega \)であるから,
\[
\begin{eqnarray}
W_{\mathrm {A}}&=&R_{\mathrm {A}}I_{\mathrm {A}}^{2} \\[ 5pt ]
I_{\mathrm {A}}&=&\sqrt {\frac {W_{\mathrm {A}}}{R_{\mathrm {A}}}} \\[ 5pt ]
&=&\sqrt {\frac {\frac {1}{4}}{100}} \\[ 5pt ]
&=&\sqrt {\frac {1}{400}} \\[ 5pt ]
&=&\frac {1}{20} \\[ 5pt ]
&=&0.05 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
となる。また,抵抗器\(\mathrm {A}\)に加えることができる最大電圧\(V_{\mathrm {A}}\)は,
\[
\begin{eqnarray}
V_{\mathrm {A}}&=&R_{\mathrm {A}}I_{\mathrm {A}} \\[ 5pt ]
&=&100\times 0.05 \\[ 5pt ]
&=&5 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
となる。同様に,抵抗器\(\mathrm {B}\)の許容電流を\(I_{\mathrm {B}}\)とすると,許容電力\(\displaystyle W_{\mathrm {B}}=\frac {1}{8} \ \mathrm {W}\),抵抗値\(R_{\mathrm {B}}=200 \ \Omega \)であるから,
\[
\begin{eqnarray}
W_{\mathrm {B}}&=&R_{\mathrm {B}}I_{\mathrm {B}}^{2} \\[ 5pt ]
I_{\mathrm {B}}&=&\sqrt {\frac {W_{\mathrm {B}}}{R_{\mathrm {B}}}} \\[ 5pt ]
&=&\sqrt {\frac {\frac {1}{8}}{200}} \\[ 5pt ]
&=&\sqrt {\frac {1}{1600}} \\[ 5pt ]
&=&\frac {1}{40} \\[ 5pt ]
&=&0.025 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
となる。また,抵抗器\(\mathrm {B}\)に加えることができる最大電圧\(V_{\mathrm {B}}\)は,
\[
\begin{eqnarray}
V_{\mathrm {B}}&=&R_{\mathrm {B}}I_{\mathrm {B}} \\[ 5pt ]
&=&200\times 0.025 \\[ 5pt ]
&=&5 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
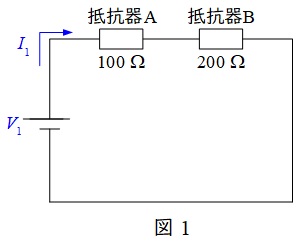
と求められる。図1において,直列抵抗に流すことのできる許容電流\(I_{1}\)は\(I_{\mathrm {A}}\)と\(I_{\mathrm {B}}\)の小さい方の値となる。よって,\(I_{1}=0.025 \ \mathrm {[A]} → 25 \ \mathrm {[mA]}\)と求められる。
この時,直列抵抗全体に加えることのできる電圧の最大値\(V_{1}\)は,
\[
\begin{eqnarray}
V_{1}&=&R_{\mathrm {A}}I_{1}+ R_{\mathrm {B}}I_{1} \\[ 5pt ]
&=&100\times 0.025 + 200\times 0.025 \\[ 5pt ]
&=&7.5 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
となる。
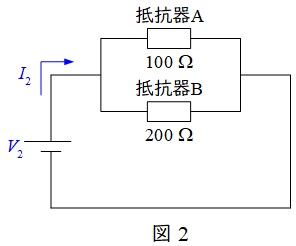
一方,並列接続したときに加えることのできる電圧の最大値\(V_{2}\)は,\(V_{\mathrm {A}}\)と\(V_{\mathrm {B}}\)の小さい方の値となる。よって,\(V_{2}=5 \ \mathrm {[V]}\)となる。
したがって,直列抵抗全体に加えることのできる電圧の最大値は,抵抗器\(\mathrm {A}\)と抵抗器\(\mathrm {B}\)とを並列に接続した時に加えることのできる電圧の最大値の\(\displaystyle \frac {7.5}{5}=1.5 \)倍と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは