Contents
【問題】
【難易度】★★☆☆☆(やや易しい)
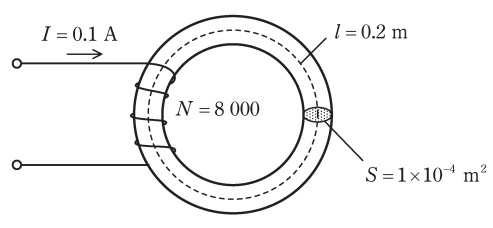
図のように,磁路の長さ\( \ l=0.2 \ \mathrm {m} \ \),断面積\( \ S=1\times 10^{-4} \ \mathrm {m^{2}} \ \)の環状鉄心に巻数\( \ N=8000 \ \)の銅線を巻いたコイルがある。このコイルに直流電流\( \ I=0.1 \ \mathrm {A} \ \)を流したとき,鉄心中の磁束密度は\( \ B=1.28\mathrm {T} \ \)であった。このときの鉄心の透磁率\( \ \mu \ \)の値\( \ \mathrm {[H/m]} \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし,コイルによって作られる磁束は,鉄心中を一様に通り,鉄心の外部に漏れないものとする。
(1) \(1.6\times 10^{-4}\) (2) \(2.0\times 10^{-4}\) (3) \(2.4\times 10^{-4}\) (4) \(2.8\times 10^{-4}\) (5) \(3.2\times 10^{-4}\)
【ワンポイント解説】
環状ソレノイドに関する問題で,定番中の定番の問題と言えると思います。本問で扱う公式はいずれも重要公式となりますので,必ず理解しておくようにしましょう。本問は断面積を与えているのが引っかけとなっています。
1.アンペアの周回積分の法則
環状ソレノイド内部において,コイルの巻数\( \ N \ \),電流\( \ I \ \),磁路の平均長\( \ l \ \)のとき,磁界の強さ\( \ H \ \)とすると,
\[
\begin{eqnarray}
NI&=&Hl \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.磁束密度\( \ B \ \)と磁界の強さ\( \ H \ \)の関係
透磁率\( \ \mu \ \)の環状ソレノイド中の磁界の強さが\( \ H \ \)であるとき,磁束密度の大きさ\( \ B \ \)は,
\[
\begin{eqnarray}
B&=&\mu H \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
解答:(5)
ワンポイント解説「1.アンペアの周回積分の法則」より,
\[
\begin{eqnarray}
NI&=&Hl \\[ 5pt ]
H&=&\frac {NI}{l} \\[ 5pt ]
\end{eqnarray}
\]
であるから,磁束密度\( \ B \ \)は,ワンポイント解説「2.磁束密度\( \ B \ \)と磁界の強さ\( \ H \ \)の関係」より,
\[
\begin{eqnarray}
B&=&\mu H \\[ 5pt ]
&=&\frac {\mu NI}{l} \\[ 5pt ]
\end{eqnarray}
\]
となる。\( \ \mu \ \)について整理し,各値を代入すると,
\[
\begin{eqnarray}
\mu &=&\frac {Bl}{NI} \\[ 5pt ]
&=&\frac {1.28\times 0.2}{8000\times 0.1} \\[ 5pt ]
&=&3.2\times 10^{-4} \ \mathrm {[H/m]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは