《理論》〈電気回路〉[R4上:問10]コンデンサに蓄えられる静電エネルギーの変化に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

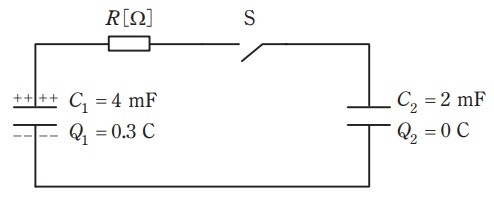
図の回路において，スイッチ\( \ \mathrm {S} \ \)が開いているとき，静電容量\( \ C_{1}=4 \ \mathrm {mF} \ \)のコンデンサには電荷\( \ Q_{1}=0.3 \ \mathrm {C} \ \)が蓄積されており，静電容量\( \ C_{2}=2 \ \mathrm {mF} \ \)のコンデンサの電荷は\( \ Q_{2}=0 \ \mathrm {C} \ \)である。この状態でスイッチ\( \ \mathrm {S} \ \)を閉じて，それから時間が十分に経過して過渡現象が終了した。この間に抵抗 \( \ R \ \mathrm {[\Omega ]} \ \)で消費された電気エネルギー\( \ \mathrm {[J]} \ \)の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 1.25 \ \)　　(2)　\( \ 2.50 \ \)　　(3)　\( \ 3.75 \ \)　　(4)　\( \ 5.63 \ \)　　(5)　\( \ 7.50 \ \)　　

【ワンポイント解説】

コンデンサ間の電荷の移動によるエネルギー変化を問う問題です。
スイッチ\( \ \mathrm {S} \ \)を閉じることで静電容量\( \ C_{1} \ \)のコンデンサに蓄えられていた電荷が静電容量\( \ C_{2} \ \)のコンデンサに移動し，最終的に両コンデンサの電圧が等しくなる状態が定常状態となります。

1.電荷\( \ Q \ \)と静電容量\( \ C \ \)及び電圧\( \ V \ \)の関係
コンデンサにおいて，蓄えられる電荷\( \ Q \ \)と静電容量\( \ C \ \)及び電圧\( \ V \ \)には，
\[
\begin{eqnarray}
Q &=&CV \\[ 5pt ] \end{eqnarray}
\] の関係があります。

2.コンデンサの静電エネルギー\( \ W \ \)
コンデンサの静電エネルギー\( \ W \ \)は，
\[
\begin{eqnarray}
W &=&\frac {1}{2}CV^{2} \\[ 5pt ] \end{eqnarray}
\] であり，\( \ Q=CV \ \)の関係から，
\[
\begin{eqnarray}
W&=&\frac {1}{2}QV \\[ 5pt ] &=&\frac {Q^{2}}{2C} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(3)
スイッチ\( \ \mathrm {S} \ \)が開いているとき，静電容量\( \ C_{1}=4 \ \mathrm {mF} \ \)のコンデンサに蓄えられている静電エネルギー\( \ W_{1} \ \mathrm {[J]} \ \)は，ワンポイント解説「2.コンデンサの静電エネルギー\( \ W \ \)」の通り，
\[
\begin{eqnarray}
W_{1}&=&\frac {Q_{1}^{2}}{2C_{1}} \\[ 5pt ] &=&\frac {0.3^{2}}{2\times 4.0\times 10^{-3}} \\[ 5pt ] &=&11.25 \ \mathrm {[J]} \\[ 5pt ] \end{eqnarray}
\] である。スイッチ\( \ \mathrm {S} \ \)を閉じると電荷が移動し，両コンデンサの電圧が等しくなるので，その時の電圧を\( \ V \ \)とする。両コンデンサに蓄えられる総電荷量は\( \ Q_{1}=0.3 \ \mathrm {C} \ \)のままであるから\( \ V \ \)の大きさは，ワンポイント解説「1.電荷\( \ Q \ \)と静電容量\( \ C \ \)及び電圧\( \ V \ \)の関係」より，
\[
\begin{eqnarray}
Q_{1}&=&C_{1}V+C_{2}V \\[ 5pt ] &=&\left( C_{1}+C_{2}\right) V \\[ 5pt ] V&=&\frac {Q_{1}}{C_{1}+C_{2}} \\[ 5pt ] &=&\frac {0.3}{4.0\times 10^{-3}+2.0\times 10^{-3}} \\[ 5pt ] &=&50 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，この時の両コンデンサの静電エネルギーの合計\( \ W_{2} \ \mathrm {[J]} \ \)は，
\[
\begin{eqnarray}
W_{2}&=&\frac {1}{2}C_{1}V^{2}+\frac {1}{2}C_{2}V^{2} \\[ 5pt ] &=&\frac {1}{2}\left( C_{1}+C_{2}\right) V^{2} \\[ 5pt ] &=&\frac {1}{2}\times \left( 4.0\times 10^{-3}+2.0\times 10^{-3}\right) \times 50^{2} \\[ 5pt ] &=&7.5 \ \mathrm {[J]} \\[ 5pt ] \end{eqnarray}
\] となり，抵抗で消費された電気エネルギー\( \ \Delta W \ \mathrm {[J]} \ \)は，
\[
\begin{eqnarray}
\Delta W &=&W_{1}-W_{2} \\[ 5pt ] &=&11.25-7.5 \\[ 5pt ] &=&3.75 \ \mathrm {[J]} \\[ 5pt ] \end{eqnarray}
\] と求められる。