《理論》〈電子理論〉[R2:問18]エミッタ接地トランジスタ増幅回路の動作特性に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

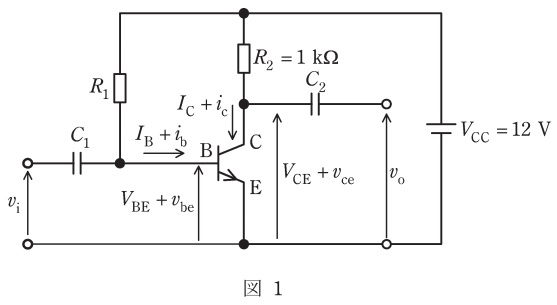
図1に示すエミッタ接地トランジスタ増幅回路について，次の(a)及び(b)の問に答えよ。

ただし，\( \ I_{\mathrm {B}} \ \mathrm {[\mu A]} \ \)，\( \ I_{\mathrm {C}} \ \mathrm {[mA]} \ \)はそれぞれベースとコレクタの直流電流であり，\( \ i_{\mathrm {b}} \ \mathrm {[\mu A]} \ \)，\( \ i_{\mathrm {c}} \ \mathrm {[mA]} \ \)はそれぞれの信号分である。また，\( \ V_{\mathrm {BE}} \ \mathrm {[V]} \ \)，\( \ V_{\mathrm {CE}} \ \mathrm {[V]} \ \)はそれぞれベース―エミッタ間とコレクタ―エミッタ間の直流電圧であり，\( \ v_{\mathrm {be}} \ \mathrm {[V]} \ \)，\( \ v_{\mathrm {ce}} \ \mathrm {[V]} \ \)はそれぞれの信号分である。さらに，\( \ v_{\mathrm {i}} \ \mathrm {[V]} \ \)，\( \ v_{\mathrm {o}} \ \mathrm {[V]} \ \)はそれぞれ信号の入力電圧と出力電圧，\( \ V_{\mathrm {CC}} \ \mathrm {[V]} \ \)はバイアス電源の直流電圧，\( \ R_{\mathrm {1}} \ \mathrm {[k\Omega ]} \ \)と\( \ R_{\mathrm {2}} \ \mathrm {[k\Omega ]} \ \)は抵抗，\( \ C_{\mathrm {1}} \ \mathrm {[F]} \ \)，\( \ C_{\mathrm {2}} \ \mathrm {[F]} \ \)はコンデンサである。なお，\( \ R_{\mathrm {2}}=1 \ \mathrm {k\Omega } \ \)であり，使用する信号周波数において\( \ C_{\mathrm {1}} \ \)，\( \ C_{\mathrm {2}} \ \)のインピーダンスは無視できるほど十分小さいものとする。

(a)　図2はトランジスタの出力特性である。トランジスタの動作点を\( \ \displaystyle V_{\mathrm {CE}}=\frac {1}{2}V_{\mathrm {CC}}=6 \ \mathrm {[V]} \ \)に選ぶとき，動作点でのベース電流\( \ I_{\mathrm {B}} \ \)の値\( \ \mathrm {[\mu A]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 20 \ \)　　(2)　\( \ 25 \ \)　　(3)　\( \ 30 \ \)　　(4)　\( \ 35 \ \)　　(5)　\( \ 40 \ \)

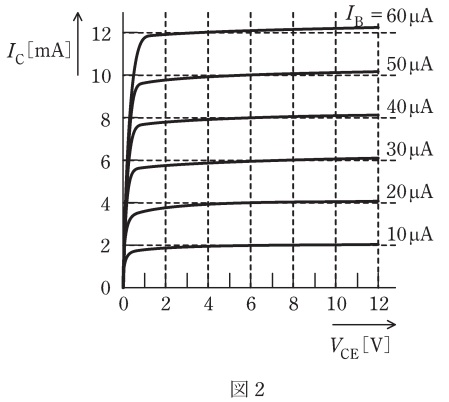
(b)　小問(a)の動作点において，図1の回路に交流信号電圧\( \ v_{\mathrm {i}} \ \)を入力すると，最大値\( \ 10 \ \mathrm {\mu A} \ \)の交流信号電流\( \ i_{\mathrm {b}} \ \)と小問(a)の直流電流\( \ I_{\mathrm {B}} \ \)の和がベース（\( \mathrm {B} \)）に流れた。このとき，図2の出力特性を使って求められる出力交流信号電圧\( \ v_{\mathrm {o}} \)（\( \ =v_{\mathrm {ce}} \ \)）の最大値\( \ \mathrm {[V]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

ただし，動作点付近においてトランジスタの出力特性は直線で近似でき，信号波形はひずまないものとする。

　(1)　\( \ 1.0 \ \)　　(2)　\( \ 1.5 \ \)　　(3)　\( \ 2.0 \ \)　　(4)　\( \ 2.5 \ \)　　(5)　\( \ 3.0 \ \)

【ワンポイント解説】

トランジスタの動作点及び出力交流信号に関する問題です。トランジスタをはじめとする電子回路の問題は，電気回路のような無数に解き方のパターンがあるわけではなく，解き方がほぼ決まっていますので，一通りマスターすると得点源になり得る分野となります。

【解答】

(a)解答：(3)
図1の回路において，直流成分について考えると，
\[
\begin{eqnarray}
V_{\mathrm {CE}}&=& V_{\mathrm {CC}}-R_{2}I_{\mathrm {C}} \\[ 5pt ] R_{2}I_{\mathrm {C}}&=& V_{\mathrm {CC}}-V_{\mathrm {CE}} \\[ 5pt ] I_{\mathrm {C}}&=&\frac { V_{\mathrm {CC}}-V_{\mathrm {CE}}}{R_{2}} \\[ 5pt ] \end{eqnarray}
\] の関係があるから，\( \ \displaystyle V_{\mathrm {CC}}=12 \ \mathrm {[V]} \ \)及び\( \ R_{\mathrm {2}}=1 \ \mathrm {k\Omega } \ \)を代入すると，
\[
\begin{eqnarray}
I_{\mathrm {C}}&=&\frac {12-V_{\mathrm {CE}}}{1} \\[ 5pt ] &=&12-V_{\mathrm {CE}} \ \mathrm {[mA]} \\[ 5pt ] \end{eqnarray}
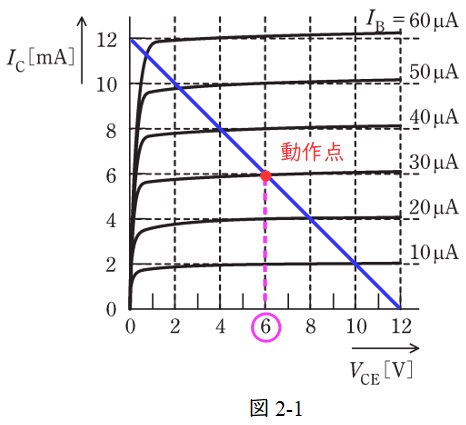
\] となる。したがって，図2に上式の一次関数のグラフを描くと図2-1のようになる。
図2-1より，\( \ \displaystyle V_{\mathrm {CE}}=\frac {1}{2}V_{\mathrm {CC}}=6 \ \mathrm {[V]} \ \)のときのベース電流\( \ I_{\mathrm {B}} \ \mathrm {[\mu A]} \ \)の値を読み取ると，\( \ I_{\mathrm {B}}=30 \ \mathrm {[\mu A]} \ \)と求められる。

(b)解答：(3)
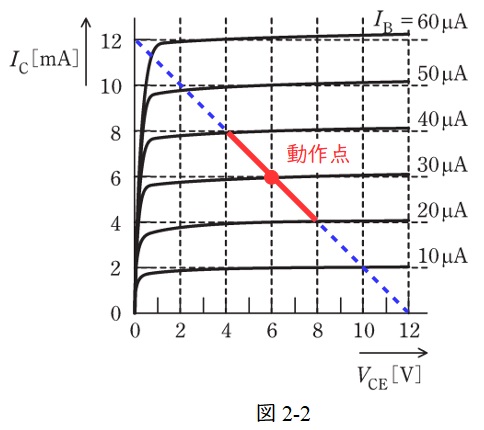
最大値\( \ 10 \ \mathrm {\mu A} \ \)の交流信号電流\( \ i_{\mathrm {b}} \ \)が流れたので，\( \ I_{\mathrm {B}}+i_{\mathrm {b}} \ \)の大きさは\( \ 20～40 \ \mathrm {\mu A} \ \)となり，動作点は図2-2の範囲を動くことになる。
したがって，出力\( \ V_{\mathrm {CE}} \ \)は\( \ 6±2 \ \mathrm {[V]} \ \)の範囲を動くことになるので，出力交流信号\( \ v_{\mathrm {o}} \ \mathrm {[V]} \ \)の最大値は\( \ 2 \ \mathrm {V} \ \)と求められる。